Lösung zu Schiefe Ebene und Gegengewicht
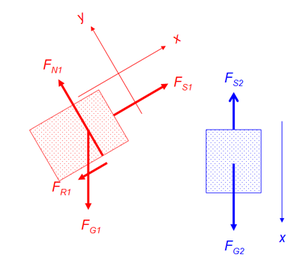
1. Auf den auf der schiefen Ebene liegenden Klotz wirken die Gewichtskraft, die Seilkraft und die beiden Komponenten der Unterlagskraft (Normalkraft und Reibungskraft). Auf das Gegengewicht wirken eine Seilkraft und eine Gewichtskraft ein. Seilkraft und Gewichtskraft auf Körper 2 sind nur dann betragsmässig gleich gross, wenn dieser Körper seinen Impulsinhalt nicht ändert, also nicht beschleunigt ist.
2. Die Impulsbilanz bezüglich der gewählten Koordinatensysteme lautet
Körper 1:
- x-Richtung: [math]F_{S1}-F_{G1}\sin(\alpha)-F_{R1}=m_1 a_1[/math]
- y-Richtung: [math]F_{N1}-F_{G1}\cos(\alpha)=0[/math]
Körper 2:
- x-Richtung: [math]F_{G2}-F_{S1}=m_2 a_2[/math]
3. Die Beschleunigung der beiden Körper wird über das Seil synchronisiert. Falls sich der Klotz wirklich in Bewegung setzt und nicht haften bleibt, ist die Gleitreibungskraft gleich Gleitreibungszahl mal Normalkraft. Dank der Idealisierung des Seilzuges sind die beiden Seilkräfte betragsmässig gleich gross. Zusammen mit der Gleichung für die Wirkung des Gravitationsfeldes (Gewichtskraft gleich Masse mal Gravitationsfeldstärke) reduziert sich das Gleichungssystem auf
- [math]F_S-m_1 g(\sin(\alpha)+\mu \cos(\alpha))=m a[/math]
- [math]g m_2-F_S=m_2 a[/math]
Löst man das System nach Beschleunigung und Seilkraft auf, erhält man
- [math]a=g\frac{m_2-m_1(\sin(\alpha)+\mu\cos(\alpha))}{m_1+m_2}[/math]=0.47 m/s2
- [math]F_S=m_2(g-a)[/math] = 39 N
4. Die Impulsänderungsraten der beiden Körper sind nur betragsmässig gleich gross. Bezüglich eines globalen Koordinatensystems zeigen die beiden Impulsänderungsraten, die resultierenden Kräfte, in verschiedene Richtungen.