Lösung zu Hubschrauber auf Waage
Der Glaskasten bildet ein geschlossenes System und die Summe über alle leitungsartigen Impulsströme (Oberflächenkräfte) plus die Stärke der Impulsquelle (Gewichtskraft) ist gleich der Änderungsrate des Impulsinhaltes. Vernachlässigt man die Impuls-Speicherfähigkeit der bewegten Luft, kann nur der Hubschrauber seinen Impulsinhalt ändern. Bezogen auf das System Glaskasten lautet die Bilanzgleichung für die Vertikalkomponente des Impulses (z-Achse gegen oben, Gravitationkraft als Impulsabfluss oder Impulssenke)
- [math]F_N - m*g = \dot p_z = m \dot v_z[/math]
FN ist die Stärke des durch die Waage fliessenden Impulsstromes (bezogen auf das System Glaskasten). Weil die Waage mit leerem Glaskasten auf Null eingestellt worden ist, steht m für die Masse des Hubschraubers. Zudem zeigt die Waage FN in Gramm an
- [math]G = \frac {F_N}{m} = m(1 + \frac {\dot v_z}{g})[/math]
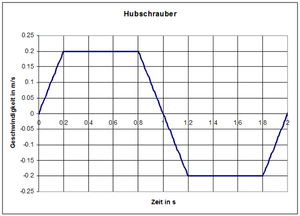
- Nach dem Start und und kurz vor der Landung zeigt die Waage mehr als 500 g an (Impulsinhalt des Hubschraubers wird grösser). Kurz vor dem Erreichen des höchsten Punktes und in der ersten Phase des Absinkens zeigt die Waage weniger als 500 g an (Hubschrauber nimmt Impuls auf).
- Dem Geschwindigkeits-Zeit-Diagramm des Hubschraubers ist zu entnehmen, wann der Impulsinhalt wie zu- oder abnimmt (das v-t-Diagramm ist das Höhen-Zeit-Diagramm im Flüssigkeitsbild). In den ersten 0.2 s und den letzten 0.2 s beträgt die Beschleunigung 1 m/s2 (0.1 g). Folglich zeigt die Waage dann 550 g an. Zwischen den Zeitpunkten 0.8 s und 1.2 s beträgt die Beschleunigung -1 m/s2 (-0.1 g) und die Waage zeigt 450 g an.