Newtonsche Axiome
Im Jahre 1687 erschien Isaac Newtons berühmtes Werk Philosophiae Naturalis Principia Mathematica (Mathematische Prinzipien der Naturphilosophie). In diesem Buch formulierte Newton drei Grundsätze (Axiome) der Bewegung, die als die Newtonschen Axiome, Newtonsche Prinzipien oder auch Newtonsche Gesetze bekannt sind. Diese drei Axiome lieferten damals, als man die Mechanik hauptsächlich mit Hilfe der euklidschen Geometrie beschreiben wollte, eine saubere Grundlage für die Punktmechanik. Wer aber heute noch in den Newtonschen Prinzipien die Grundlage der Mechanik sieht, ignoriert nicht nur hundert Jahre wissenschaftlichen Fortschritt, er verkennt auch, dass die Punktmechanik mit ihren abstrakten Begriffen wie Beschleunigung und Kraft schwer zu vermitteln ist.
Trägheitsprinzip
Die heute verwendete Formulierung des ersten Netwon'schen Axioms lautet
Jeder Körper verharrt im Zustand der Ruhe oder der gleichförmig geradlinigen Bewegung, solange keine Kraft auf ihn wirkt.
Dieses Prinzip, mit dem Newton die Erkenntnisse von Galileo Galilei bezüglich der Trägheit zusammengefasst hatte, umschreibt die kinematische Wirkung des Impulses. In der Sprache der Physik der dynamischen Systeme lautet das erste Gesetz von Newton
Jeder Körper behält seine Geschwindigkeit bei, solange er keinen Impuls mit der Umgebung austauscht.
wissenschaftliche Vorbehalte
Das Trägheitsprinzip enthält einen Zirkelschluss, den Newton nur mit der Einführung eines absoluten Raumese und einer absoluten Zeit durchbrechen konnte. Weil die Grösse der Gewichtskraft, die Stärke der gravitativen Impulsquelle, nicht direkt sondern nur indirekt entweder über die Beschleunigung oder über eine Kompensationskraft gemessen werden kann, musste Newton einen kastenförmigen Weltraum einführen, in dem eine orts- und geschwindigkeitsunabhängige Zeit ohne Rückkopplung mit dem Geschehen abläuft. Dank diesen Rahmenbedingungen lässt sich von jedem Körper sagen, ob er beschleunigt ist oder nicht, ob er absolut kräftefrei ist oder nicht.
Einstein hat das Trägheitsprinzip umgedeutet. In der allgemeinen Relativitätstheorie gibt es keine Gerade mehr, längs derer ein Körper seine Geschwindigkeit beibehalten könnte. Die zum Trägheitsprinzip äquivalente Aussage lautet heute
Die Weltlinie eines kräftefreien Körpers verläuft auf dem kürzesten Weg durch die Raum-Zeit
Unter den Begriff Kraft fallen hier alle Impulsstromstärken mit Ausnahme der gravitativen Impulsquelle (weil die Gravitation in der Krümmung der Raum-Zeit steckt, gibt es in der relativistischen Welt gar keine Gewichts-, Gravitations- oder Schwerkraft mehr im Sinne von Newton).
didaktische Vorbehalte
Das Kastenuniversum mit der überall synchron zerfliessenden Zeit deckt sich recht gut mit unseren intuitiven Vorstellungen von Raum und Zeit. Nur zerlegt das Gravitationsfeld der Erde unseren Raum in eine Ebene sowie eine Vertikale mit einem Unten und einem Oben. Weil zudem alle Körper, die sich auf einer horizontalen Ebene zwanglos bewegen, so lange Impuls mit der Erde austauschen, bis sie zur Ruhe kommen, und weil jede erzwungene Bewegung ein leistungsbehafteter Impulsaustausch mit der Erde erfordert, ist für uns die Ruhe und nicht der Bewegungszustand (Bewegung mit konstanter Geschwindigkeit) der natürliche Zustand eines Körpers.
Will man das Trägheitsprinzip an einem einfachen Beispiel erläutern, muss der Körper mechanisch gegen Erde isoliert und durch eine Führung am Fallen gehindert werden. Die Schülerinnen und Schüler können dann erkennen, dass ein Fahrzeug auf der Luftkissenbahn beliebig lang geradeaus fahren würde, wenn nicht noch ein wenig Reibung da wäre. Doch begreifen sie dann auch, dass ein zu schnelles Auto aus genau dem gleichen Grund die Kurve nicht erwischt oder ziehen sie lieber das Fehlkonzept mit der Zentrifugalkraft vor?
Verlegt man den Vorgang in den Weltraum, um sich den störenden Einflüssen der Erde zu entziehen, wird die Sache nicht einfacher. Im Innern einer antriebslosen Weltraumstation erfüllt jeder Körper das Trägheitsprinzip: der Körper schwebt an Ort oder bewegt sich gleichförmig gegen die eine Wand der Raumstation. Nun wirkt gemäss Newton aber auch auf diese Körper eine Gewichts- oder Gravitationskraft ein. Falls also eine Raumstation in nur wenigen hundert Kilometer Höhe um die Erde fällt, erfahren alle Körper eine Beschleunigung von mehr als 9 m/s2 und erfüllen dennoch gegenüber der Raumstation das Trägheitsgesetz von Newton. Wäre es nicht langsam an der Zeit, die Einstein'sche Definition des Trägheitsprinzips zu verwende, wonach alle frei fallenden Systeme lokal inertial sind?
Alternative
Die Physik der dynamischen Systeme führt den Impuls als dreifache, bilanzierfähige Primärgrösse ein. Damit wird das Trägheitsprinzip zur trivialen Aussage, wonach ein Körper seinen Impulsinhalt und damit auch seine Geschwindigkeit beibehält, solange er keinen Impuls austauscht. Der systemdynamischen Zugang zur Physik bringt die Mechanik näher an die Erfahrungswelt der Schülerinnen und Schüler heran, regt sie zu weiterem Nachdenken an und öffnet das Tor zur Physik des 20. Jahrhunderts.
Beispiele
- Will ein Schüler mit seinem Fahrrad geradeaus fahren, muss er den an die Luft abfliessenden Impuls (Luftwiderstand) von der Erde her wieder zuführen. Weil der Impuls dabei von der Erde auf die Geschwindigkeit des Fahrrades gepumpt werden muss, ist Velo fahren so anstrengend.
- Will man einen Güterwagen anhalten, muss man dessen gesamten Impulsinhalt an die Erde abführen. Dazu kann man die Bremse betätigen oder den Wagen gegen einen Prellbock fahren lassen. Da schwere Güterwagen bei gleicher Geschwindigkeit mehr Impuls speichern als leichte, stossen beladene Wagen den Prellbock eher weg als leere.
- Je schneller sich ein Körper bewegt, desto mehr Impuls pro Masse enthält er. Photonen, die nur mit Lichtgeschwindigkeit fliegen dürfen, speichern deshalb pro Masse (Energie) am meisten Impuls.
- Prallen zwei Autos frontal aufeinander, gibt das vorwärts fahrende Auto Impuls an das entgegenkommende ab, bis beide gleich schnell sind. Solche Prozesse diskutiert man am besten im Flüssigkeitsbild.
Aktionsprinzip
Das zweite Axiom, Gesetz oder Prinzip, auch Grundgesetz der Mechanik genannt, umschreibt die Wirkung der Kräfte
Wirkt auf einen Körper eine Kraft, so wird er in Richtung der Kraft beschleunigt. Die Beschleunigung ist der Kraft direkt, der Masse des Körpers umgekehrt proportional. ( F = ma )
Weil Kräfte eine Beschleunigung verursachen, nennt man dieses Axiom auch Beschleunigungsprinzip.
Das zweite Prinzip von Newton fasst zwei Gesetze der Mechanik zusammen
- Bilanzgesetz: Die Summe über alle Impulsstromstärken bezüglich eines Körpers plus die (gravitative) Impulsquelle sind gleich der Änderungsrate des Impulsinhaltes.
- Kapazitivgesetz: Der Impulsinhalt eines Körpers dividiert durch seine Masse bestimmt die Geschwindigkeit seines Massenmittelpunktes.
wissenschaftliche Vorbehalte
Das Aktionsprinzip wird häufig zur Definition der Kraft selber benutzt. Weil das Grundgesetz so einmal die Kräfte definiert und dann deren Wirkung, die Beschleunigung, beschreibt, ist der logische Zirkelschluss kaum zu vermeiden. Jeder Versuch, die Kraft unabhängig vom zweiten Axiom von Newton zu erklären, führt aber zu weiteren Widersprüchen. Deshalb kann das zweite Gesetz von Newton nur im Sinne eines Axioms verstanden werden, falls die Kräfte als nicht weiter zu erklärende Elemente der Mechanik angesehen werden oder durch ein Kraftgesetz explizit gegeben sind. Weil ein solches Gesetz nur für die Gravitationskraft formuliert werden kann, darf die Newton-Mechanik streng nenommen nur auf die Bewegung von isolierten Körpern im Vakuum (Himmelsmechanik, Wurf im Vakuum) angewendet werden.
Schnittprinzip
Die technische Mechanik hat sich schon längst von der Newtonschen Axiomatik verabschiedet. Nichtgravitative Kräfte sind reine Schnittgrössen, die an den Kontaktflächen zu andern Systemen auftreten und lokal mit Hilfe des Spannungstensors beschrieben werden können. Die (translatorische und rotatorische) Wirkung der Gravitation selber wird zu einer Ersatzkraft zusammen gefasst, die im Schwerpunkt des ausgewählten Systems angreift.
Das standartisierte Verfahren der technischen Mechanik, mit Freischneiden, Grundgesetze formulieren, geometrische Randbedingungen (Gelenke) setzen sowie dynamische Einflussgrössen (Reibung, eingeprägte Kräfte) angeben, hat sich bewährt und wird weltweit angewendet. Wer diese Vorgehensweise jedoch aus systemdynamischer Sicht analysiert, fühlt sich rasch wie im falschen Film. Da werden Querkraft- und Biegemomentenverläufe mit Hilfe einer längs des Balkens wandernden Schnittebene gesucht, obwohl diese Darstellung mit Hilfe des Strom- und Quellenkonzepts viel effizienter gefunden werden könnte.
Alternative
Ein Körper kann über die Oberfläche oder über das Gravitationsfeld Impuls mit der Umgebung austauschen. Weil der Impuls eine vektorwertige Grösse ist, haben Stromstärke und Quelle ebenfalls Vektoreigenschaft. Die Summe über alle Impulsstromstärken sowie die Stärke der Quelle ergeben die Änderungsrate des Impulsinhaltes
- [math]\sum_i \vec F_i + \vec F_G = \dot {\vec p}[/math]
Ersetzt man die Gewichtskraft durch (schwere) Masse mal die lokale Stärke des Gravitationsfeldes und den Impulsinhalt durch (träge) Masse mal Geschwindigkeit des Massenmittelpunktes erhält man das umfassend formulierte Grundgesetz der Translationsmechanik
- [math]\sum_i \vec F_i + m\vec g = m \dot {\vec v}_{MMP}[/math]
Oberflächenkräfte sind Impulsstromstärken bezüglich eines vorher ausgewählten Systems. Folglich können Oberflächenkräfte wie alle Stromstärken als Flächenintegral aus der zugehörigen Stromdichte (negativer Spannungstensor) berechnet werden. Der Umstand, dass sowohl die Gewichtskraft als auch die Impulsspeicherfähigkeit eines Körpers von der Masse abhängen, erklärt, wieso das Trägheitsprinzip einen Zirkelschluss enthält, wieso auf der rotierenden Erde eine Zentrifugalkraft sowie eine Corioliskraft eingeführt werden müssen und wieso Einstein die Gewichtskraft auf einen rein geometrischen Effekt hat reduzieren können.
Wechselwirkungsprinzip
Das dritte Axiom, Gesetz oder Prinzip macht aus jeder Kraft eine Wechselwirkung
Kräfte treten immer paarweise auf. Übt ein Körper A auf einen anderen Körper B eine Kraft aus (actio), so wirkt eine gleich grosse, aber entgegen gerichtete Kraft von Körper B auf Körper A (reactio).
Das dritte Prinzip hat Newton eingeführt, damit der Impuls auch im Zusammenhang mit der Gravitation erhalten bleibt. Aus heutiger Sicht - mit der Kenntnis des Impulses als Grundgrösse der Mechanik - liefert das Wechselwirkungsprinzip nur noch eine triviale Aussage
Überträgt ein Körper Impuls auf einen andern, ist die zugehörige Stromstärke bezogen auf den ersten Körper (Kraft auf den ersten Körper) gleich der Impulsstromstärke bezüglich des andern (Kraft auf den zweiten Körper).
didaktische Vorbehalte
Viele Autoren von Lehrbüchern der Physik meinen, das dritte Newtonsche Axiom erwähnen zu müssen, obwohl sie sich eigentlich immer nur mit der Bewegung eines einzelnen Körpers beschäftigen (was natürlich auch wieder äussert fragwürdig ist, weil dann die Erde als Impulslieferant nicht explizit in Erscheinung tritt). Entsprechend vielfältig sind denn auch die Missverständnisse bezüglich des Wechselwirkungsprinzips.
Führt man die Newton-Axiome korrekt ein und leitet daraus den Impuls als Erhaltungsgrösse ab, dürfte die Versagerquote nahe bei 100% liegen. Nur äusserst begabte Studierende können einem derart abstrakten Weg bis zur Einsicht folgen, dass jede Veränderung des Impulsinhaltes im einen Körper eine entsprechende Veränderung in einem oder mehreren andern Körpern hervorrufen muss. Zudem fehlt dieser punktmechanisch motivierten Herleitung die Idee des Impulstransportes: aus den Newtonschen Axiomen kann nur die Erhaltung nicht aber die viel umfassendere Vorstellung der Mengenartigkeit des Impulses abgeleitet werden.
Gruselkabinett
Leider haben nicht nur Schülerinnen und Schüler oder Studentinnen und Studenten Mühe mit der Newtonsche Axiomatik. Was zu diesem Thema und insbesondere zum dritten Axiom in deutschsprachigen Lehrbüchern schon alles geschrieben worden ist, dürfte eigentlich ausreichen, um die Physik als Schulfach aus den Lehrplänen der Gymnasien und Hochschulen zu streichen.
Die Fehlkonzepte bezüglich des Wechselwirkungsprinzips lassen sich in drei Gruppen einteilen
Verwechslung mit Gleichgewicht
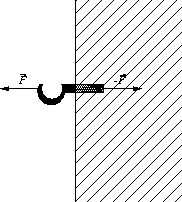
Ein Körper kann durch zwei Kräfte im Gleichgewicht gehalten werden. Weil dabei die eine Kraft entgegengesetzt gleich gross ist wie die andere, wird dieses Beispiel oft zur Erklärung des Wechselwirkungsprinzips beigezogen. Dabei macht das Wechselwirkungsprinzip eine Aussage bezüglich zweier Körper (Ein- und Austritt des Impulsstromes), wogegen sich die Gleichgewichtsbedingung auf einen einzelnen Körper bezieht. Wer das Wechselwirkungsprinzip mit Gleichgewicht verwechselt, vermischt zwei komplementäre Konzepte.
Beispiel: Ein Seil oder eine Pendelstütze stehe unter Zugspannung. Legt man die x-Achse in Richtung des Seils oder der Pendelstüze, fliesst ein x-Impulsstrom in negative Richtung. Nun zerlegt man das Seil oder die Stütze in n Teile und erhält 2n Kräfte (je zwei auf einen Teil). Je zwei Kräfte, die an der gleichen Schnittfläche auftreten aber entgegengesetzt gerichtet sind, bilden ein Wechselwirkungspaar (Actio gleich Reactio). Die zwei Kräfte, die auf das gleich Stück des Seils oder der Pendelstütze einwirken, halten dieses im Gleichgewicht. Sobald das Seil oder die Stütze beschleunigt wird, sind die einzelnen Teile nicht mehr im Gleichgewicht, das Wechselwirkungsprinzip behält dagegen seine Gültigkeit bei.
Verwechslung mit Zwangsbedingungen
Setzt man eine Tasse auf den Tisch, verformt sich dieser so lange, bis der gravitativ zugeführte Impuls unmittelbar über die Unterseite der Tasse an den Tisch abfliesst. Die Stärke des abfliessenden Impulsstromes, die Normalkraft, ist nach dem Absetzen der Tasse zwangsweise so gross wie die Gewichtskraft. Wer nun behauptet, dass infolge des dritten Newtonschen Gesetzes die Normalkraft gleich der Gewichtskraft sein müsse, sollte sich gründlich mit der Struktur der Mechanik beschäftigen oder, was bedeutend effizienter ist, die Sichtweise der Physik der dynamischen Systeme übernehmen.
Trägheitskräfte
Im deutschen Sprachraum wird leider oft noch die äusserst problematischen Trägheitskraft im Sinne von d'Alembert eingeführt. Weil damit die Dynamik auf die Statik reduziert werden kann, ist dieser Trick im Maschinenbau weit verbreitet. Bei der Anwendung des Prinzips von d'Alembert wird die Impulsänderungsrate zur negativen Trägheitskraft erklärt und auf die andere Seite der Impulsbilanz addiert. Oberflächenkräfte, Gewichts- und Trägheitskraft halten dann jeden Körper im "künstlichen" Gleichgewicht. Von der Form her unterscheidet sich die Trägheitskraft kaum von der Gewichtskraft
- [math]\vec F_G = m \vec g[/math]
- [math]\vec F_T = m \vec a_{MMP}[/math]
Das Prinzip von d'Alambert basiert demnach wie die allgemeine Relativitätstheorie auf der Ununterscheidbarkeit von schwerer und träger Masse. Nur hat die allgemeine Relativitätstheorie einen grossen Fortschritt in Bezug auf das Verständnis von Nichtinertialsystemen gebracht, wogegen das Prinzip von d'Alambert ein eigentliches Verstehen der Dynamik geradezu verhindert.
Trägheitskräfte sind Änderungsraten des Impulsinhaltes und haben folglich keinen Reaktionspartner wie die andern Kräfte (Stärken der Impulsströme und der Impulsquellen). Wer nun hingeht und anhand eines einfachen Beispiels die Trägheitskraft mit der einwirkenden Oberflächenkraft zu einem Wechselwirkungspaar zusammen fasst, ist derart bescheuert, dass ihm kaum zu helfen ist. Und dennoch sind solche Weisheiten auch schon in Lehrbüchern gedruckt worden.
Literatur
Anhand der nachfolgenden Quellen kann sich jeder selber ein Bild von den desolaten Zuständen in bekannten Lehrbüchern machen
- H. Lindner: Physik für Ingenieure Vieweg 1989 (Gleichgewicht als Spezialfall des Wechselwirkungsprinzips)
- E. Grimsehl: Lehrbuch der Physik Teubner 1957 (bei einer gleichmässig beschleunigten Bewegung sind Trägheitskraft und wirkende Kraft einander gleich, aber entgegengesetzt gerichtet)
- F. Heywang, H. Schmiedel, J. Süss: Physik für technische Berufe Handwerk und Technik 1980 (die Gegenkraft baut sich erst mit der Verformung einer Feder oder der Unterlage auf)