Hüpfender Tennisball
Ein Tennisball wird aus einer bestimmten Höhe über einem Betonboden losgelassen. Die nachfolgende Bewegung soll mit Hilfe eines eindimensionalen Modells simuliert werden.
Spezifikation

Die Tennisregeln der International Tennis Federation (ITF) schreiben für Bälle folgendes vor:
- Die äussere Hülle des Balles muss gleichförmig und nahtlos, seine Farbe weiss oder gelb sein.
- Der Ball muss diesen Anforderungen entsprechen und eine Masse von mehr als 56,7 g und weniger als 58,5 g aufweisen.
- Der Durchmesser muss mehr als 6,35 cm und weniger als 6,67 cm betragen.
- Es gibt mehrere spezifizierte Ballarten. Jeder Ball muss eine Sprunghöhe von mehr als 134,62 cm und weniger als 147,32 cm aufweisen, wenn er aus einer Höhe von 254 cm auf eine ebene, harte Fläche, z. B. Beton, fallen gelassen wird.
Aus diesen Regeln werden folgende Spezifikationen abgeleitet
- Masse 0.058 kg
- Radius 0.0325 m
- Widerstandsbeiwert 0.4
- Stosszahl 0.55
Modell
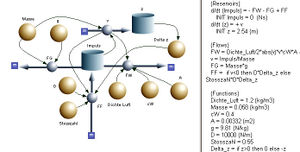
Die Impulsbilanz bildet das Rückgrat dieses Modells zur eindimensionalen Translationsmechanik. Die positive Richtung zeige nach oben. Deshalb entzieht das Gravitationsfeld der Kugel mit der konstanten Rate FG = m*g Impuls. Die Luft entzieht der Kugel mit zunehmender Geschwindigkeit immer mehr Impuls. Ist die Geschwindigkeit negativ, führt sie Impuls zu. Um dieses Verhalten sauber zu modellieren, formulieren wir den Luftwiderstand mit dem Produkt aus der Geschwindigkeit und ihrem Betrag
- [math]F_W=\frac{\varrho_L}{2}c_WA\left|v\right|v[/math]
Der statische Auftrieb, der auch in Luft wirkt, ist hier nicht berücksichtigt bzw. mit der Masse des Balls verrechnet worden.
Die Geschwindigkeit eines Körper ist dynamisch durch den Quotienten aus Impuls und Masse festgelegt. Weil die Geschwindigkeit kinematisch als Änderungsrate des Ortes definiert ist, kann die Strecke mittels einer "Rohr-Topf-Anordnung" berechnet werden. In diesem Fall muss das Rohr (flow) in den Topf (Reservoir) hinein orientiert sein. Weil die positive Richtung nach oben zeigt, nimmt auch die Höhe bis zum Aufschlag ab.
Um den Aufschlag zu modellieren, wird zuerst eine positive Strecke (Delta_z)
- Delta_z = if z>0 then 0 else -z
Die eigentliche Aufschlagdynamik basiert auf einer starken Feder, deren Federkonstante beim Entspannen um die Stosszahl kleiner ist als beim Zusammendrücken
- FF = if v<0 then D*Delta_z else Stosszahl*D*Delta_z
Simulation

Würde man den Tennisball im Vakuum fallen lassen, wäre die Beschleunigung betragsmässig gleich der Gravitationsfeldstärke. Die Geschwindigkeit des Balls würde jede Sekunde um 9.81 m/s abnehmen. Seine Endgeschwindigkeit wäre dann bei einer Fallhöhe von 2.54 m gleich
- [math]v_e=\sqrt{2gh}[/math] = 7.06 m/s
was eine Fallzeit von
- [math]t=\frac{v_e}{g}[/math] = 0.7196 s
ergibt. Die Simulation ergibt eine Endgeschwindigkeit von knapp 6.96 m/s bei einer Fallzeit von 0.724 s. Der Unterschied rührt von der Wirkung des Luftwiderstandes.
Weil der Boden als harte, teilelastische Feder (Federkonstante 10 kN/m) modelliert worden ist, muss der Zeitschritt der Simulation sehr klein gewählt werden. Nimmt man einen Zeitschritt von 10 Millisekunden (0.00001 s), müssen 500'000 Schritte ausgeführt werden, wozu ein Laptop aus dem Jahre 2007 0.28 Sekunden benötigt.
Boden modellieren
