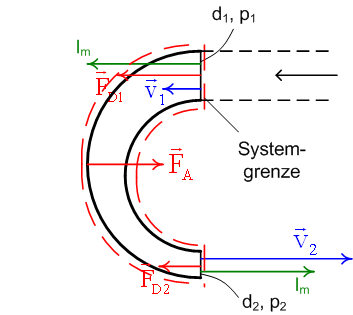
Lösung zu Kraft auf Rohrstück

Bei dieser Problemstellung sollte man sowohl beim Aufstellen der Energiebilanz als auch bei der Impulsbilanz mit dem Ueberdruck p_e arbeiten.

1. Die Energiebilanz, das Gesetz von Bernoulli, liefert zusammen mit der Kontinuitätsgleichung

[math]p_1 + \frac {\rho}{2} v_1^2 = p_2 + \frac {\rho}{2} v_2^2, \quad v_1 A_1 = v_2 A_2, \quad v_1 = v_2 \cdot \frac {d_2^2}{d_1^2}[/math]

den Eintrittsdruck, wobei p₂ = p_L = 10⁵ Pa den Luftdruck und p_e = p₁ - p₂ den Ueberdruck beim Eintritt darstellt

[math]p_e = p_1 - p_2 = \frac {\rho}{2} \left(1 - \left(\frac {d_2}{d_1}\right)^4 \right) v_2^2[/math] = 46.9 kPa

2. Die Impulsbilanz verlangt, dass sich die Festhaltekraft, die Überdruckkraft beim Eintritt und die beiden konvektiven Impulsströme zu Null addieren, weil der Impulsinhalt des Rohrstückes keine Änderung erfährt. Die Impulsbilanz wenden wir auf das System Rohrstück plus Wasser an:

[math]F_A - (p_1 - p_L) A_1 - (p_2 - p_L) A_2 + \left(- v_1 \right) \cdot I_m + v_2 \cdot \left( -I_m\right) = \dot p = 0[/math]

Bei der Ein- und Austrittsfläche berechnen wir die Druckkraft nur mit dem Ueberdruck. Wenn auf der ganzen Systemgrenze nur der überall gleiche Umgebungsdruck (also der Luftdruck) herrschen würde, hätten wir eine Nettokraft von 0. Diese Kräfte können wir also in der Impulsbilanz weglassen. Wir müssen nur das berücksichtigen, was darüber hinausgeht: die mit dem Überdruck berechneten Druckkräfte bei Ein- und Austritt und die Haltekraft F_A auf das Rohr.

[math]F_A = p_e A_1 + \left(v_1 + v_2\right) I_m = p_e A_1 + \rho v_2 \left(\left(\frac {d_2}{d_1}\right)^2 + 1 \right) I_V[/math] = 368.2 N + 49.1 N + 196.3 N = 613.6 N

Der Massenstrom [math]I_m = \rho I_V = \rho A v[/math] hat eine Stärke von 19.63 kg/s.

Aufgabe