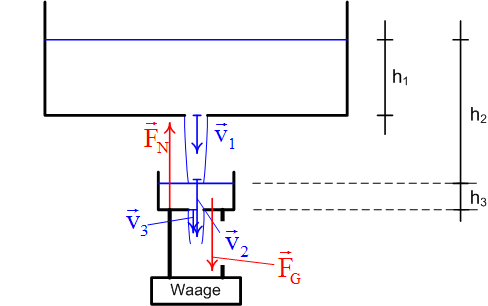
Lösung zu Abfüllwaage

ohne Loch im Becherglas

Die Impulsbilanz bezüglich des Systems Becherglas lautet (positive Richtung nach unten)

[math]{-}F_N + F_G + I_{p1} = 0[/math]

Die Stärke des konvektiven Impulsstromes I_p1 ist gleich

[math]I_{p1} = \rho v_2 I_{V1} = \rho v_2 v_1 A_1 [/math]

Die Geschwindigkeiten beim Ausfluss v₁ und beim Auftreffen auf die Wasseroberfläche v₂ ergeben sich aus der Energiebilanz (Torricelli)

[math] v_1 = \sqrt{2gh_1}, \quad v_2 = \sqrt{2gh_2}[/math]

also gilt für den konvektiven Impulsstrom

[math]I_{p1} = 2 g \rho A_1 \sqrt{h_1 h_2}[/math] = 7.29 N

Bei einer Gewichtskraft von total 35.0 N hat die Normalkraft (entspricht der Waagenanzeige) einen momentanen Wert von

[math]F_N = F_G + I_{p1}[/math] = 42.3 N

mit Loch im Becherglas

Die Volumenströme I_V1 und I_V2 sind gleich gross weil der Wasserspiegel im Becherglas auf konstanter Höhe bleibt. Die Geschwindigkeit v₃ im Loch des Becherglases beträgt: [math] v_3 = \sqrt{2gh_3}[/math]. Daraus kann man die Stärke des zweiten konvektiven Impulsstromes im Boden des Becherglases berechnen:

[math]I_{p2} = \rho v_3 I_{V2} = \rho \sqrt{2gh_3} I_{V1} = 2 \rho g \sqrt{h_3 h_1} A_1[/math] = 2.8 N

Aus der Impulsbilanz [math]{-}F_N + F_G + I_{p1} - I_{p2} = 0[/math] erhält man wieder die Festhaltekraft (oder Normalkraft)

[math]F_N = F_G + I_{p1} - I_{p2}[/math] = 39.5 N

Aufgabe