Räuber-Beute-Modell

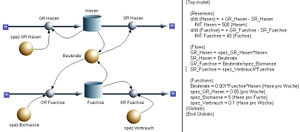
Das Räuber-Beute-Modell ist ein recht einfaches Beispiel aus der Populationsdynamik. Das Modell zeigt ein einfaches zeitliches Muster:

Je mehr Beutetiere vorhanden sind, desto mehr Räuber (Prädatoren) finden Nahrung. Die Population der Räuber nimmt daher zu.
Durch die Vernichtung der Beutetiere sinkt auf Grund der fehlenden Nahrung die Anzahl der Räuber.

Zwischen Räuber und Beutetier entwickelt sich ein dynamisches Gleichgewicht. In der Natur stimmen Räuber und Beute ihr Verhalten immer stärker aufeinander ab, was im Modell nur durch eine Anpassung der Parameter nachvollzogen werden kann.

Die dynamischen Eigenschaften von Räuber-Beute-Beziehungen werden in der theoretischen Biologie mittels verschiedenen Variationen des Grundmodells untersucht. Am bekanntesten sind die Arbeiten des österreichischen Mathematikers Alfred James Lotka und des italienischen Mathematikers und Physikers Vito Volterra, die 1925 und 1926 unabhängig voneinander die heute nach ihnen benannten Lotka-Volterra-Gleichungen formulierten. Dieses System mit zwei nichtlinearen Differentialgleichungen stellt den quantitativen Aspekt der Populationsentwicklung unter interspezifischer Konkurrenz dar.

Schneehasen und Luchse

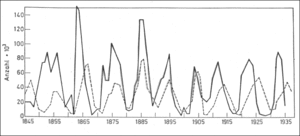
Aufzeichnungen der Hudson-Bay-Company über den Eingang der Felle von Luchsen und Schneehasen zeigen regelmässige Schwankungen mit einer Periode von 6.9 Jahren. Wir entwickeln nun ein Modell eines Räuber-Beute-Systems, das solche Schwankungen erzeugt. Zunächst betrachten wir die beiden Populationen von Füchsen und Hasen getrennt. Als Zeiteinheit wird hier die Woche genommen. Der Bestand an Füchsen vergrössert sich mit der Zufuhr von Futter (Hasen) und verringert sich entsprechend dem Energieverlust zur Erhaltung der Lebensvorgänge. Dieser Erhaltungsbedarf ist hier mit 0.1 pro Woche angesetzt, d.h. ohne Nahrungszufuhr würde ein Fuchs pro Woche 10% seines Energievorrats verlieren. Im stationären Zustand entspricht die Nahrungszufuhr dieser Menge. Bezüglich der Hasen gehen wir von einer Verdopplung der Population in 20 Wochen aus, was einer spezifischen Zuwachsrate von etwa 0.05 pro Woche entspricht.

Je mehr Hasen es gibt, desto mehr Tiere stehen den Füchsen als Beute zur Verfügung. Je mehr Füchse es gibt, desto mehr Hasen werden den Füchsen zum Opfer fallen. Das Produkt aus Hasen und Füchsen kann daher als Mass dafür genommen werden, wie viele Hasen von den Füchsen gefressen werden. Jeder erlegte Hase bringt dem Fuchsbestand einen entsprechenden Gewinn und dem Hasenbestand einen Verlust. Der zugehörige Faktoren von 5 Hasen pro Fuchs ist anhand folgender Überlegungen bestimmt worden: bei einer mittleren Zahl von 500 Hasen und 50 Füchsen sollen die Füchse ihre Verluste von 50*0.1 = 5 ersetzen können. Wird nun angenommen, dass ein Fuchs die Biomasse von 5 Hasen hat, so entspricht der Gewinn von 5 Fuchseinheiten einem Verlust von 25 Hasen. Nun werfen die 500 Hasen mit der angenommenen Fruchtbarkeit gerade 25 Junge pro Woche. Damit bleibt das System stabil.

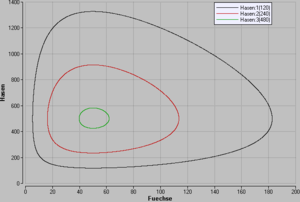
Im Phasendiagramm verlaufen alle Prozesse entsprechend den gewählten Anfangsbedingungen auf geschlossenen Bahnen um den Gleichgewichtspunkt von 50 Füchsen und 500 Hasen. Startet man mit nur 200 Hasen und 40 Füchsen, steigt die Hasenpopulation auf gegen 1400 Tiere an. Sind aber am Anfang mehr Hasen vorhanden, überschwingt der Bestand entsprechend weniger. Bei einem Startwert von 480 Hasen vermag deren Bestand nicht einmal die 600er Marke zu überschreiten.

Die Lotka-Volterra-Gleichung, welche diese Räuber-Beute-Modell beschreibt, lässt sich mathematisch gut analysieren. Schreiben wir dazu das Gleichungssystem etwas kompakter

[math]\dot H=k_1H-k_{12}HF=H(k_1-k_{12}F)[/math]

[math]\dot F=k_{21}HF-k_2F=F(k_{21}H-k_2)[/math]

Das System bleibt stabil, falls beide Änderungsraten gleich Null sind. Aus dieser Gleichung folgt für die stabile Zahl von Hasen und Füchsen

[math]H_s=\frac{k_2}{k_{21}}[/math] und [math]F_s=\frac{k_1}{k_{12}}[/math]

Dividiert man die Hasengleichung durch die Fuchsgleichung, folgt eine zeitfreie Darstellung, die sich gut separieren lässt. Ein beidseitig Integration liefert dann

[math]k_{21}(H-H_0)+k_{12}(F-F_0)-k_2\ln\frac{H}{H_0}-k_1\ln\frac{F}{F_0}=0[/math]

Futterbegrenzung

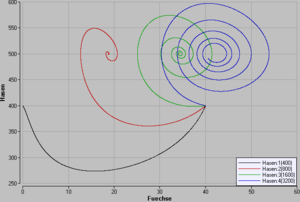
Steuert man die Geburtenrate der Hasen zusätzlich mit einer Futtergrenze (maximale Zahl von Hasen), ändert sich die Dynamik des Modells signifikant. Zur Modifikation des Modells multipliziert man die Geburtenrate mit dem spezifischen Zuwachspotenzial der Hasen

[math]spezZuwachspot=\frac{H_{max}-H}{H_{max}}[/math]

Liegt die Futtergrenze unterhalb der weiter oben bestimmten, stationären Hasenpopulation, sterben die Füchse aus. Ansonsten streben beide Populationen gegen einen Gleichgewichtszustand. Mit zunehmender Futtergrenze erträgt das System bei konstant bleibendem Mittelwert der Zahl von Hasen mehr Füchse. Gleichzeitig nehmen die Populatinsschwankungen wieder zu. Bei einer beliebig hohen Futtergrenze, erhalten wir wieder das nicht gedämpfte System mit 50 Füchsen bei 500 Hasen und einem Zyklus, der vom Anfangsbestand abhängt.