Lösung zu Vollelastischer Stoss

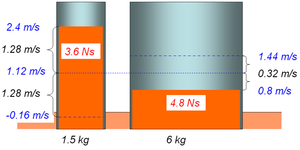
Beim total inelastischen Stoss gleicht sich die "Füllhöhe" aus [math]v_{in} = \frac{m_1 v_1 + m_2 v_2}{m_1 + m_2} = \frac{1.5 kg * 2.4 m/s + 6 kg * 0.8 m/s}{7.5 kg} = 1.12 m/s[/math]
Beim vollständig elastischen Stoss fliesst in der zweiten Stossphase, d.h. nachdem beide Geschwindigkeiten gleich gross geworden sind, nochmals so viel Impuls aus dem ersten Fahrzeug hinaus und wird im zweiten Fahrzeug hinaufgepumpt, wie vorher in der ersten Stossphase bereits geflossen ist. In der ersten Stossphase nimmt die Geschwindigkeit des ersten Fahrzeugs um 2.4 m/s - 1.12 m/s = 1.28 m/s ab. Folglich nimmt die Geschwindigkeit in der zweiten Stossphase nochmals um soviel auf 1.12 m/s - 1.28 m/s = -0.16 m/s ab, bis die Fahrzeuge auseinander fahren. Die Geschwindigkeit nimmt im zweiten Fahrzeug analog dazu von 0.8 m/s auf 1.12 m/s und dann nochmals um 0.32 m/s auf 1.44 m/s zu.