Aviatik 2015/2: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) |
||
| Zeile 32: | Zeile 32: | ||
#Für die isentrope Kompression von 2.9 bar auf 10.1 bar nehmen wir ersatzweise 10 mol ideales Gas mit einem Isentropenexponent von 1.13. Wie hoch würde die Temperatur des idealen Gases dabei steigen? |
#Für die isentrope Kompression von 2.9 bar auf 10.1 bar nehmen wir ersatzweise 10 mol ideales Gas mit einem Isentropenexponent von 1.13. Wie hoch würde die Temperatur des idealen Gases dabei steigen? |
||
#Wie gross wäre die Kompressionsarbeit für dieses Ersatzgas unter den gegebenen Bedingungen? |
#Wie gross wäre die Kompressionsarbeit für dieses Ersatzgas unter den gegebenen Bedingungen? |
||
[[Datei:Kaltdampfprozess T-s.gif|''T-S-''Diagramm]] |
|||
==Aufgabe 5== |
==Aufgabe 5== |
||
Version vom 23. Juni 2016, 11:14 Uhr
Studiengang Aviatik der ZHAW
Erlaubte Hilfsmittel: : Netzunabhängiger und nicht kommunikationsfähiger Taschenrechner, selbst verfasste Formel-, Modell- und Beispielsammlung mit maximal 14 Seiten (14 einseitig oder 7 zweiseitig beschriebene Blätter), Wörterbuch für fremdsprachige Studierende.
Daten:
- universelle Gaskonstante = 8.314 J/(mol.K)
Aufgabe 1
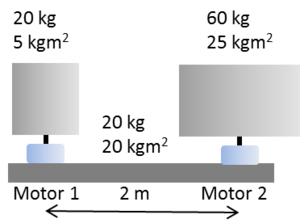
Ein Satellit besteht aus zwei zylinderförmigen Körpern (Körper 1: Masse 20 kg, Massenträgheitsmoment 5 kgm2; Körper 2: Masse 60 kg, Massenträgheitsmoment 25 kgm2) und einem Verbindungsstück (Masse 20 kg, Massenträgheitsmoment 20 kgm2). Die beiden Zylinderachsen sind parallel ausgerichtet und um zwei Meter versetzt (siehe Skizze). Der Massenmittelpunkt des Verbindungsstücks liegt genau in der Mitte zwischen den beiden Zylinderachsen. Auf den Achsen der beiden Zylinder befinden sich zwei kompakte Elektromotoren mit vernachlässigbaren Massen. Der Satellit rotiert anfänglich nicht (relativ zum Fixsternenhimmel), die Massenträgheitsmomente der drei Körper sind auf den entsprechenden Massenmittelpunkt bezogen.
- Wie weit ist der Gesamtmassenmittelpunkt von der Achse des kleineren Zylinders entfernt?
- Der Motor 1 wirkt nun während 60 Sekunden mit einem konstanten Drehmoment von 4 Nm auf den ersten Zylinder und das Verbindungsstück ein. Motor 2 wirkt gleichzeitig so auf den zweiten Zylinder ein, dass sich das Verbindungstück nicht dreht. Mit welchen Winkelgeschwindigkeiten drehen sich die beiden Zylinder nach diesen 60 Sekunden?
- Wie gross ist die Maximalleistung von Motor 2 und wie viel Energie muss er insgesamt abgeben?
- Nun nehmen wir an, dass Körper 2 fest (nicht drehbar) mit dem Verbindungsstück verbunden ist, während Motor 1 wieder während 60 Sekunden mit 4 Nm einwirkt. Mit welcher Winkelgeschwindigkeit dreht sich nachher das Verbindungsstück?
Aufgabe 2
Ein Flugzeug startet auf einer horizontal ausgerichteten Betonpiste. Kurz nach dem Start misst man bei einer Geschwindigkeit von 1.6 m/s eine Beschleunigung von 2 m/s2. Das Flugzeug wirkt mit 4 kN vertikal auf die Achse des Bugrades ein (Masse 30 kg, Radius 0.4 m, Massenträgheitsmoment 12 kgm2). Das Bugrad rollt ohne zu rutschen und wir vernach¬lässigen jegliche Dissipation (Lagerreibung, Rollreibung, Gleitreibung).
- Wie gross ist die Schnelligkeit (Betrag der Geschwindigkeit) am vordersten Punkt des Rades (auf dem Umfang auf Höhe der Achse)?
- Welche Winkelbeschleunigung erfährt das Rad? Wie gross ist der Betrag der Beschleunigung am vordersten Punkt des Rades (auf dem Umfang auf Höhe der Achse)?
- Skizzieren Sie das Bugrad mit allen einwirkenden Kräften, führen Sie ein geeignetes Koordinatensystem ein und formulieren Sie die drei Bilanzgleichungen (Grundgesetze).
- Wie gross sind Haftreibungs- und Normalkraft sowie die Horizontalkomponente der Kraft des Flugzeuges auf die Achse des Rades?
Aufgabe 3
Der Wärmespeicher einer grossen solarthermischen Anlage enthält geschmolzenes Salz von 527°C. Wenn man dem Speicher während zehn Minute Wärmeenergie mit einer thermischen Leistung (zugeordneter Energiestrom) von 10 MW entnimmt, sinkt die Temperatur des Speichers um 1°C.
- Um wie viel nehmen die Enthalpie und die Entropie dieses Speichers ab, wenn man ihn von 527°C auf 447°C abkühlt?
- Die dem Speicher unter a) entnommene Wärme dient dem Betrieb einer Wärmekraftmaschine, die reversibel zwischen 427°C und 27°C arbeitet. Wie viel nutzbare Energie (Arbeit oder Prozessenergie) gibt die Wärmekraftmaschine ab?
- Wie viel Entropie wird bei b) zwischen Speicher und Umgebung produziert, wenn letztere 7°C warm ist?
- Wie viel nutzbare Energie (Arbeit oder Prozessenergie) könnte man maximal gewinnen (der Speicher wird von 527°C auf 447°C abgekühlt und die Umgebungstemperatur beträgt 7°C)?
Aufgabe 4
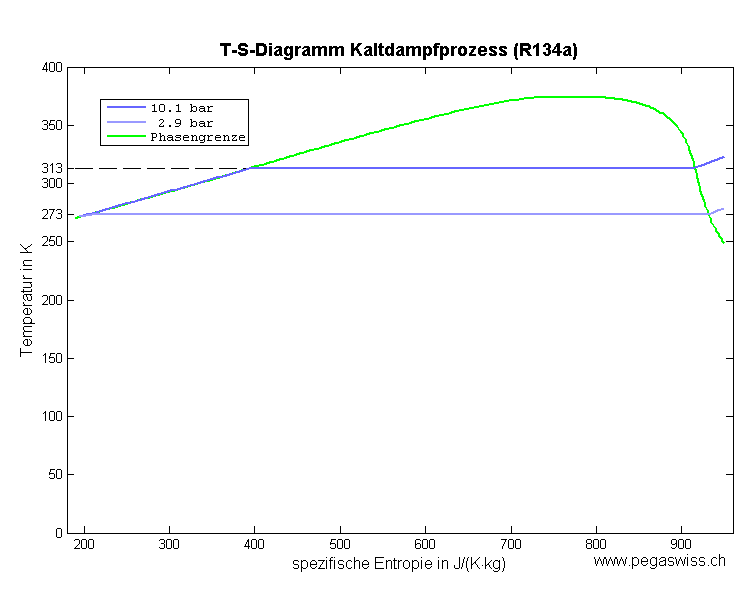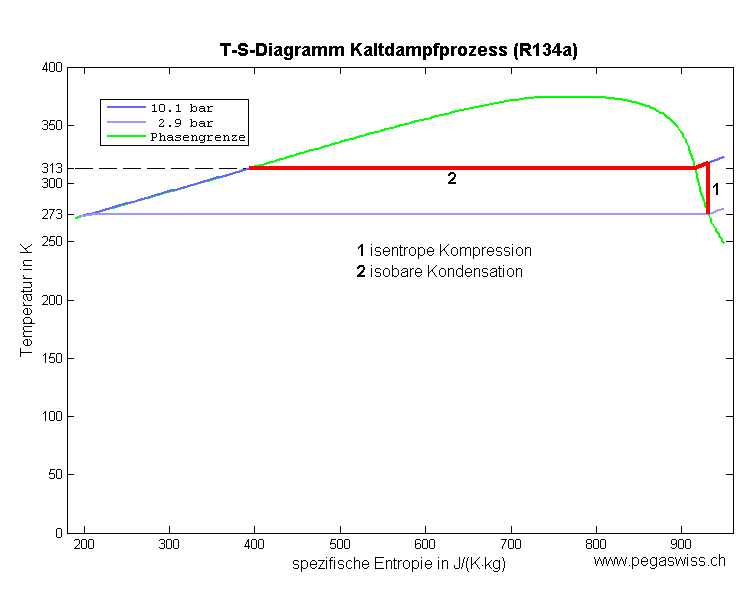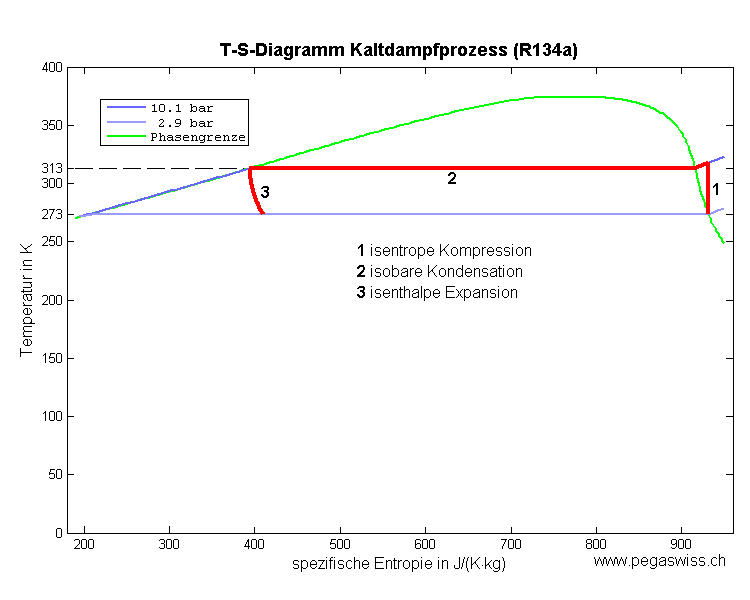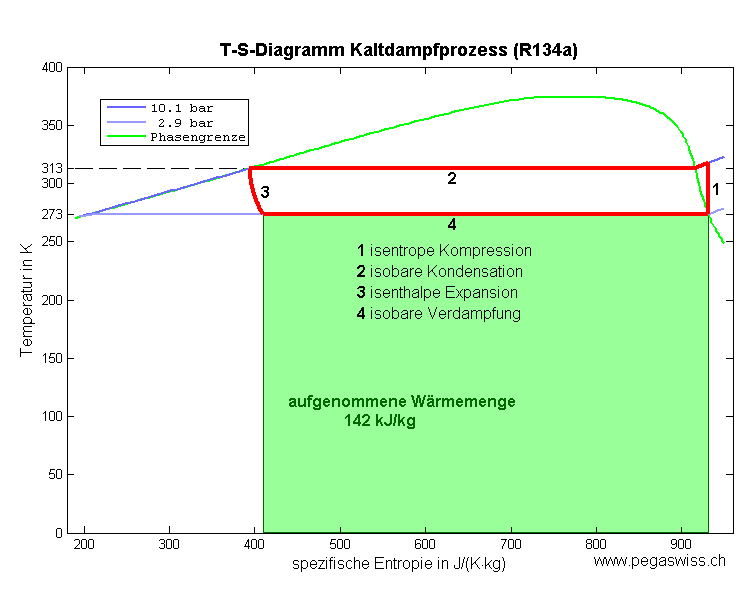
Das Diagramm zeigt den idealisierten Prozess der Wärmepumpe eines Kühlschrankes. Die Entropie ist spezifische d.h. pro Kilogramm angegeben.
- Wie viel Entropie und wie viel Wärmeenergie nimmt ein Kilogramm Kühlmittel beim Verdampfen auf (Prozess 4)?
- Wie gross ist der Unterschied zwischen abgegebener (Prozess 2) und aufgenommener Wärmeenergie (Prozess 4)?
- Für die isentrope Kompression von 2.9 bar auf 10.1 bar nehmen wir ersatzweise 10 mol ideales Gas mit einem Isentropenexponent von 1.13. Wie hoch würde die Temperatur des idealen Gases dabei steigen?
- Wie gross wäre die Kompressionsarbeit für dieses Ersatzgas unter den gegebenen Bedingungen?
Aufgabe 5
Zwei Schwungräder (Rad 1: Massenträgheitsmoment 80 kgm2, Rad 2: Massenträgheitsmoment 20 kgm2), die über eine ideale Feder miteinander verbunden sind, können durch gegenseitige Auslenkung in eine Drehschwingung versetzt werden. Die Schwingungsdauer beträgt 1.5 Sekunden.
- Wie gross ist die Winkelrichtgrösse (Drehfederkonstante) dieser Feder?
- Die Feder wird vor dem Loslassen der beiden Schwungräder um eine Viertelumdrehung verdreht. In welchem Verhältnis wird die Federenergie auf die beiden Schwungräder verteilt? Mit welcher maximalen Winkelge-schwindigkeit rotiert das grössere Schwungrad?
- Skizzieren Sie das Systemdiagramm (Flowchart) für dieses System und schreiben Sie die zugehörigen Gleichungen ins Systemdiagramm hinein (nur formal).
- Das System wird nun um eine Wirbelstrombremse ergänzt, welche das grössere Schwungrad relativ zur Erde abbremst. Ergänzen Sie das Systemdiagramm um dieses Element. Ergänzen Sie zudem das Flowchart um zwei weitere Teile, welche die Energie der Feder und die in der Wirbelstrombremse dissipierte Energie berechnet.