Lösung zu Aviatik 2016/1
Aufgabe 1
Aufgabe 2
- Unmittelbar nach dem Einschalten fliesst ein Strom der Stärke 9.09 mA. Multiplieziert mit dem Widerstand von 2500 Ω ergibt eine Spannung von 22.7 V. Zu Berechnung der Leistung mulipliziert man Strom und Spannung, was 207 mW ergibt.
- Die elektrische Ladung des Kondensators entspricht der durch den Widerstand 3 geflossenen Ladung. Demnach muss man die Fläche unter der zugehörigen Stromstärke-Zeit-Kurve bilden, was 1.12 mC entspricht.
- Zum Zeitpunkt eine Sekunde ist die Kondensatorladung praktisch maximal. Folglich fliesst der Strom nur noch durch die Widerstände 1 und 2. Diese beiden Widerstände bilden dann einen Spannungsteiler, d.h. sie teilen die angelegte Spannung von 50 V im Verhältnis ihrer Grösse. Weil nur noch ein Strom der Stärke 5 mA durch die beiden Widerstände fliesst, ist der Gesamtwidestand 10'000 Ω. Da der erste Widestand 2500 Ω beträgt, muss der zweite einen Wert von 7500 Ω haben. Die zugehörige Leistung ist dann gleich Widerstand mal Stromstärke im Quadrat, also gleich 186 mW.
- Die Kapazität ist gleich Ladung durch Spannung. Die Ladung ist in 2. berechnet worden, die Spannung von 37.5 V ergibt sich aus dem Spannungsteiler. In Simulationsprogramm (Dymola) ist für diese Kapazität 30 μ eingesetzt worden.
Aufgabe 3
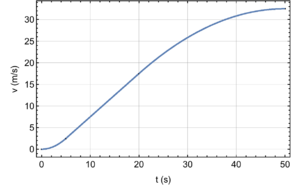
- Die Geschwindigkeit entspricht der Fläche unter der Beschleunigungs-Zeit-Kurve, was hier bis zum Zeitpunkt 50s 32.5 m/s ergibt.
- Das Geschwindigkeits-Zeit-Diagramm besteht aus einem Parabelstück, einer Geraden und einem zweiten Parabelstück. Die Übergänge müssen glatt sein, weil die Ableitung nach der Zeit (Beschleunigung) stetig ist. Die Fläche unter dieser Kurve entspricht der Strecke (ein paar Stützpunkte berechnen und Fläche bilden). Mathematisch erhält man mittels Integralrechnung den Wert 979 m.
- Der von den Antriebsräder in den Zug gepumpte Impulsstrom bleibt zum Teil im Zug und bewirkt die Beschleunigung, der Rest (gemäss gegebener Formel 5000 N) geht an die Umgebung weg oder mathematisch ausgedrückt [math]F_H = ma +F_W[/math] = 125 kN (120 kN für die Beschleunigung, 5 kN für den Widerstand nach Formel).
- Die Leistung des Antriebssystems ist gleich Impulsstromstärke mal Pumphöhe, als gleich 2.19 MW.
Aufgabe 4
- Man kann diesen Vorgang in zwei Phasen zerlegen: in der ersten Phase findet ein inelastischer Stoss zwischen Hammer und Nagel statt, in der zweiten wird das System Hammer-Nagel gleichförmig abgebremst. Der inelastische Stoss führt zu einer gemeinsamen Geschwindigkeit von 9.93 m/s und einer dissipierten Energie von 0.148 J, was verglichen mit der kinetischen Energie des Hammers von 20 J wenig ist. Deshalb steht in der Aufgabenstellung, dass dieser Energie"verlust" vernachlässigt werden kann, was die Lösung wesentlich vereinfacht: die kinetische Energie des Hammers ist gleich der Arbeit der Kraft vom Nagel auf die Wand. Somit erhält man für diese Kraft [math]F_W = \frac{mv^2}{2s}[/math] = 1000 N.
- Das Flüssigkeitsbild zeigt zwei Töpfe und zwei Impulsströme, einen vom Hammer auf den Nagel und einen vom Nagel gegen die Umgebung. Diese Aufgabe dient nur der Vorbereitung für die Lösung der Modellierungsaufgabe (Video)
Aufgabe 5
- Auf das Flugzeug wirken in der Ebene normal zur Geschwindigkeit nur zwei Kräfte, die Gewichtskraft und die Auftriebskraft (unbedingt Kraftskizze zeichnen)
- Für die Beschleunigung bei Kreisbewegung gilt: [math]a_n = \frac{v^2}{R}[/math] = 4.5 m/s2
- Die Flügelachse sollte normal zum Auftrieb stehen, womit der Tangens des Winkel gegen die Horizontale gleich dem Verhältnis der Vertikal- zur Horizontalkomponente der Auftriebskraft ist. Diese beiden Komponenten sind aber gleich der Gewichtskraft (Gleichgewicht vertikal) zu reslutierenden Kraft (Grundgesetz horizontal): [math]\alpha = \arctan\left(\frac{F_{Res}}{F_G}\right)=\arctan\left(\frac{a}{g}\right)[/math] = 24.6°
- Der Betrag der Auftriebskraft enspricht der vektoriellen Summe aus Gewichtskraft und resultierenden Kraft: [math]F_A = \sqrt{F_G^2+F_{Res}^2}=m\sqrt{g^2+a^2}[/math] = 1.295 MN
- Die lokale Gravitationsfeldstärke ist gleich der vektoriellen Summe aus statischen Gravitationsfeldstärke und Trägheitsfeldstärke. Weil die beiden Feldstärken normal zueinander stehen, kann man die lokale Feldstärke mit dem Satz von Pythagoras berechnen [math]g'=\sqrt{g^2+a_n^2}[/math] = 10.79 N/kg. Die Anzeige der Wage ist deshalb gleich 75 kg * 10.79 / 9.81 = 82.5 kg
- Die Schubkraft ist gleich der Änderung des konvektiven Impulsstromes. Folglich gilt [math]I_m = \frac{F_S}{v_2-v_1}[/math] = 233 kg/s
- Das Verhältnis der Leistung der Schubkraft am Flugzeug zu Leistung am Luftstrom nennt man äusseren Wirkungsgrad des Triebwerkes.
- [math]P=\frac{v_2^2-v_1^2}{2}I_m=\frac{v_2+v_1}{2}F_S[/math] = 7.88 MW
- [math]P=v_1F_S[/math] = 5.25 MW