Lösung zu Doppelzylindersatellit
Version vom 10. Mai 2010, 17:55 Uhr von Thomas Rüegg (Diskussion | Beiträge)
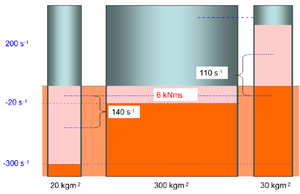
- Der erste Motor pumpt 6000 Nms Drehimpuls in den ersten Zylinder hinein. Diesen Drehimpuls entnimmt er dem Käfig (Rest des Satelliten ohne die Zylinder). Der zweite Zylinder macht zwar eine Kreisbahn, rotiert aber nicht und hat deshalb auch keinen Eigendrehimpuls gespeichert. Weil der Käfig zehn Mal langsamer in Gegenrichtung dreht, muss das zugehörige Massenträgheitsmoment zehn Mal grösser sein. Der zweite Motor fördert später Drehimpuls aus dem zweiten Zylinder in den Käfig hinein, sodass der Käfig-Drehimpuls wieder 0 wird. Dafür muss er gleich viel Drehimpuls in den Käfig hineinpumpen, wie der erste Motor herausgepumpt hat, also ebenfalls 6000 Nms.
- Der erste Motor hebt die 6000 Nms Drehimpuls im Mittel um eine Winkelgeschwindigkeitsdifferenz von (200 rad/s - (- 20 rad/s)) / 2 = 110 rad/s hinauf. Dazu muss er mindestens 110 rad/s * 6000 Nms = 660 kJ Energie aufwenden.
- Der zweite Motor fördert ebenfalls 6000 Nms Drehimpuls. Weil die mittlere Pumphöhe diesmal 140 s-1 beträgt, erhöht sich die aufzuwendende Energie auf 840 kJ. In der ersten Phase des zweiten Prozesses fliesst der Drehimpuls hinunter. In dieser Phase muss der Motor als Generator arbeiten, damit er insgesamt nur 840 kJ Energie frei setzen muss.
- Die beiden Zylinder speichern neben dem Eigendrehimpuls auch noch Bahndrehimpuls [math]L_B = mr^2 \omega[/math]. Weil die beiden Zylinderachsen gemeinsam mit dem Rest des Satelliten rotieren, tragen sie einen Beitrag von je [math]mr^2[/math] = 100 kgm2 zum Massenträgheitsmoment bei. Der Käfig besitzt folglich ein Massenträgheitsmoment von 100 kgm2.