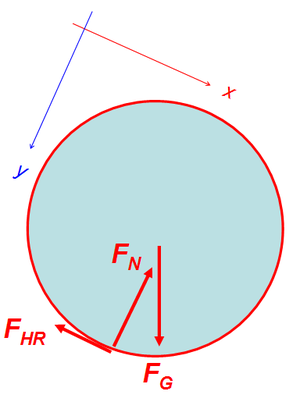
Resultate zu Rollkörper auf schiefer Ebene
1. siehe Bild rechts
2.
- [math]F_G\sin\beta-F_{HR}=\dot p_x=m\dot v_x[/math]
- [math]F_G\cos\beta-F_N=\dot p_y=0[/math]
- [math]F_{HR}\cdot r=\dot L_z=J_z \dot \omega_z[/math]
3.
- [math]\dot v = \frac {g}{k} \sin \beta[/math] mit [math]k = 1 + \frac {J}{mr^2}[/math]
4. Der Weg über die Energiebilanz ist schneller, liefert aber keine Informationen zu den Zwangskräften (Normalkraft und Haftreibungskraft)
- [math]\dot W_G+\dot W_{kin}+\dot W_{rot}=0, \quad W_G = m g h, \quad W_{kin} = \frac {m} {2} v^2, \quad W_{rot} = \frac {J}{2} \omega ^2[/math]
- [math]mg\dot h+mv\dot v+J\omega\dot\omega=0[/math]
Die Geschwindigkeit hängt mit der Änderungsrate der Höhe zusammen: [math] v = - \dot h \cdot sin\beta [/math]. Mit Hilfe der Rollbedingung eliminiert man ω und seine Änderungsrate und erhält
- [math]-mg\sin\beta v + mv\dot v+ J \frac{v\dot v}{r^2} = 0 [/math]
und daraus dann die gleiche Formel wie oben.
5. Die Kugel wird umso stärker beschleunigt, je kleiner der Faktor k ist, d.h. je weniger er von eins abweicht und je kleiner das Verhältnis des Massenträgheitsmoments zu Masse mal Quadrat des Abrollradius r ist. Mit dem Massenträgheitsmoment der Kugel J = 2/5 m R2 und Kugelradius R wird
- [math] k = 1+\frac{2 R^2}{5 r^2}[/math]
Die Kugel ist somit um so schneller, je weniger sich Abroll- und Kugelradius unterscheiden oder je kleiner die vom U-Profil gebildete "Spurweite" ist. Diese ist im Grenzfall 0 und beide Radien sind gleich.