Botafumeiro

Der Name Botafumeiro für das grosse Weihrauchfass der Kathedrale von Santiago de Compostela ist galicisch. Er setzt sich aus den Wörtern "bota" (ausstossen) und "fume" (Rauch) zusammen. Der Botafumeiro wird in der Basilika Santiagos von acht Tiraboleiros durch periodisches Ziehen an einem Seil, das über eine Umlenkrolle zum aufgehängten Weihrauchfass führt, in eine Pendelbewegung versetzt. Das spektakuläre Schauspiel, bei dem das etwa 54 kg schwere, rauchende Gefäss mit bis zu 65 km/h von der Puerta de las Platerias bis zur Puerta de Azabacheria rauscht, diente früher auch dazu, einen angenehmen Duft in der von Pilgern überfüllten Kirche zu verbreiten.

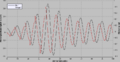
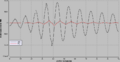
parametererregte Schwingung

In einem einfachen Modell geht man davon aus, dass das Seil im tiefsten Punkt der Bahn verkürzt und im Umkehrpunkt wieder verlängert wird. Das Seil ändert seine Länge demnach in beliebig kurzer Zeit. Zudem gehen die Leistungs- und Kraftgrenze der Tiraboleiros nicht ins Modell ein. Die Länge des Seils kann aus der Periode bei kleiner Auslenkung abgeschätzt werden

[math]T=2\pi\sqrt{\frac{L}{g}}[/math] und somit [math]L=\frac{gT^2}{4\pi^2}[/math]

Aus dem gemessenen Wert von 9 s (youtube) ergibt sich so eine Pendellänge von 20 m. Weil die Quellen von bis zu 30 m sprechen, sind im Modell 25 m eingesetzt worden. Das Seil wird von den Tiraboleiros am tiefsten Punkt der Bahn um fünf Meter verkürzt.

Das System wird als Rotator modelliert, wobei das Massenträgheitsmoment nur die Kapazität für den Bahndrehimpuls beschreibt (Masse des Gefässes mal Quadrat des Abstandes zum Drehachse). Der Gravitationskraft und dem Luftwiderstand wird je ein Drehmoment bezüglich der Drehachse zugeschrieben.

• 

  Systemdiagramm mit Gleichungen

• 

  Winkel und Winkelgeschwindigkeit

• 

  Gravitation und Luftwiderstand

Energie

Durch das Hochziehen des Botafumeiro wird dessen potentielle Energie erhöht. Gleichzeitig wird das Massenträgheitsmoment verkleinert. Dadurch erhöht sich wie bei der Pirouette die Winkelgeschwindigkeit, womit auch die Rotationsenergie zunimmt.

Die Änderung der potentiellen Energie wird teilweise rückgängig gemacht, sobald das Seil in den Umkehrpunkten wieder verlängert wird. Die Nettoänderung der potentiellen Energie pro Halbperiode ist gleich

[math]\Delta W_G=mg\Delta l(1-sin\varphi)[/math]

Die am tiefsten Punkt der Bahn erzwungene Änderung der Rotationsenergie wird in den Umkehrpunkten nicht korrigiert, weil dort die Winkelgeschwindigkeit und der Drehimpuls gleich Null sind. Die Änderung der Rotationsenergie ist gleich Drehimpuls mal Änderung der Winkelgeschwindigkeit (im Flüssigkeitsbild gleich Inhalt mal Änderung der Füllhöhe)

[math]\Delta W_{rot}=L\frac{\Delta\omega}{2}=\frac {L^2}{2}\left(\frac{1}{m(l_0-\Delta l)^2}-\frac{1}{ml_0^2}\right)[/math]

Mit L wird hier der Drehimpuls im tiefsten Punkt der Bahn bezeichnet. Zudem wird wie im systemdynamischen Modell angenommen, dass die Verkürzung des Seils im tiefsten Punkt der Bahn und die Verkürzung in den beiden Umkehrpunkten beliebig schnell erfolgt.

Links

• Modellierung des Borafumeiro] auf Youtube