Biegung: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) |
||
| (6 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Biegung tritt auf, wenn ein Körper von seitwärts |
Biegung tritt auf, wenn ein Körper von seitwärts fliessendem Drehimpuls durchströmt wird. Die Stärke dieses Drehimpulsstromes bezüglich einer ausgewählten Querschnittfläche nennt man Biegemoment. In der Regel untersucht man die Biegung prismatischer Körper (Balken, Vierkantrohr, U-, T- oder H-Balken). Hier wird angenommen, dass die ''x''-Achse in Richtung des Balkens zeigt und dass ''y''-Drehimpuls durch den Balken transportiert wird. |
||
==Drehimpulstransport== |
==Drehimpulstransport== |
||
[[Bild:DrehimpulsstromBiegung.png|thumb|Drehimpulsstrom und Impulsstrom bei Biegung]] |
[[Bild:DrehimpulsstromBiegung.png|thumb|Drehimpulsstrom und Impulsstrom bei Biegung]] |
||
Der [[Drehimpulsstrom]] kann nicht direkt gemessen werden. In ruhenden |
Der [[Drehimpulsstrom]] kann nicht direkt gemessen werden. In ruhenden Systemen ([[Statik]]) wird der Drehimpulsstrom aber immer durch [[Impulsstrom|Impulsströme]] berandet. Die Stärke dieser Impulsströme kann mit Hilfe der Verformung des durchflossene Material gemessen werden ([[Federwaage]], [[Kraftmessdose]]). Damit Drehimpuls seitwärts zu seiner Bezugsrichtung fliessen kann, muss der Transport beidseits durch Impulsströme begrenzt sein. Wird zum Beispiel ''y''-Drehimpuls in die positive ''x''-Richtung durch einen Balken transportiert, fliesst auf der einen Seite ''x''-Impuls in Richtung der ''x''-Achse (Druck) und auf der andern Seite gegen die ''x''-Achse (Zug). Das Bild zeigt wie der ''x''-Impuls- (rot) und der ''y''-Drehimpuls (blau) durch den in der Mitte nach oben gebogenen Balken fliessen. |
||
Zwischen der Drehimpulsstromdichte ''j<sub>Lyx</sub>'' und der Impulsstromdichte ''j<sub>pxx</sub>'' besteht eine spezielle Gradientenbeziehung |
Zwischen der Drehimpulsstromdichte ''j<sub>Lyx</sub>'' und der Impulsstromdichte ''j<sub>pxx</sub>'' besteht eine spezielle Gradientenbeziehung |
||
| Zeile 15: | Zeile 15: | ||
Drehimpuls kann von der Seite her über eine verdrehte Welle in den Balken eingeleitet werden. Daneben bilden sich [[Drehimpulsquelle|Drehimpulsquellen]], sobald Impuls seitwärts zu seiner Bezugsrichtung transportiert wird. |
Drehimpuls kann von der Seite her über eine verdrehte Welle in den Balken eingeleitet werden. Daneben bilden sich [[Drehimpulsquelle|Drehimpulsquellen]], sobald Impuls seitwärts zu seiner Bezugsrichtung transportiert wird. |
||
Ein Bleistift lässt sich biegen, indem man an beiden Enden mit je zwei versetzt angreifenden Fingern gegendrückt. Im Bereich der Hände fliesst dann der ''z''-Impuls (grün) entweder in positive (rechts) oder |
Ein Bleistift lässt sich biegen, indem man an beiden Enden mit je zwei versetzt angreifenden Fingern gegendrückt. Im Bereich der Hände fliesst dann der ''z''-Impuls (grün) entweder in positive (rechts) oder negative (links) ''x''-Richtung. Längs diesen beiden Stromabschnitten bilden sich Quellen (rechts) und Senken (links) des ''y''-Drehimpulses aus, wodurch ein von den Quellen nach links zu den Senken fliessender Drehimpulsstrom induziert wird. Dieser Drehimpulsstrom wird dann seinerseits wieder von sekundären Impulsströmen (rot) begleitet. Die Skizze zeigt die beiden primären Impulsströme (grün) sowie den sekundären Impulsstromkreis (rot). Diese Impulsstrombilder sind mit dem [[FE]]-Programm ''Comsol'' berechnet worden. Der Drehimpulsstrom ist hier nicht skizziert, weil er keinen direkten Einfluss auf das Materialverhalten nimmt und mit der FE-Methode auch nicht gerechnet werden kann. |
||
==Verhalten des Bauteils== |
==Verhalten des Bauteils== |
||
Geht man davon aus, dass sich das Material im Bauteil linear-elastisch verhält und vernachlässigt man die kleinen Änderungen der Geometrie des Bauteils, kann ein Zusammenhang zwischen der Stärke des durchfliessenden Drehimpulsstromes und der Veränderung des Neigungswinkels der Querschnittflächen des belasteten Bauteils gefunden werden |
|||
<math>I_{Ly} = E I_y \varphi_{y,x}</math> |
|||
Wird ''y''-Drehimpuls mit der Stromstärke ''I<sub>Ly</sub>'' in Richtung der ''x''-Achse durch ein Bauteil transportiert, werden die einzelnen Querschnittflächen des Bauteils im negativen Drehsinn gegen die ''y''-Achse verdreht: der Verdrehungsgradient ist proportional zur Stärke des durchfliessenden Drehimpulsstroms. Die Verdrehung ist umso kleiner, je grösser der [[Elastitzitätsmodul|''E-''Modul]] des Materials und je grösser das Flächenträgheitsmoment des Querschnitts ist. |
|||
==Biegelinie== |
==Biegelinie== |
||
==Links== |
|||
*[http://www.youtube.com/watch?v=mVWuVVGE2ss Biegung] auf Youtube |
|||
[[Kategorie:Rot]] |
[[Kategorie:Rot]] |
||
Aktuelle Version vom 7. März 2011, 10:26 Uhr
Biegung tritt auf, wenn ein Körper von seitwärts fliessendem Drehimpuls durchströmt wird. Die Stärke dieses Drehimpulsstromes bezüglich einer ausgewählten Querschnittfläche nennt man Biegemoment. In der Regel untersucht man die Biegung prismatischer Körper (Balken, Vierkantrohr, U-, T- oder H-Balken). Hier wird angenommen, dass die x-Achse in Richtung des Balkens zeigt und dass y-Drehimpuls durch den Balken transportiert wird.
Drehimpulstransport
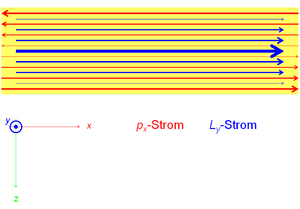
Der Drehimpulsstrom kann nicht direkt gemessen werden. In ruhenden Systemen (Statik) wird der Drehimpulsstrom aber immer durch Impulsströme berandet. Die Stärke dieser Impulsströme kann mit Hilfe der Verformung des durchflossene Material gemessen werden (Federwaage, Kraftmessdose). Damit Drehimpuls seitwärts zu seiner Bezugsrichtung fliessen kann, muss der Transport beidseits durch Impulsströme begrenzt sein. Wird zum Beispiel y-Drehimpuls in die positive x-Richtung durch einen Balken transportiert, fliesst auf der einen Seite x-Impuls in Richtung der x-Achse (Druck) und auf der andern Seite gegen die x-Achse (Zug). Das Bild zeigt wie der x-Impuls- (rot) und der y-Drehimpuls (blau) durch den in der Mitte nach oben gebogenen Balken fliessen.
Zwischen der Drehimpulsstromdichte jLyx und der Impulsstromdichte jpxx besteht eine spezielle Gradientenbeziehung
[math]j_{Lyx,z} = -j_{pxx}[/math]
Die Symbolik ,z steht für die partielle Ableitung nach der z-Koordinate.
Drehimpulseinleitung

Drehimpuls kann von der Seite her über eine verdrehte Welle in den Balken eingeleitet werden. Daneben bilden sich Drehimpulsquellen, sobald Impuls seitwärts zu seiner Bezugsrichtung transportiert wird.
Ein Bleistift lässt sich biegen, indem man an beiden Enden mit je zwei versetzt angreifenden Fingern gegendrückt. Im Bereich der Hände fliesst dann der z-Impuls (grün) entweder in positive (rechts) oder negative (links) x-Richtung. Längs diesen beiden Stromabschnitten bilden sich Quellen (rechts) und Senken (links) des y-Drehimpulses aus, wodurch ein von den Quellen nach links zu den Senken fliessender Drehimpulsstrom induziert wird. Dieser Drehimpulsstrom wird dann seinerseits wieder von sekundären Impulsströmen (rot) begleitet. Die Skizze zeigt die beiden primären Impulsströme (grün) sowie den sekundären Impulsstromkreis (rot). Diese Impulsstrombilder sind mit dem FE-Programm Comsol berechnet worden. Der Drehimpulsstrom ist hier nicht skizziert, weil er keinen direkten Einfluss auf das Materialverhalten nimmt und mit der FE-Methode auch nicht gerechnet werden kann.
Verhalten des Bauteils
Geht man davon aus, dass sich das Material im Bauteil linear-elastisch verhält und vernachlässigt man die kleinen Änderungen der Geometrie des Bauteils, kann ein Zusammenhang zwischen der Stärke des durchfliessenden Drehimpulsstromes und der Veränderung des Neigungswinkels der Querschnittflächen des belasteten Bauteils gefunden werden
[math]I_{Ly} = E I_y \varphi_{y,x}[/math]
Wird y-Drehimpuls mit der Stromstärke ILy in Richtung der x-Achse durch ein Bauteil transportiert, werden die einzelnen Querschnittflächen des Bauteils im negativen Drehsinn gegen die y-Achse verdreht: der Verdrehungsgradient ist proportional zur Stärke des durchfliessenden Drehimpulsstroms. Die Verdrehung ist umso kleiner, je grösser der E-Modul des Materials und je grösser das Flächenträgheitsmoment des Querschnitts ist.
Biegelinie
Links
- Biegung auf Youtube