Drehimpulsquelle
Bauteile wie Balken, Wellen oder Stäbe, können Drehimpuls transportieren. Die stromdurchflossenen Bauteile werden gebogen, wenn eine Drehimpuls-Komponente quer zu seiner Bezugsrichtung transportiert wird. Strömt der Drehimpuls in seine eigene Bezugsrichtung durch das Bauteil, tritt Torsion auf.
Drehimpuls kann über die Oberfläche eines Bauteils ausgetauscht werden. Der Drehimpulsstrom kann aber auch von einer Quelle gespiesen oder von einer Senke aufgezehrt werden. Eine Drehimpulssenke kann auch als Quelle mit negativer Stärke gesehen werden.
eine Komponente
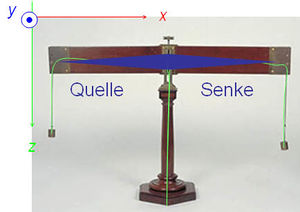
Eine Drehimpulsquelle tritt immer dann auf, wenn Impuls quer zu seiner Bezugsrichtung strömt. Fliesst z.B. ein Impulsstrom der z-Komponente in x-Richtung durch einen Balken, bilden sich längs des Transportweges Quellen des y-Drehimpulses aus. Die Skizze zeigt den z-Impulsstrom (grün) und den induzierten y-Drehimpulsstrom (blau) bei einem zweiarmigen Hebel. In den vertikal ausgerichteten Fäden herrscht Zug, weil dort der z-Impuls gegen seine Bezugsrichtung fliesst. Der Ständer wird durch den in seine Bezugsrichtung strömenden z-Impuls auf Druck belastet. In den beiden Armen des Hebels erzeugt der querfliessende z-Impulsstrom eine Quelle (links) bzw. eine Senke (rechts) bezüglich der y-Komponente des Drehimpulses. Der Hebel ist im Gleichgewicht, sobald sich die Stärken der Quellen und Senken aufheben, falls die resultierende Quellenstärke gleich null ist. Der durch die Quelle zuströmende Drehimpuls fliesst nach rechts zu den Senken, um dort aus dem System Hebel zu verschwinden. Der blaue Doppelpfeil markiert den von den Quellen zu den senken fliessenden y-Drehimpulsstrom. Die Stärke dieses Drehimpulsstromes heisst auch Biegemoment.
Mathematisch wird der Zusammenhang zwischen der Quellenstärke und den querfliessenden Impulsströmen durch das Hebelgesetz beschrieben. Die Stärke der y-Drehimpulsquelle ist proportional zur Stärke des z-Impulsstropmes und proportional zur Distand (Δ x), um die der z-Drehimpuls quer zu seiner Bezugsrichtung fliesst
- [math]\Sigma_{Ly} = \Delta x I_{pz}[/math]
im Raum
Der Impuls ist ein polarer und der Drehimpls ein achsialer Vektor. Den vollständigen Zusammenhang zwischen einem Impuls- und den Drehimpulsquellen findet man durch eine symmetrische Ergänzung und zyklisches vertauschen der oben formulierten Gleichung
- [math]\begin{pmatrix} \Sigma_{Lx}\\ \Sigma_{Ly} \\ \Sigma_{Lz}\end{pmatrix} = \begin{pmatrix} \Delta z I_{py} - \Delta y I_{pz}\\ \Delta x I_{pz} - \Delta z I_{px} \\ \Delta y I_{px} - \Delta x I_{py}\end{pmatrix}[/math]
wobei Δr (Δx, Δy, Δz) die Strecke darstellt, um die der Impuls seitwärts fliesst.
Drehmoment
Die Stärken der Impulsströme und Impulsquellen bezüglich eines Körpers nennt man Kräfte. Analog dazu nennt man die Stärken der Drehimpulsströme und Drehimpulsquellen Drehmomente. Einen reines Drehmoment kann mit Hilfe eines Kräftepaares (Stärke des Impulsstromes bei der Ein- und Austrittsstelle) definiert werden
- [math]\vec M = \vec s \times \vec F[/math]
Der Vektor s zeigt von einer Kraft des Paares zur andern und entspricht den Strecken Δ x, Δ y, Δ z in der Formulierung der Stärke der Drehimpulsquelle.