Lösung zu Wurf nach oben: Unterschied zwischen den Versionen

Inhalt hinzugefügt Inhalt gelöscht

Inline

Aktuelle Version vom 11. Dezember 2012, 16:27 Uhr

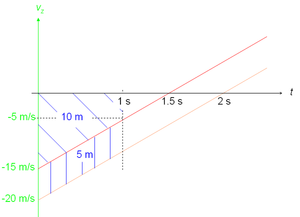
Die Beschleunigung aller im Vakuum geworfenen Körper ist gleich g = 10 m/s², falls die Bezugsrichtung nach unten zeigt. Der Rest ist einfache Kinematik.

Feder und Kugel starten gleichzeitig, aber mit verschiedenen Startgeschwindigkeiten. Ihre Geschwindigkeiten nehmen mit der gleichen Rate zu, nämlich mit a = g = 10 m/s². Deshalb bleibt die Schnelligkeit der Feder immer 20 m/s - 15 m/s = 5 m/s grösser als die der Bleikugel, siehe auch v-t-Diagramm. Da der Startabstand 5 m beträgt, holt die Feder die Kugel nach 5 m / 5 m/s = 1 s ein (benötigte Zeit = Abstand / Relativgeschwindigkeit, Abstand = Fläche zwischen den v-Kurven).
Aus dem v-t-Diagramm liest man folgendes: Die Bleikugel bewegt sich dann noch mit -5 m/s (nach oben) und die Schnelligkeit (Betrag der Geschwindigkeit) der Feder ist von 20 m/s auf 10 m/s gesunken (die Geschwindigkeit ist von -20 m/s auf -10 m/s gestiegen).
Die Bleikugel ist in dieser Sekunde um 1 s * (15 m/s + 5 m/s) / 2 = 10 m aufgestiegen (Trapezfläche unter der Kurve im Geschwindigkeits-Zeit-Diagramm).

Aufgabe

@@ Zeile 1: / Zeile 1: @@
 [[Bild:Wurf_oben.png|thumb|v-t-Diagramm der geworfenen Körper]]
 Die Beschleunigung aller im Vakuum geworfenen Körper ist gleich g = 10 m/s<sup>2</sup>, falls die Bezugsrichtung nach unten zeigt. Der Rest ist einfache Kinematik.
-#Feder und Kugel starten gleichzeitig, aber mir verschiedenen Startgeschwindigkeiten. Ihre Geschwindigkeiten nehmen mit der gleichen Rate zu, nämlich mit a = g = 10 m/s<sup>2</sup>. Deshalb bleibt die Geschwindigkeit der Feder immer 20 m/s - 15 m/s = 5 m/s [[Schnelligkeit|schneller]] als die der Bleikugel. Da der Startabstand 5 m beträgt, holt die Feder die Kugel nach einer Sekunde ein.
+#Feder und Kugel starten gleichzeitig, aber mit verschiedenen Startgeschwindigkeiten. Ihre Geschwindigkeiten nehmen mit der gleichen Rate zu, nämlich mit a = g = 10 m/s<sup>2</sup>. Deshalb bleibt die [[Schnelligkeit]] der Feder immer 20 m/s - 15 m/s = 5 m/s grösser als die der Bleikugel, siehe auch ''v-t-''Diagramm. Da der Startabstand 5 m beträgt, holt die Feder die Kugel nach 5 m / 5 m/s = 1 s ein (benötigte Zeit = Abstand / Relativgeschwindigkeit, Abstand = Fläche zwischen den ''v''-Kurven).
-#Die Bleikugel bewegt sich dann noch mit 5 m/s nach oben und die [[Schnelligkeit]] der Feder ist von 20 m/s auf 10 m/s gesunken (die [[Geschwindigkeit]] ist von -20 m/s auf -10 m/s gestiegen).
+#Aus dem ''v-t-''Diagramm liest man folgendes: Die Bleikugel bewegt sich dann noch mit -5 m/s (nach oben) und die [[Schnelligkeit]] (Betrag der Geschwindigkeit) der Feder ist von 20 m/s auf 10 m/s gesunken (die [[Geschwindigkeit]] ist von -20 m/s auf -10 m/s gestiegen).
-#Die Bleikugel ist in dieser Sekunde um 10 m aufgestiegen (Fläche unter der Kurve im Geschwindigkeits-Zeit-Diagramm).
+#Die Bleikugel ist in dieser Sekunde um 1 s * (15 m/s + 5 m/s) / 2 = 10 m aufgestiegen (Trapezfläche unter der Kurve im Geschwindigkeits-Zeit-Diagramm).
 '''[[Wurf nach oben|Aufgabe]]'''