Lösung zu DGL 1. Ordnung mit konstanten Koeffizienten: Unterschied zwischen den Versionen
Inhalt hinzugefügt Inhalt gelöscht
KP14 (Diskussion | Beiträge) (Erstellen der Lösung) |
KP14 (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
1. |
|||
Aufgabe 2 |
|||
<math>\dot V=V_0\cdot \frac{-1}{RC}\cdot e^{-t/RC}</math> in die DGL einsetzen liefert genau die angenommene Lösung (q.e.d.). |
|||
| ⚫ | |||
2. |
|||
| ⚫ | |||
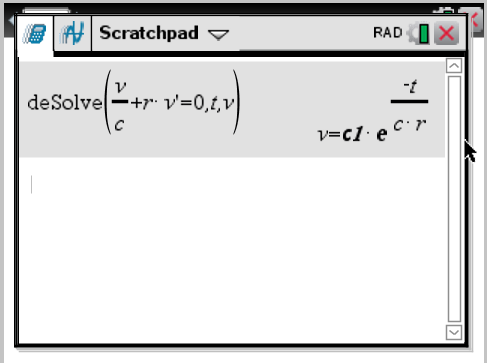
[[Datei:DGL_1_Ordnung_mit_konstanten_Koeffizienten_TI-NSpire.png|Lösung mit TI-NSpire]] |
|||
3. |
|||
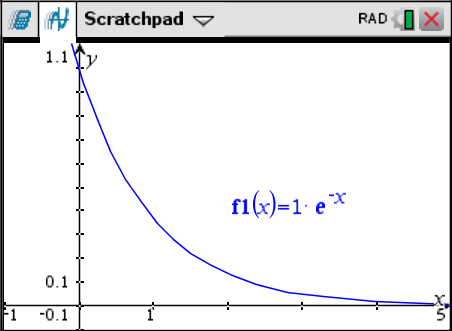
[[Datei:DGL_1_Ordnung_mit_konstanten_Koeffizienten_Verlauf.png|Spannungsverlauf]] |
|||
4. Mit <math>R=1 (Pa⋅s)/m^3</math> , <math>C=1 m^3/Pa</math> und <math>V_0=1 m^3</math> wird <math>τ=1 s</math>. Nach 1s ist das Volumen um <math>e^{-1}=0.367=36.7%</math> auf 63.2% abgefallen. |
|||
5. Die Tangente schneidet die ''t''-Achse genau bei ''τ'', also bei 1s. |
|||
Aktuelle Version vom 5. Mai 2015, 08:29 Uhr
1. [math]\dot V=V_0\cdot \frac{-1}{RC}\cdot e^{-t/RC}[/math] in die DGL einsetzen liefert genau die angenommene Lösung (q.e.d.).
2.
3.
4. Mit [math]R=1 (Pa⋅s)/m^3[/math] , [math]C=1 m^3/Pa[/math] und [math]V_0=1 m^3[/math] wird [math]τ=1 s[/math]. Nach 1s ist das Volumen um [math]e^{-1}=0.367=36.7%[/math] auf 63.2% abgefallen.
5. Die Tangente schneidet die t-Achse genau bei τ, also bei 1s.