Rohrreibungszahl: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) (Die Seite wurde neu angelegt: Steigt der Volumenstrom in einem Rohr über eine kritische Grenze, nimmt die Strömung ein turbulentes Verhalten an. Der Druckabfall über dem Rohrstück wächst dann q...) |
Admin (Diskussion | Beiträge) KKeine Bearbeitungszusammenfassung |
||
| (3 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Die Rohrreibungszahl dient in erster Linie der quantitativen Beschreibung des Rohrreibung bei turbulenter Strömung. Der Druckabfall über dem [[gerades Rohrstück|Rohrstück]] steigt bei turbulenter Strömung quadratisch zur Volumenstromstärke |
|||
:<math>\Delta p = kI_V^2</math> |
:<math>\Delta p = kI_V^2</math> |
||
Der Faktor ''k'' ist proportional zur Dichte des strömenden Mediums und zur Länge des Rohres. |
Der Faktor ''k'' ist proportional zur Dichte des strömenden Mediums und zur Länge des Rohres. Zudem nimmt er mit dem Durchmesser hoch fünf ab |
||
:<math>k=\zeta \frac {\ |
:<math>k=\zeta \frac {\varrho} {2A^2}=\lambda \frac {8 \varrho l}{\pi^2d^5}</math> |
||
[[Bild:Rohrreibungszahl.jpg|thumb|lambda von Re]]Die dimensionslose Grösse ''ζ'' (zeta) ist die [[Verlustziffer]] und die ebenfalls dimensionslose Grösse ''λ'' (lambda) heisst Rohrreibungszahl. Die Rohrreibungszahl hängt aber immer noch von der Volumenstromstärke ab. Um diese Abhängigkeit losgelöst vom konkreten Medium beschreiben zu können, gibt man die Rohrreibungszahl in Funktion der ebenfalls dimensionslosen [[Reynolds-Zahl]] Re an. De Graphik zeigt, wie die Rohrreibungszahl verschieden rauer Rohre von der Reynolds-Zahl abhängt. |
|||
Die dimensionslose Grösse ''ζ'' (Zeta) heisst '''Widerstandszahl'''. Eine Widerstandszahl kann für jede turbulent durchströmte Armatur angegeben werden. Für eine gerades Stück Rohr ist die Widerstandszahl von der Länge, dem Durchmesser und der ebenfalls dimensionslosen Rohrreibungszahl abhängig |
|||
Im [[laminare Strömung|laminaren]] Bereich steigt der Druck linear mit dem Volumenstrom |
|||
:<math>\Delta p=R_V I_V</math> |
|||
wobei für den Strömungswiderstand gilt |
|||
:<math>R_V=\frac{128\eta l}{\pi d^4}</math> |
|||
Rein algebraisch lässt sich das laminare Strömungsgesetz ins turbulente umschreiben, in der Strömungswiderstand umgeschrieben wird |
|||
:<math>\Delta p=R_V I_V=\frac{R_V}{I_V}I_V^2=\frac{64\eta}{\pi^2d^6v}=\frac{64\eta}{\varrho d v}\frac{8\varrho l}{\pi^2d^5}=\frac{64}{Re}\frac{8\varrho l}{\pi^2d^5}</math> |
|||
Im laminaren Bereich darf die Rohrreibungszahl mit <math>\lambda=\frac{64}{Re}</math> angegeben werden. Weil das [[Fluid]] die Wand benetzt und der ganze Widerstand über Scherkräfte (quer fliessende Impulsströme) aufgebaut wird, spielt die Rauigkeit des Rohres keine Rolle. |
|||
[[Kategorie:Hydro]] |
|||
Aktuelle Version vom 26. Dezember 2007, 07:45 Uhr
Die Rohrreibungszahl dient in erster Linie der quantitativen Beschreibung des Rohrreibung bei turbulenter Strömung. Der Druckabfall über dem Rohrstück steigt bei turbulenter Strömung quadratisch zur Volumenstromstärke
- [math]\Delta p = kI_V^2[/math]
Der Faktor k ist proportional zur Dichte des strömenden Mediums und zur Länge des Rohres. Zudem nimmt er mit dem Durchmesser hoch fünf ab
- [math]k=\zeta \frac {\varrho} {2A^2}=\lambda \frac {8 \varrho l}{\pi^2d^5}[/math]
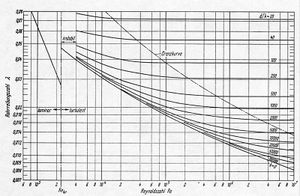
Die dimensionslose Grösse ζ (zeta) ist die Verlustziffer und die ebenfalls dimensionslose Grösse λ (lambda) heisst Rohrreibungszahl. Die Rohrreibungszahl hängt aber immer noch von der Volumenstromstärke ab. Um diese Abhängigkeit losgelöst vom konkreten Medium beschreiben zu können, gibt man die Rohrreibungszahl in Funktion der ebenfalls dimensionslosen Reynolds-Zahl Re an. De Graphik zeigt, wie die Rohrreibungszahl verschieden rauer Rohre von der Reynolds-Zahl abhängt.
Im laminaren Bereich steigt der Druck linear mit dem Volumenstrom
- [math]\Delta p=R_V I_V[/math]
wobei für den Strömungswiderstand gilt
- [math]R_V=\frac{128\eta l}{\pi d^4}[/math]
Rein algebraisch lässt sich das laminare Strömungsgesetz ins turbulente umschreiben, in der Strömungswiderstand umgeschrieben wird
- [math]\Delta p=R_V I_V=\frac{R_V}{I_V}I_V^2=\frac{64\eta}{\pi^2d^6v}=\frac{64\eta}{\varrho d v}\frac{8\varrho l}{\pi^2d^5}=\frac{64}{Re}\frac{8\varrho l}{\pi^2d^5}[/math]
Im laminaren Bereich darf die Rohrreibungszahl mit [math]\lambda=\frac{64}{Re}[/math] angegeben werden. Weil das Fluid die Wand benetzt und der ganze Widerstand über Scherkräfte (quer fliessende Impulsströme) aufgebaut wird, spielt die Rauigkeit des Rohres keine Rolle.