Strahlkontraktion: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
[[Bild:Strahlkontraktion.png|thumb|Behälter mit Bilanzgebiet]]Tritt Flüssigkeit durch ein scharfkantiges Loch ins freie, misst der Querschnitt des Freistrahls nur etwa 60% des Lochquerschnitts. Mit Hilfe einer [[Energiebilanz|Energie]]- und einer [[Impulsbilanz]] kann eine untere Grenze für diese Strahlkontraktion gefunden werden. |
[[Bild:Strahlkontraktion.png|thumb|Behälter mit Bilanzgebiet]]Tritt Flüssigkeit durch ein scharfkantiges Loch ins freie, misst der Querschnitt des Freistrahls nur etwa 60% des Lochquerschnitts. Mit Hilfe einer [[Energiebilanz|Energie]]- und einer [[Impulsbilanz]] kann eine untere Grenze für diese Strahlkontraktion gefunden werden. |
||
Aus einem unter Druck stehenden Behälter strömt eine Flüssigkeit mit der Geschwindigkeit ''v'' ins freie |
Aus einem unter Druck stehenden Behälter strömt eine Flüssigkeit mit der Geschwindigkeit ''v'' ins freie. Wählt man nun das Gebiet im Innern des Behälters so, dass das Loch ein Teil von dessen Oberfläche bildet, kann eine Impulsbilanz formuliert werden. Auf das Bilanzgebiet wirkt bis auf das Loch allseitig der Überdruck ''p'' ein. Die resutlierende Druckkraft auf das Bilanzgebiet ist gleich Druck mal Querschnitt des Lochs. Diese [[Kraft]] zeigt auf das Loch zu, weil dieses nicht in der Lage ist, die Kraft des gegenüberliegenden, gleich grossen Stücks zu kompensieren. Der konvektive [[Impulsstrom]] der austretenden Flüssigkeit kann ebenfalls als Kraft betrachtet werden, die vom Loch her auf das Bilanzgebiet einwirkt. Weil sich der Impuls dieses Gebiets nicht ändert, sind die beiden Ströme, die Druckkraft und der konvektive Impulsstrom, entgegengesetzt gleich stark, d.h. ihre Beträge sind gleich |
||
:<math>F_D=pA_{Loch}=I_p=vI_m=\varrho A_{Strahl} v^2</math> |
:<math>F_D=pA_{Loch}=I_p=vI_m=\varrho A_{Strahl} v^2</math> |
||
Aus der Energiebilanz oder der direkten Anwendung des [[Gesetz von Bernoulli|Satzes von Bernoulli]] folgt, dass die Dichte der kinetischen Energie im Strahl gleich dem |
Aus der Energiebilanz oder der direkten Anwendung des [[Gesetz von Bernoulli|Satzes von Bernoulli]] folgt, dass die Dichte der kinetischen Energie im Strahl gleich dem Überdruck im Behälter ist |
||
:<math>p=\frac{\varrho}{2}v^2</math> |
:<math>p=\frac{\varrho}{2}v^2</math> |
||
| Zeile 11: | Zeile 11: | ||
Durch Einsetzen in die Impulsbilanz erhält man |
Durch Einsetzen in die Impulsbilanz erhält man |
||
:<math>\frac{ |
:<math>\frac{A_{Loch}}{A_{Strahl}}=2</math> |
||
Der Strahl schnürt sich gemäss dieser Betrachtung |
Der Strahl schnürt sich gemäss dieser Betrachtung so stark ein, dass sein Querschnitt um 50% kleiner wird als die freie Fläche des Lochs. Zwei Effekte beeinflussen dieses Resultat |
||
#In der Umgebung des Loches kann der Impuls radial zu |
#In der Umgebung des Loches kann der Impuls seitwärts zu seiner Bezugsrichtung, also radial, zu oder weg fliessen. Dieser Austausch wird durch die grosse Viskosität und durch abgerundete Kanten begünstigt. |
||
#In der Übergangszone zum Freistrahl gleicht sich die Strömungsgeschwindigkeit im ganzen Querschnitt der Strömung unter [[Dissipation]] von Energie an. |
|||
[[Kategorie:Hydro]] |
|||
Aktuelle Version vom 8. Januar 2008, 19:18 Uhr
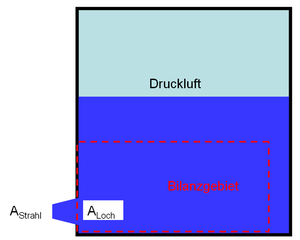
Tritt Flüssigkeit durch ein scharfkantiges Loch ins freie, misst der Querschnitt des Freistrahls nur etwa 60% des Lochquerschnitts. Mit Hilfe einer Energie- und einer Impulsbilanz kann eine untere Grenze für diese Strahlkontraktion gefunden werden.
Aus einem unter Druck stehenden Behälter strömt eine Flüssigkeit mit der Geschwindigkeit v ins freie. Wählt man nun das Gebiet im Innern des Behälters so, dass das Loch ein Teil von dessen Oberfläche bildet, kann eine Impulsbilanz formuliert werden. Auf das Bilanzgebiet wirkt bis auf das Loch allseitig der Überdruck p ein. Die resutlierende Druckkraft auf das Bilanzgebiet ist gleich Druck mal Querschnitt des Lochs. Diese Kraft zeigt auf das Loch zu, weil dieses nicht in der Lage ist, die Kraft des gegenüberliegenden, gleich grossen Stücks zu kompensieren. Der konvektive Impulsstrom der austretenden Flüssigkeit kann ebenfalls als Kraft betrachtet werden, die vom Loch her auf das Bilanzgebiet einwirkt. Weil sich der Impuls dieses Gebiets nicht ändert, sind die beiden Ströme, die Druckkraft und der konvektive Impulsstrom, entgegengesetzt gleich stark, d.h. ihre Beträge sind gleich
- [math]F_D=pA_{Loch}=I_p=vI_m=\varrho A_{Strahl} v^2[/math]
Aus der Energiebilanz oder der direkten Anwendung des Satzes von Bernoulli folgt, dass die Dichte der kinetischen Energie im Strahl gleich dem Überdruck im Behälter ist
- [math]p=\frac{\varrho}{2}v^2[/math]
Durch Einsetzen in die Impulsbilanz erhält man
- [math]\frac{A_{Loch}}{A_{Strahl}}=2[/math]
Der Strahl schnürt sich gemäss dieser Betrachtung so stark ein, dass sein Querschnitt um 50% kleiner wird als die freie Fläche des Lochs. Zwei Effekte beeinflussen dieses Resultat
- In der Umgebung des Loches kann der Impuls seitwärts zu seiner Bezugsrichtung, also radial, zu oder weg fliessen. Dieser Austausch wird durch die grosse Viskosität und durch abgerundete Kanten begünstigt.
- In der Übergangszone zum Freistrahl gleicht sich die Strömungsgeschwindigkeit im ganzen Querschnitt der Strömung unter Dissipation von Energie an.