Lösung zu Aviatik 2006/Ass: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) (Die Seite wurde neu angelegt: Jede Aufgabe wird mit 4 Punkten bewertet. == Lösung zu Aufgabe 1 == 1.) Die Stärke des Volumenstromes beträgt 0.0133 m<sup>3</sup>/s. Dies ergibt bei einem Druckun...) |
Admin (Diskussion | Beiträge) |
||
| (18 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
== Lösung zu Aufgabe 1 == |
== Lösung zu Aufgabe 1 == |
||
1.) Die Stärke des Volumenstromes beträgt 0.0133 m<sup>3</sup>/s. Dies ergibt bei einem Druckunterschied über der Pumpe von 6.5 bar |
1.) Die Stärke des Volumenstromes beträgt 0.0133 m<sup>3</sup>/s. Dies ergibt bei einem Druckunterschied über der Pumpe von 6.5 bar eine [[Prozessleistung]] von |
||
:<math>P=\Delta pI_V</math> = 6.5*10<sup>5</sup> * 0.0133 m<sup>3</sup>/s = 8.67 kW |
:<math>P=\Delta pI_V</math> = 6.5*10<sup>5</sup> * 0.0133 m<sup>3</sup>/s = 8.67 kW |
||
| Zeile 10: | Zeile 10: | ||
:<math>\Delta p=kI_V^2</math> |
:<math>\Delta p=kI_V^2</math> |
||
Aus den gegebenen Daten |
Aus den gegebenen Daten berechnet sich die Konstante für einen Leitungsabschnitt von 300 m auf ''k'' = 2.025*10<sup>9</sup> Pas<sup>2</sup>/m<sup>6</sup>. Die in diesem Abschnitt dissipierte Leistung ist folglich gleich |
||
:<math>P=\Delta pI_V=kI_V^3</math> = 2.025 kW |
:<math>P=\Delta pI_V=kI_V^3</math> = 2.025 kW |
||
3.) Die Stärke |
3.) Die Stärke eines linear anschwellenden Stromes kann wir folgt beschrieben werden |
||
:<math>I_V=at</math> mit ''a'' = 1.667*10<sup>-3</sup> m<sup>3</sup>/s<sup>2</sup> |
:<math>I_V=at</math> mit ''a'' = 1.667*10<sup>-3</sup> m<sup>3</sup>/s<sup>2</sup> |
||
| Zeile 21: | Zeile 21: | ||
:<math>W=\int Pdt=\int kI_V^3dt=\int ka^3t^3=\frac k4 a^3t^4</math> = 9.6 kJ |
:<math>W=\int Pdt=\int kI_V^3dt=\int ka^3t^3=\frac k4 a^3t^4</math> = 9.6 kJ |
||
== Lösung zu Aufgabe 2 == |
|||
1.) Zum Zeitnullpunkt fliesst der Strom durch den Widerstand 1 und durch den Kondensator (ein ungeladener Kondensator verhält sich wie ein Kurzschluss). Deshalb liegt anfänglich die volle Spannung von 6 V über dem ersten Widerstand. Über dem zweiten Widerstand ist dann die Spannung gleich Null. 40 ms später ist der Kondensator geladen und lässt keinen Strom mehr durch. Der Strom fliesst dann nacheinander durch die beiden Widerstände, welche die Spannung von 6V entsprechend ihrer Grösse aufteilen. |
|||
2.) Zum Zeitnullpunkt setzt sich nur der erste Widerstand der Spannung entgegen |
|||
:<math>R_1=\frac{U_0}{I}</math> = 6V / 0.03A = 200Ω |
|||
Im stationären Zustand fliesst bei einer Gesamtspannung von 6 V ein Strom von 20 mA durch beide Widerstände. Folglich beträgt der totale Widerstand |
|||
:<math>R_{tot}=\frac{U_0}{I}</math> = 300Ω |
|||
Weil der erste Widerstand eine Grösse von 200Ω aufweist, muss der zweite einen Wert von 100Ω haben. Die beiden Widerstände teilen dann die angelegte Spannung im Verhältnis 2:1 (4 V und 2 V). |
|||
3.) Zum Zeitnullpunkt wird am meisten Leistung diessipiert (kleinster Gesamtwiderstand bei gegebener Spannung) |
|||
:<math>P=UI=RI^2</math> = 0.18 W |
|||
4.) Die Grösse der Kapazität kann auf zwei Arten abgeschätzt werden: |
|||
*In der ersten Vorgehensweise bestimmt man die auf den Kondensator geflossene Ladung. Diese ergibt sich als Differenz zwischen der durch den Widerstand 1 und der durch den Widerstand 2 geflossene Ladung (Flächen unter der Strom-Zeit-Kurve). Dividiert man diese Ladung durch die Endspannung von 2 V, erhält man eine Kapazität von 100μF. |
|||
*Im zweiten Verfahren bestimmt man die Zeitkonstante beim Entladen des Kondensators (Tangente an einen beliebigen Punkt der Kurve und Schnittpunkt mit der Nulllinie bestimmen; die Zeitkonstante ist dann gleich dem zugehörigen Abschnitt auf der Zeitachse). Bei einem [[RC-Glied]] ist die Zeitkonstante gleich Widerstand mal Kapazität(''τ = RC''). |
|||
== Lösung zu Aufgabe 3 == |
|||
Das Geschwindigkeits-Zeit-Diagramm entspricht dem Füllhöhen-Zeit-Diagramm im [[Flüssigkeitsbild]]. |
|||
1.) Im Flüssigkeitsbild wird der elastische Stoss als vollständiges "Überschwingen" der beiden Wassersäulen dargestellt. Der schwere Wagen (auflaufender oder Hammerwagen) würde sich nach dem Stoss mit 0.6 m/s und der leichtere Ambosswagen mit 3.6 m/s vorwärts bewegen. |
|||
2.) Die Steigung der ''v-t-''Kurve entspricht der Beschleunigung (-2 m/s<sup>2</sup>). Multipliziert man diese mit der Masse, erhält man die Impulsänderungsrate (-80 kN). Diese Rate entspricht der resultierenden Kraft. Diese setzt sich hier nur aus der Reibungskraft zusammen (80 kN entgegen der Bewegungsrichtung). |
|||
3.) Die Verschiebung des Wagens entspricht der zugehörigen Fläche unter dem Geschwindigkeits-Zeit-Diagramm (2.3 m). |
|||
4.) Die dissipierte Energie entspricht in dieser Zeitspanne der Änderung der kinetischen Energie des auflaufenden Wagens (Hammerwagen). Im fraglichen Zeitabschnitt ändert der schwerere Wagen seine Geschwindigkeit von 0.93 m/s auf 1.5 m/s |
|||
:<math>W_{diss}=\Delta W_{kin}=\frac m2\left(v_{vor}^2-v_{nach}^2\right)</math> = 25.4 kJ |
|||
== Lösung zu Aufgabe 4 == |
|||
1.) Die Vertikalbeschleunigung zu Beginn des Loopings entspricht gerade der Normalbeschleunigung auf der Kreisbahn |
|||
:<math>a_n=\frac {v^2}{r}</math> = 26.1 m/s<sup>2</sup> |
|||
2.) Auf das Flugzeug wirken nur das Gravitationsfeld und die Luft ein. Aus der [[Impulsbilanz]] in vertikaler Richtung (positive Richtung nach oben) |
|||
:<math>F_L-F_G=\dot p=m\dot v=ma_n</math> |
|||
folgt deshalb |
|||
:<math>F_L=F_G+ma_n=m(g+a_n)</math> = 108 kN |
|||
3.) Am höchsten Punkt der Bahn beträgt die Radialbeschleunigung infolge kleinerer Geschwindigkeit nur noch 4.8 m/s<sup>2</sup> (nach unten). Geht man ins mitbeschleunigte System Flugzeug, misst man eine lokale Gravitationsfeldstärke von |
|||
:<math>g'=g-g_t</math> = 10 N/kg - 4.8 N/kg =5.2 N/kg (nach unten) |
|||
Weil die Beschleunigung des Flugzeuges ([[Bezugssystem]]) nach unten gerichtet ist, zeigt das Trägheitsfeld mit der Stärke ''g<sub>t</sub>'' nach oben. Relativ zum Flugzeug ist der Pilot im Gleichgewicht, also müssen die Gurten den Piloten mit |
|||
:<math>F_{Gurt}=F'_G=mg'</math> = 390 N |
|||
nach oben ziehen |
|||
4.) Diese vergleichende Zusatzaufgabe löst man am einfachsten über eine Energiebilanz zu zwei Zeitpunkten |
|||
:<math>W_{G1}+W_{kin1}=W_{G2}+W_{kin3}</math> oder <math>\Delta W_G +\Delta W_{kin}=0</math> |
|||
Wählt man den Bezugspunkt für die Höhe bei 1 und schreibt für die Höhe 2 einfach nur ''h'', erhält man |
|||
:<math>\frac m2 v_1^2=mgh+\frac m2 v_2^2</math> |
|||
Daraus folgt |
|||
:<math>h=\frac{v_1^2-v_2^2}{2g}</math> = 800 m |
|||
==Lösung zu Aufgabe 5 == |
|||
1.) Im Horizontalflug kompensieren sich Auftriebs- und Gewichtskraft (vertikal) sowie Schub- und Luftwiderstandskraft (horizontal). Folglich ist das Verhältnis von Widerstand zu Auftrieb gleich dem Verhältnis von Gewicht (2.4 MN) zu Schub (4 * 40 kN = 160 kN), also gleich 1:15. |
|||
2.) Nimmt man an, dass die Luft ungehindert in die Öffnung eines Triebwerk eindringt, ergibt sich für den Massenstrom |
|||
:<math>I_m=\varrho I_V=\varrho A v</math> = 232 kg/s |
|||
3.) Im stationären Betrieb ist die Schubkraft (leitungsartig an das Flugzeug abfliessender [[Impulsstrom]]) gleich der Impulsänderungsrate des durchfliessenden Massenstromes |
|||
:<math>F_S=(v_2-v_1)I_m</math> |
|||
Daraus folgt für die Geschwindigkeit der austretenden Gase |
|||
:<math>v_2=\frac{F_S}{I_m}+v_1</math> = 412 m/s |
|||
4.) Die im Triebwerk auf den Gasstrom aufgeladen Leistung ist gleich der Differenz der beiden (kinetischen) Energieströme |
|||
:<math>P=I_{W_{kin2}}-I_{W_{kin1}}=\left(v_2^2-v_1^2\right)\frac{I_m}{2}=\overline v F_S</math> = 13 MW |
|||
== Lösung zu Aufgabe 6 == |
|||
Diese Aufgabe ist mit dem Problem der [[Bowling]]-Kugel verwandt. |
|||
1.) Auf den rotierenden Zylinder wirken die '''Gewichtskraft''' (nach unten), die '''Normalkraft''' (nach oben) sowie die '''Gleitreibungskraft''' (nach vorn). |
|||
2.) Der Impulstopf (Grundfläche ''m'') ist anfänglich leer und füllt sich dann unter der Wirkung der Gleitreibungskraft ''F<sub>R</sub>'' bis zur Endgeschwindigkeit ''v<sub>e</sub>''. Der Drehimpulstopf (Grundfläche ''J'') ist anfänglich bis ''ω<sub>a</sub>'' gefüllt. Unter der Wirkung des Drehmoments der Gleitreibungskraft (''M=r*F<sub>R</sub>'') sinkt dessen Niveau auf ''ω<sub>e</sub>'' ab. |
|||
3.) Das Verhältnis zwischen Drehimpulsänderung und Impulsänderung ist gleich dem Verhältnis zwischen Drehmoment und Kraft (die beiden Inhaltsänderungen sind gleich gekoppelt wie die zugehörigen Ströme) |
|||
:<math>\frac{rF_r}{F_R}=\frac{\Delta L}{\Delta p}=\frac{J(\omega_a-\omega_e)}{mv_e}</math> |
|||
Nun ist die Endgeschwindigkeit über die Rollbedingung mit der Endwinkelgeschwindigkeit verknüpft. Setzt man diese Rollbedingung <math>\left(v_e=r\omega_e\right)</math> ein, erhält man eine Gleichung, in der nur noch die Endwinkelgeschwindigkeit unbekannt ist |
|||
:<math>r=\frac{J(\omega_a-\omega_e)}{mr\omega_e}</math> |
|||
Die Walze bewegt sich im Endzustand mit |
|||
:<math>\omega_e=\frac{J}{J+mr^2}</math> = 101 1/s und <math>v_e=r\omega_e</math> =6.06 m/s |
|||
4.) Die dissipierte Energie ist gleich der vom [[Drehimpuls]] frei gesetzten minus der vom [[Impuls]] aufgenommenen Energie (auch hier hilft das [[Flüssigkeitsbild]], die richtige Beziehung zu formulieren) |
|||
:<math>W_{diss}=-\Delta L \overline\omega-\Delta p\overline v=(\omega_a-\omega_e)J\frac{\omega_a+\omega_e}{2}-\frac m2 v_e^2</math> = 218 J |
|||
== Lösung zu Aufgabe 7 == |
|||
1.) Das Wasser muss zuerst um 15°C gekühlt und dann zu Eis gefroren werden. Dabei gibt es Energie in Form von Wärme |
|||
:<math>W_{th}=\Delta H = m(c\Delta T-q)</math> = -1.587 GJ |
|||
und Entropie ab |
|||
:<math>S_{aus}=\Delta S=m\left(c\ln\left(\frac{T_2}{T_1}\right)-\frac{q}{T_2}\right)</math> = -5.788 MJ/K |
|||
2.) Die [[Wärmepumpe]] muss mehr Entropie fördern als das Wasser abgegeben hat, weil die Entropie auf dem Weg durch den Gefrierraum zunimmt. Die Energie bleibt dagegen erhalten. Bilanziert man die Entropie an der Schnittstelle zur Wärmepumpe, berechnet sich die Entropie aus der thermischen Energie und der dort herrschenden Temperatur |
|||
:<math>S=\frac{W_{th}}{T_u}</math> = 6.034 MJ/K |
|||
Diese Entropie muss nun um 50 K hoch gepumpt werden |
|||
:<math>W=\Delta T S</math> = 302 MJ |
|||
3.) Der Zuwachs an Entropie in der Umgebung ist gleich der thermisch aufgenommenen Energie dividiert durch die Temperatur der Umgebung |
|||
:<math>\Delta S_{Um}=\frac{\left|\Delta H\right|+W}{T_{Um}}</math> = 6.339 MJ/K |
|||
Die insgesamt produzierte Entropie ist dann gleich der Differenz zwischen der von der Umwelt aufgenommenen und der vom Wasser abgegebenen Menge |
|||
:<math>S_{prod}=\Delta S_{Um}-\left|\Delta S\right|</math> = 0.55 MJ/K |
|||
4.) Unter idealen Bedingungen (reversible Prozessführung) ist die von der Umwelt aufgenommene Entropie gleich der vom Wasser abgegeben Entropie. Die von einer idealen Wärmepumpe zuzuführende Energie ist dann gleich der Differenz zwischen der von der Entropie an die Umwelt abgeschleppten und der aus dem Wasser stammenden Energie |
|||
:<math>W=W_{th_{Um}}-\left|\Delta H\right|=T_{Um}\left|\Delta S\right|-\left|\Delta H\right|</math> = 1.725 GJ - 1.587 GJ = 138 MJ |
|||
== Lösung zu Aufgabe 8 == |
|||
1.) und 2.) Die entsprechenden Diagramme finden Sie beim [[Joule-Zyklus]]. |
|||
3.) Bei der isentropen Kompression eines [[ideales Gas|idealen Gases]] steigt die Temperatur gemäss folgender Gesetzmässigkeit |
|||
:<math>T_2=T_1\left(\frac{V_1}{V_2}\right)^{\kappa-1}</math> = 220 K * 40<sup>0.4</sup> = 962 K (689°C) |
|||
4.) Bei der isentropen Kompression ist die Kompressionsarbeit gleich der Änderung der inneren Energie |
|||
:<math>\hat w=\hat c_V\Delta T</math> = 15.4 kJ/mol |
|||
== Lösung zu Aufgabe 9 == |
|||
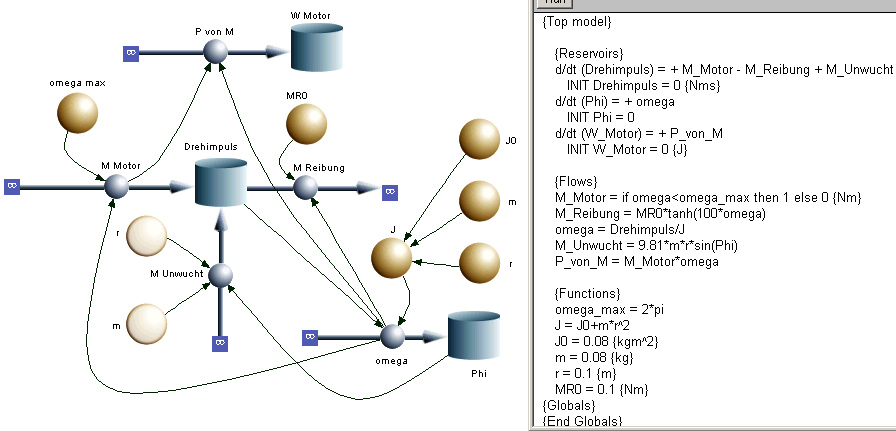
Nachfolgend das [[Systemdiagramm]] (flowchart) sowie die Gleichungen. |
|||
[[Bild:Ass06_L9.jpg]] |
|||
'''[[Aviatik 2006/Ass|Aufgabe]]''' |
|||
Aktuelle Version vom 28. Juli 2008, 07:07 Uhr
Jede Aufgabe wird mit 4 Punkten bewertet.
Lösung zu Aufgabe 1
1.) Die Stärke des Volumenstromes beträgt 0.0133 m3/s. Dies ergibt bei einem Druckunterschied über der Pumpe von 6.5 bar eine Prozessleistung von
- [math]P=\Delta pI_V[/math] = 6.5*105 * 0.0133 m3/s = 8.67 kW
2.) Bei der turbulente Strömung nimmt der Druck quadratisch mit der Volumenstromstärke zu
- [math]\Delta p=kI_V^2[/math]
Aus den gegebenen Daten berechnet sich die Konstante für einen Leitungsabschnitt von 300 m auf k = 2.025*109 Pas2/m6. Die in diesem Abschnitt dissipierte Leistung ist folglich gleich
- [math]P=\Delta pI_V=kI_V^3[/math] = 2.025 kW
3.) Die Stärke eines linear anschwellenden Stromes kann wir folgt beschrieben werden
- [math]I_V=at[/math] mit a = 1.667*10-3 m3/s2
Nun kann die dissipierte Energie als Zeitintegral aus der dissipierten Leistung berechnet werden
- [math]W=\int Pdt=\int kI_V^3dt=\int ka^3t^3=\frac k4 a^3t^4[/math] = 9.6 kJ
Lösung zu Aufgabe 2
1.) Zum Zeitnullpunkt fliesst der Strom durch den Widerstand 1 und durch den Kondensator (ein ungeladener Kondensator verhält sich wie ein Kurzschluss). Deshalb liegt anfänglich die volle Spannung von 6 V über dem ersten Widerstand. Über dem zweiten Widerstand ist dann die Spannung gleich Null. 40 ms später ist der Kondensator geladen und lässt keinen Strom mehr durch. Der Strom fliesst dann nacheinander durch die beiden Widerstände, welche die Spannung von 6V entsprechend ihrer Grösse aufteilen.
2.) Zum Zeitnullpunkt setzt sich nur der erste Widerstand der Spannung entgegen
- [math]R_1=\frac{U_0}{I}[/math] = 6V / 0.03A = 200Ω
Im stationären Zustand fliesst bei einer Gesamtspannung von 6 V ein Strom von 20 mA durch beide Widerstände. Folglich beträgt der totale Widerstand
- [math]R_{tot}=\frac{U_0}{I}[/math] = 300Ω
Weil der erste Widerstand eine Grösse von 200Ω aufweist, muss der zweite einen Wert von 100Ω haben. Die beiden Widerstände teilen dann die angelegte Spannung im Verhältnis 2:1 (4 V und 2 V).
3.) Zum Zeitnullpunkt wird am meisten Leistung diessipiert (kleinster Gesamtwiderstand bei gegebener Spannung)
- [math]P=UI=RI^2[/math] = 0.18 W
4.) Die Grösse der Kapazität kann auf zwei Arten abgeschätzt werden:
- In der ersten Vorgehensweise bestimmt man die auf den Kondensator geflossene Ladung. Diese ergibt sich als Differenz zwischen der durch den Widerstand 1 und der durch den Widerstand 2 geflossene Ladung (Flächen unter der Strom-Zeit-Kurve). Dividiert man diese Ladung durch die Endspannung von 2 V, erhält man eine Kapazität von 100μF.
- Im zweiten Verfahren bestimmt man die Zeitkonstante beim Entladen des Kondensators (Tangente an einen beliebigen Punkt der Kurve und Schnittpunkt mit der Nulllinie bestimmen; die Zeitkonstante ist dann gleich dem zugehörigen Abschnitt auf der Zeitachse). Bei einem RC-Glied ist die Zeitkonstante gleich Widerstand mal Kapazität(τ = RC).
Lösung zu Aufgabe 3
Das Geschwindigkeits-Zeit-Diagramm entspricht dem Füllhöhen-Zeit-Diagramm im Flüssigkeitsbild.
1.) Im Flüssigkeitsbild wird der elastische Stoss als vollständiges "Überschwingen" der beiden Wassersäulen dargestellt. Der schwere Wagen (auflaufender oder Hammerwagen) würde sich nach dem Stoss mit 0.6 m/s und der leichtere Ambosswagen mit 3.6 m/s vorwärts bewegen.
2.) Die Steigung der v-t-Kurve entspricht der Beschleunigung (-2 m/s2). Multipliziert man diese mit der Masse, erhält man die Impulsänderungsrate (-80 kN). Diese Rate entspricht der resultierenden Kraft. Diese setzt sich hier nur aus der Reibungskraft zusammen (80 kN entgegen der Bewegungsrichtung).
3.) Die Verschiebung des Wagens entspricht der zugehörigen Fläche unter dem Geschwindigkeits-Zeit-Diagramm (2.3 m).
4.) Die dissipierte Energie entspricht in dieser Zeitspanne der Änderung der kinetischen Energie des auflaufenden Wagens (Hammerwagen). Im fraglichen Zeitabschnitt ändert der schwerere Wagen seine Geschwindigkeit von 0.93 m/s auf 1.5 m/s
- [math]W_{diss}=\Delta W_{kin}=\frac m2\left(v_{vor}^2-v_{nach}^2\right)[/math] = 25.4 kJ
Lösung zu Aufgabe 4
1.) Die Vertikalbeschleunigung zu Beginn des Loopings entspricht gerade der Normalbeschleunigung auf der Kreisbahn
- [math]a_n=\frac {v^2}{r}[/math] = 26.1 m/s2
2.) Auf das Flugzeug wirken nur das Gravitationsfeld und die Luft ein. Aus der Impulsbilanz in vertikaler Richtung (positive Richtung nach oben)
- [math]F_L-F_G=\dot p=m\dot v=ma_n[/math]
folgt deshalb
- [math]F_L=F_G+ma_n=m(g+a_n)[/math] = 108 kN
3.) Am höchsten Punkt der Bahn beträgt die Radialbeschleunigung infolge kleinerer Geschwindigkeit nur noch 4.8 m/s2 (nach unten). Geht man ins mitbeschleunigte System Flugzeug, misst man eine lokale Gravitationsfeldstärke von
- [math]g'=g-g_t[/math] = 10 N/kg - 4.8 N/kg =5.2 N/kg (nach unten)
Weil die Beschleunigung des Flugzeuges (Bezugssystem) nach unten gerichtet ist, zeigt das Trägheitsfeld mit der Stärke gt nach oben. Relativ zum Flugzeug ist der Pilot im Gleichgewicht, also müssen die Gurten den Piloten mit
- [math]F_{Gurt}=F'_G=mg'[/math] = 390 N
nach oben ziehen
4.) Diese vergleichende Zusatzaufgabe löst man am einfachsten über eine Energiebilanz zu zwei Zeitpunkten
- [math]W_{G1}+W_{kin1}=W_{G2}+W_{kin3}[/math] oder [math]\Delta W_G +\Delta W_{kin}=0[/math]
Wählt man den Bezugspunkt für die Höhe bei 1 und schreibt für die Höhe 2 einfach nur h, erhält man
- [math]\frac m2 v_1^2=mgh+\frac m2 v_2^2[/math]
Daraus folgt
- [math]h=\frac{v_1^2-v_2^2}{2g}[/math] = 800 m
Lösung zu Aufgabe 5
1.) Im Horizontalflug kompensieren sich Auftriebs- und Gewichtskraft (vertikal) sowie Schub- und Luftwiderstandskraft (horizontal). Folglich ist das Verhältnis von Widerstand zu Auftrieb gleich dem Verhältnis von Gewicht (2.4 MN) zu Schub (4 * 40 kN = 160 kN), also gleich 1:15.
2.) Nimmt man an, dass die Luft ungehindert in die Öffnung eines Triebwerk eindringt, ergibt sich für den Massenstrom
- [math]I_m=\varrho I_V=\varrho A v[/math] = 232 kg/s
3.) Im stationären Betrieb ist die Schubkraft (leitungsartig an das Flugzeug abfliessender Impulsstrom) gleich der Impulsänderungsrate des durchfliessenden Massenstromes
- [math]F_S=(v_2-v_1)I_m[/math]
Daraus folgt für die Geschwindigkeit der austretenden Gase
- [math]v_2=\frac{F_S}{I_m}+v_1[/math] = 412 m/s
4.) Die im Triebwerk auf den Gasstrom aufgeladen Leistung ist gleich der Differenz der beiden (kinetischen) Energieströme
- [math]P=I_{W_{kin2}}-I_{W_{kin1}}=\left(v_2^2-v_1^2\right)\frac{I_m}{2}=\overline v F_S[/math] = 13 MW
Lösung zu Aufgabe 6
Diese Aufgabe ist mit dem Problem der Bowling-Kugel verwandt.
1.) Auf den rotierenden Zylinder wirken die Gewichtskraft (nach unten), die Normalkraft (nach oben) sowie die Gleitreibungskraft (nach vorn).
2.) Der Impulstopf (Grundfläche m) ist anfänglich leer und füllt sich dann unter der Wirkung der Gleitreibungskraft FR bis zur Endgeschwindigkeit ve. Der Drehimpulstopf (Grundfläche J) ist anfänglich bis ωa gefüllt. Unter der Wirkung des Drehmoments der Gleitreibungskraft (M=r*FR) sinkt dessen Niveau auf ωe ab.
3.) Das Verhältnis zwischen Drehimpulsänderung und Impulsänderung ist gleich dem Verhältnis zwischen Drehmoment und Kraft (die beiden Inhaltsänderungen sind gleich gekoppelt wie die zugehörigen Ströme)
- [math]\frac{rF_r}{F_R}=\frac{\Delta L}{\Delta p}=\frac{J(\omega_a-\omega_e)}{mv_e}[/math]
Nun ist die Endgeschwindigkeit über die Rollbedingung mit der Endwinkelgeschwindigkeit verknüpft. Setzt man diese Rollbedingung [math]\left(v_e=r\omega_e\right)[/math] ein, erhält man eine Gleichung, in der nur noch die Endwinkelgeschwindigkeit unbekannt ist
- [math]r=\frac{J(\omega_a-\omega_e)}{mr\omega_e}[/math]
Die Walze bewegt sich im Endzustand mit
- [math]\omega_e=\frac{J}{J+mr^2}[/math] = 101 1/s und [math]v_e=r\omega_e[/math] =6.06 m/s
4.) Die dissipierte Energie ist gleich der vom Drehimpuls frei gesetzten minus der vom Impuls aufgenommenen Energie (auch hier hilft das Flüssigkeitsbild, die richtige Beziehung zu formulieren)
- [math]W_{diss}=-\Delta L \overline\omega-\Delta p\overline v=(\omega_a-\omega_e)J\frac{\omega_a+\omega_e}{2}-\frac m2 v_e^2[/math] = 218 J
Lösung zu Aufgabe 7
1.) Das Wasser muss zuerst um 15°C gekühlt und dann zu Eis gefroren werden. Dabei gibt es Energie in Form von Wärme
- [math]W_{th}=\Delta H = m(c\Delta T-q)[/math] = -1.587 GJ
und Entropie ab
- [math]S_{aus}=\Delta S=m\left(c\ln\left(\frac{T_2}{T_1}\right)-\frac{q}{T_2}\right)[/math] = -5.788 MJ/K
2.) Die Wärmepumpe muss mehr Entropie fördern als das Wasser abgegeben hat, weil die Entropie auf dem Weg durch den Gefrierraum zunimmt. Die Energie bleibt dagegen erhalten. Bilanziert man die Entropie an der Schnittstelle zur Wärmepumpe, berechnet sich die Entropie aus der thermischen Energie und der dort herrschenden Temperatur
- [math]S=\frac{W_{th}}{T_u}[/math] = 6.034 MJ/K
Diese Entropie muss nun um 50 K hoch gepumpt werden
- [math]W=\Delta T S[/math] = 302 MJ
3.) Der Zuwachs an Entropie in der Umgebung ist gleich der thermisch aufgenommenen Energie dividiert durch die Temperatur der Umgebung
- [math]\Delta S_{Um}=\frac{\left|\Delta H\right|+W}{T_{Um}}[/math] = 6.339 MJ/K
Die insgesamt produzierte Entropie ist dann gleich der Differenz zwischen der von der Umwelt aufgenommenen und der vom Wasser abgegebenen Menge
- [math]S_{prod}=\Delta S_{Um}-\left|\Delta S\right|[/math] = 0.55 MJ/K
4.) Unter idealen Bedingungen (reversible Prozessführung) ist die von der Umwelt aufgenommene Entropie gleich der vom Wasser abgegeben Entropie. Die von einer idealen Wärmepumpe zuzuführende Energie ist dann gleich der Differenz zwischen der von der Entropie an die Umwelt abgeschleppten und der aus dem Wasser stammenden Energie
- [math]W=W_{th_{Um}}-\left|\Delta H\right|=T_{Um}\left|\Delta S\right|-\left|\Delta H\right|[/math] = 1.725 GJ - 1.587 GJ = 138 MJ
Lösung zu Aufgabe 8
1.) und 2.) Die entsprechenden Diagramme finden Sie beim Joule-Zyklus.
3.) Bei der isentropen Kompression eines idealen Gases steigt die Temperatur gemäss folgender Gesetzmässigkeit
- [math]T_2=T_1\left(\frac{V_1}{V_2}\right)^{\kappa-1}[/math] = 220 K * 400.4 = 962 K (689°C)
4.) Bei der isentropen Kompression ist die Kompressionsarbeit gleich der Änderung der inneren Energie
- [math]\hat w=\hat c_V\Delta T[/math] = 15.4 kJ/mol
Lösung zu Aufgabe 9
Nachfolgend das Systemdiagramm (flowchart) sowie die Gleichungen.