Erzwungene Kreisbewegung: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) (→Modell) |
Admin (Diskussion | Beiträge) |
||
| (6 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Ein Körper, der sich auf einer [[Kreisbewegung|Kreisbahn]] bewegt, muss mit der Umgebung andauernd [[Impuls]] austauschen. Die Impulsänderungsrate |
Ein Körper, der sich auf einer [[Kreisbewegung|Kreisbahn]] bewegt, muss mit der Umgebung andauernd [[Impuls]] austauschen, damit er die Kurve kriegt. Die Impulsänderungsrate entspricht der resultierenden [[Kraft]] auf den Körper. Die Normalkomponente dieser resultierenden Kraft zeigt gegen die Mitte des Kreises und ändert nur die Bewegungsrichtung des Körpers. Die Tangentialkomponente beeinflusst dagegen die [[Schnelligkeit]]. |
||
Schüler und leider auch Studierende haben Mühe, die Kreisbewegung physikalisch zu verstehen. Als Ursache für diese Schwierigkeiten kommen mehrere Faktoren in Frage |
|||
*der Zusammenhang zwischen [[Kraft]], [[Impuls]] und [[Energie]] wird nicht durchschaut |
*der Zusammenhang zwischen [[Kraft]], [[Impuls]] und [[Energie]] wird nicht durchschaut |
||
*die Kreisbewegung wird als nicht beschleunigt empfunden, weil die [[kinetische Energie]] erhalten bleibt |
*die Kreisbewegung wird als nicht beschleunigt empfunden, weil die [[kinetische Energie]] erhalten bleibt |
||
*der Begriff der Beschleunigung als Ableitung eines Vektors (der Geschwindigkeit) nach der Zeit ist zu abstrakt |
*der Begriff der Beschleunigung als Ableitung eines Vektors (der Geschwindigkeit) nach der Zeit ist zu abstrakt |
||
*der Austausch von Impuls mit der Erde |
*der Austausch von Impuls mit der Erde wird nicht als solcher wahrgenommen, weil keine Energie mit transportiert wird. |
||
==Modell== |
==Modell== |
||
[[Bild:ErzwungeneKreisbewegung SD.jpg|thumb|Systemdiagramm]]Die Kreisbewegung dynamisch zu modellieren ist eine Alternative zum klassischen Weg über die [[Newtonsche Axiome|Newtonschen Axiome]] mit Zentralkraft sowie Zentral- oder Normalbeschleunigung. Unser System bestehe aus einem Klotz, der sich |
[[Bild:ErzwungeneKreisbewegung SD.jpg|thumb|Systemdiagramm]]Die Kreisbewegung dynamisch zu modellieren ist eine Alternative zum klassischen Weg über die [[Newtonsche Axiome|Newtonschen Axiome]] mit Zentralkraft sowie Zentral- oder Normalbeschleunigung. Unser System bestehe aus einem Klotz, der sich an einem elastischen Seil um einen Pflock bewegt. Die Reibung in der Gleitschicht zwischen Klotz und Unterlage sowie in der Seilführung wird vernachlässigt. Das Seil verhalte sich wie eine ideale Feder, d.h. die Seilkraft nimmt linear mit der Dehnung, der Verlängerung gegenüber dem nicht gespannten Zustand, zu. |
||
Das [[Systemdiagramm]] zeigt die Struktur des Modells mit den beiden Impulsbilanzen, sowie die kinematische Integration für die ''x''- und die ''y''-Richtung. Die Dehnung |
Das [[Systemdiagramm]] zeigt die Struktur des Modells mit den beiden Impulsbilanzen, sowie die kinematische Integration für die ''x''- und die ''y''-Richtung. Die Dehnung des Seils ist gleich der Differenz zwischen dem momentanen Radius (Abstand des Klotzes vom Nullpunkt) und der Länge des unbelasteten Seils. Die zugehörige Kraft muss danach in eine ''x''- und eine ''y''-Komponente zerlegt werden. |
||
==Simulation== |
==Simulation== |
||
[[Bild:erzwungendeKreisbewegung_Bahn.png|thumb|drei verschiedene Bahnen]]Die Anfanswerte der ''y''-Koordinate und der ''x''-Komponente der Geschwindigkeit können gleich Null gesetzt werden. Der Klotz erhält in ''y''-Richtung eine Geschwindigkeit von 5 m/s. Die Graphik zeigt die Bahn des Klotzes für drei verschiedene Anfangswert |
[[Bild:erzwungendeKreisbewegung_Bahn.png|thumb|drei verschiedene Bahnen]]Die Anfanswerte der ''y''-Koordinate und der ''x''-Komponente der Geschwindigkeit können gleich Null gesetzt werden. Der Klotz erhält in ''y''-Richtung eine Geschwindigkeit von 5 m/s. Die Graphik zeigt die Bahn des Klotzes für drei verschiedene Anfangswert der ''x''-Koordinate. Die schwarze Kurve zeigt die Bahn bei einem Start mit nicht gespanntem Seil (''x<sub>0</sub>'' = 0.5 m). Bei der grünen Kurve ist die Feder anfänglich am stärksten gespannt. Eine Kreisbahn (rote Kurve) ergibt sich nur, wenn Federspannung, Masse, Abstand vom Zentrum sowie Anfangsgeschwindigkeit aufeinander abgestimmt sind. Und dies berechnen wir mit den Formeln, die in keinem Physikunterricht fehlen |
||
:<math>F_n=ma=\frac{mv^2}{l_0+x}=F_{Seil}=Dx</math> |
|||
Die Dehnung des Seils wird hier mit ''x'' bezeichnet, die zugehörige Richtgrösse (Federkonstante) mit ''D''. Die Auswertung dieser Gleichung liefert eine Dehnung von 0.0854 m und somit eine für die Kreisbahn notwendige Seillänge (im Modell als Federlänge bezeichnet) von 0.5854 m, was eine Zentralkraft von 85.4 N ergibt. |
|||
Startet man nicht optimal, führt der Körper in radiale Richtung eine Schwingung aus. |
|||
==Energie== |
|||
[[Bild:ErzwungeneKreisbewegung Energie.jpg|thumb|Teilmodell Energiebilanz]] Die [[Energiebilanz]] bildet neben der [[Impulsbilanz]] und der Kinematik die dritte Ebene in einem Modell zur [[Translationsmechanik]]. Die energetischen Beziehungen lassen sich aus der Impulsbilanz sowie der Geometrie ableiten. Folglich ist die Energie eine Grösse, die keinen Einfluss auf das Geschehen nimmt und rein buchhalterisch nachzuführen ist. |
|||
Der Austausch von Energie zwischen Klotz und elastischen Seil erfolgt über den Impuls: der [[zugeordneter Energiestrom|zugeordnete Energiestrom]] ist gleich dem Skalarprodukt aus Geschwindigkeit und Seilkraft (Impulsstromstärke). Impulsströme und Energiestrom sollten die gleiche Bezugsrichtung aufweisen. In diesem Modell sind alle drei Ströme (Impuls und Energie) positiv, falls sie aus dem Klotz weg fliessen. Nun ist der Energieinhalt eines Körpers gemäss ''Albert Einstein'' gleich seiner Masse mal das Quadrat der Lichtgeschwindigkeit. Weil diese Betrachtung viel zu grosse Werte liefern würde, führt man die Teilenergien '''elastische Energie''' des Seils und '''kinetische Energie des Klotzes''' ein. Diesen Teilenergien wird je ein eigener Nullpunkt zugewiesen. So hat das nicht gespannte Seil keine elastische Energie und der ruhende Körper keine kinetische. Ist das Seil anfänglich gespannt, muss der zugehörige Wert berechnet und als Startwert ins Modell eingegeben werden. Analog verfährt man mit der kinetischen Energie. |
|||
Die elastische Energie ist zu Beginn der Simulation gleich |
|||
:<math>W_{Seil_0}=\frac D2 x_0^2=\frac D2 (r_0-l_0)^2</math> |
|||
und die kinetische |
|||
:<math>W_{kin_0}=\frac m2 (v_{x0}^2+v_{y0}^2)</math> |
|||
[[Kategorie:Trans]] [[Kategorie:TransMod]] [[Kategorie:Modelle]] |
|||
Aktuelle Version vom 29. September 2008, 05:21 Uhr
Ein Körper, der sich auf einer Kreisbahn bewegt, muss mit der Umgebung andauernd Impuls austauschen, damit er die Kurve kriegt. Die Impulsänderungsrate entspricht der resultierenden Kraft auf den Körper. Die Normalkomponente dieser resultierenden Kraft zeigt gegen die Mitte des Kreises und ändert nur die Bewegungsrichtung des Körpers. Die Tangentialkomponente beeinflusst dagegen die Schnelligkeit.
Schüler und leider auch Studierende haben Mühe, die Kreisbewegung physikalisch zu verstehen. Als Ursache für diese Schwierigkeiten kommen mehrere Faktoren in Frage
- der Zusammenhang zwischen Kraft, Impuls und Energie wird nicht durchschaut
- die Kreisbewegung wird als nicht beschleunigt empfunden, weil die kinetische Energie erhalten bleibt
- der Begriff der Beschleunigung als Ableitung eines Vektors (der Geschwindigkeit) nach der Zeit ist zu abstrakt
- der Austausch von Impuls mit der Erde wird nicht als solcher wahrgenommen, weil keine Energie mit transportiert wird.
Modell
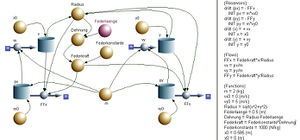
Die Kreisbewegung dynamisch zu modellieren ist eine Alternative zum klassischen Weg über die Newtonschen Axiome mit Zentralkraft sowie Zentral- oder Normalbeschleunigung. Unser System bestehe aus einem Klotz, der sich an einem elastischen Seil um einen Pflock bewegt. Die Reibung in der Gleitschicht zwischen Klotz und Unterlage sowie in der Seilführung wird vernachlässigt. Das Seil verhalte sich wie eine ideale Feder, d.h. die Seilkraft nimmt linear mit der Dehnung, der Verlängerung gegenüber dem nicht gespannten Zustand, zu.
Das Systemdiagramm zeigt die Struktur des Modells mit den beiden Impulsbilanzen, sowie die kinematische Integration für die x- und die y-Richtung. Die Dehnung des Seils ist gleich der Differenz zwischen dem momentanen Radius (Abstand des Klotzes vom Nullpunkt) und der Länge des unbelasteten Seils. Die zugehörige Kraft muss danach in eine x- und eine y-Komponente zerlegt werden.
Simulation
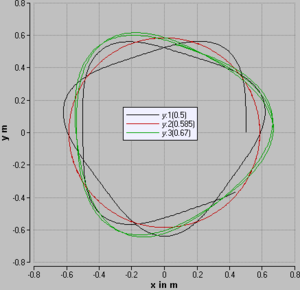
Die Anfanswerte der y-Koordinate und der x-Komponente der Geschwindigkeit können gleich Null gesetzt werden. Der Klotz erhält in y-Richtung eine Geschwindigkeit von 5 m/s. Die Graphik zeigt die Bahn des Klotzes für drei verschiedene Anfangswert der x-Koordinate. Die schwarze Kurve zeigt die Bahn bei einem Start mit nicht gespanntem Seil (x0 = 0.5 m). Bei der grünen Kurve ist die Feder anfänglich am stärksten gespannt. Eine Kreisbahn (rote Kurve) ergibt sich nur, wenn Federspannung, Masse, Abstand vom Zentrum sowie Anfangsgeschwindigkeit aufeinander abgestimmt sind. Und dies berechnen wir mit den Formeln, die in keinem Physikunterricht fehlen
- [math]F_n=ma=\frac{mv^2}{l_0+x}=F_{Seil}=Dx[/math]
Die Dehnung des Seils wird hier mit x bezeichnet, die zugehörige Richtgrösse (Federkonstante) mit D. Die Auswertung dieser Gleichung liefert eine Dehnung von 0.0854 m und somit eine für die Kreisbahn notwendige Seillänge (im Modell als Federlänge bezeichnet) von 0.5854 m, was eine Zentralkraft von 85.4 N ergibt.
Startet man nicht optimal, führt der Körper in radiale Richtung eine Schwingung aus.
Energie
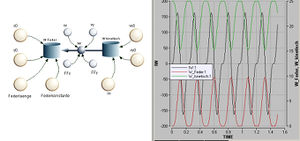
Die Energiebilanz bildet neben der Impulsbilanz und der Kinematik die dritte Ebene in einem Modell zur Translationsmechanik. Die energetischen Beziehungen lassen sich aus der Impulsbilanz sowie der Geometrie ableiten. Folglich ist die Energie eine Grösse, die keinen Einfluss auf das Geschehen nimmt und rein buchhalterisch nachzuführen ist.
Der Austausch von Energie zwischen Klotz und elastischen Seil erfolgt über den Impuls: der zugeordnete Energiestrom ist gleich dem Skalarprodukt aus Geschwindigkeit und Seilkraft (Impulsstromstärke). Impulsströme und Energiestrom sollten die gleiche Bezugsrichtung aufweisen. In diesem Modell sind alle drei Ströme (Impuls und Energie) positiv, falls sie aus dem Klotz weg fliessen. Nun ist der Energieinhalt eines Körpers gemäss Albert Einstein gleich seiner Masse mal das Quadrat der Lichtgeschwindigkeit. Weil diese Betrachtung viel zu grosse Werte liefern würde, führt man die Teilenergien elastische Energie des Seils und kinetische Energie des Klotzes ein. Diesen Teilenergien wird je ein eigener Nullpunkt zugewiesen. So hat das nicht gespannte Seil keine elastische Energie und der ruhende Körper keine kinetische. Ist das Seil anfänglich gespannt, muss der zugehörige Wert berechnet und als Startwert ins Modell eingegeben werden. Analog verfährt man mit der kinetischen Energie.
Die elastische Energie ist zu Beginn der Simulation gleich
- [math]W_{Seil_0}=\frac D2 x_0^2=\frac D2 (r_0-l_0)^2[/math]
und die kinetische
- [math]W_{kin_0}=\frac m2 (v_{x0}^2+v_{y0}^2)[/math]