Druckgesetz der Hydrostatik: Unterschied zwischen den Versionen

Inhalt hinzugefügt Inhalt gelöscht

Inline

Aktuelle Version vom 5. Dezember 2009, 16:11 Uhr

Der Druck in einer ruhenden Flüssigkeit nimmt durch die Wirkung des Gravitationsfeldes mit der Eintauchtiefe zu. Diese Druckzunahme wird durch das Druckgesetz der Hydrostatik beschrieben.

homogenes Gravitationsfeld

Das Druckgesetz der Hydrostatik kann mit Hilfe einer Energiebilanz formuliert werden. Dazu wählt man zwei Punkt in der Flüssigkeit aus und denkt sich eine ganz langsame Strömung von Punkt eins nach Punkt zwei. Diese Strömung soll so klein sein, dass sie praktisch keine Reibung verursacht und fast keine kinetische Energie benötigt. Dann gelten die Voraussetzungen des Gesetzes von Bernoulli:

[math]\left(\frac{\varrho}{2}v_1^2+\varrho gh_1+p_1\right)I_V{_1}+\left(\frac{\rho}{2}v_2^2+\rho gh_2+p_2\right)I_V{_2}=0[/math]

Nun lässt man die Strömungsgeschwindigkeit gegen Null gehen und löst diese Beziehung nach dem Druck in Punkt zwei auf

[math]p_2=p_1+\varrho g(h_1-h_2)= p_1+\varrho g\Delta h[/math]

Der Druck in einer Flüssigkeit steigt proportional zur Eintauchtiefe, wobei der Proportionalitätsfaktor gleich Dichte mal Gravitationsfeldstärke ist. Im häufigsten Fall, beim Eintauchen in Wasser, nimmt der Druck pro zehn Meter Wassertiefe um ein paar zu.

Zentrifugalfeld

Die allgemeine Form des Gesetzes von Bernoulli lautet

[math]\frac {\varrho}{2} v_1^2 + \rho \varphi_G + p_1 = \frac {\varrho}{2} v_2^2 + \varrho \varphi_G + p_2 [/math]

Setzt man die Geschwindigkeiten gleich Null (ruhende Flüssigkeit) und löst die Gleichung nach dem Druck im Punkt zwei auf, gewinnt man die allgemeine Druckformel für Flüssigkeiten in einem Gravitationsfeld

[math]p_2 = p_1 + \varrho (\varphi_{G1} - \varphi_{G2}) = p_1 + \varrho \Delta \varphi_G[/math]

Die Druckänderung in einer ruhenden Flüssigkeit ist gleich Dichte mal die Änderung des Gravitationspotenzials. Folglich weisen Punkte, die auf einer Äquipotenzialfläche des Gravitationsfeldes liegen, den gleichen Druck auf.

Setzt man in diese Formel das Gravitationspotenzial eines Zentrifugalfeldes ein, erhält man das Druckgesetz für Flüssigkeiten in einer Zentrifuge

[math]p_2 = p_1 + \varrho \frac {\omega^2}{2}(r_2^2 - r_1^2) = p_1 + \varrho \omega^2 \overline r \Delta r[/math]

Der Druckunterschied in einer Zentrifuge ist proportional zur Dichte der Flüssigkeit, proportional zum Quadrat der Drehzahl, proportional zum mittleren Abstand von der Drehachse und proportional zur radialen Distanz der beiden Punkte.

Himmelskörper

Die Gravitationsfeldstärke im Innern eines radialsymmetrisch aufgebauten Himmelskörpers ist gleich

[math]g(r_0) = \frac {4 \pi G}{r_0^2} \int_0^{r_0} \varrho (r) r^2 dr[/math]

Nimmt man an, dass die Dichte im ganzen Himmelskörper homogen ist, erhält man eine im Himmelskörper linear wachsende Gravitationsfeldstärke

[math]g(r) = \frac {4\pi} {3} \varrho G r[/math]

Setzt man das Gravitationspotenzial im Zentrum des Himmelskörpers gleich Null, nimmt dieses quadratisch mit dem Radius zu

[math]\varphi_G = \frac {2\pi} {3} \varrho G r^2[/math]

Das verallgemeinerte Gesetz von Bernoulli (siehe weiter oben) liefert dann die Druckzunahme im homogenen Himmelskörper

[math]p_2 = p_1 + \frac {2\pi} {3} \varrho G (r_1^2 - r_2^2)[/math]

Bei erdähnlichen Planeten oder Neutronensternen kann mit dieser Formel der Druck im Zentrum mit Hilfe der mittleren Dichte abgeschätzt werden.

hydrostatisches Paradoxon

Den Umstand, wonach die Kraft auf den Gefässboden grösser sein kann als die Gewichtskraft auf die darüber liegenden Flüssigkeit, nennt man hydrostatisches Paradoxon.

Entstehung des Paradoxons

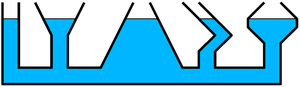
In allen Gefässen mit demselben Füllstand herrscht auf gleicher Höhe unabhängig von der Gefässform derselbe Druck. Die Kraft von der Flüssigkeit auf den Gefässboden (Querschnitt A) ist deshalb unabhängig von der Menge aber proportional zur Höhe h der darüber liegenden Flüssigkeit

[math]F_B = p_B A = (p_0 + \varrho g h) A[/math]

Setzt man dagegen einen Festkörper auf den Boden, fliesst der gravitativ zugeführte Impuls ziemlich homogen verteilt durch die Auflagefläche weg. Der Druck bei der Auflagefläche ist bei einem festen Körper mit eben aufliegender Fläche gleich Gewichtskraft geteilt durch Grösse der Auflagefläche.

Diese Erfahrung und die gutgemeinte Herleitung der hydrostatischen Druckformel mit Hilfe der Gewichtskraft auf die darüberliegende Flüssigkeit, erschweren das Verständnis für die Bodendruckkraft im Innern eines mit Flüssigkeit gefüllten Gefässes. Folgt man der Argumentation, wonach das Gewicht den hydrostatischen Druck erzeugt, versteht man nicht, wieso die Kraft auf die Grundfläche in einem nach oben zulaufenden Gefäss grösser ist, als das Gewicht der ganzen darüberliegenden Flüssigkeit. Daher der Name hydrostatisches Paradoxon.

Erklärung

Eine ruhende Flüssigkeit transportiert an jedem Punkt alle drei Impulskomponenten mit gleicher Stärke in Richtung der zugehörigen Koordinatenachse; der Druck ist der isotrope Anteil der Impulsstromdichte. Wählt man die z-Achse nach unten, fliesst der gravitativ zugeführte Impuls immer nach unten weg. Dies führt im homogenen Gravitationsfeld zur - weiter oben mit Hilfe des Gesetzes von Bernoulli hergeleiteten - linearen Zunahme des Druckes mit der Eintauchtiefe. Infolge des Materialverhaltens der Flüssigkeit, welches die Isotropie der Impulsstromdichte erzwingt, planzt sich der Druck bis zu den begrenzenden Wänden fort (die x- und die y-Impulsströme werden von den Gefässwänden aufgenommen). Folglich gilt die Herleitung der hydrostatischen Druckformel mit Hilfe der Gravitationskraft nur für Punkte unterhalb der freien Oberfläche. Verengt sich das Gefäss nach oben, fliesst dort von oben her, aus den Gefässwänden, ein zusätzlicher z-Impulsstrom, der gerade so stark ist, dass der Druck in der ruhenden Flüssigkeit auf gleicher Höhe überall gleich gross ist.

Hat das Gefäss die Form einer Schraubenfeder, besteht kein direkter Zusammenhang mehr zwischen gravitativ zugeführtem Impuls (Gewichtskraft) und Impulsstromstärke bei der Grenzfläche zwischen der Flüssigkeit und dem Gefässboden (Bodendruckkraft). Bei dermassen verdrehten Gefässen fliesst der gravitativ zugeführte z-Impuls auf seinem Weg nach unten abwechselnd durch die Flüssigkeit und die Gefässwände.

@@ Zeile 4: / Zeile 4: @@
 Das Druckgesetz der Hydrostatik kann mit Hilfe einer [[Energiebilanz]] formuliert werden. Dazu wählt man zwei Punkt in der Flüssigkeit aus und denkt sich eine ganz langsame Strömung von Punkt eins nach Punkt zwei. Diese Strömung soll so klein sein, dass sie praktisch keine Reibung verursacht und fast keine kinetische Energie benötigt. Dann gelten die Voraussetzungen des [[Gesetz von Bernoulli|Gesetzes von Bernoulli]]:
-:<math>\left(\frac {\rho}{2} v_1^2 + \rho g h_1 + p_1 \right) I_V{_1}  + \left(\frac {\rho}{2} v_2^2 + \rho g h_2 + p_2 \right) I_V_2 = 0 </math>
+:<math>\left(\frac{\varrho}{2}v_1^2+\varrho gh_1+p_1\right)I_V{_1}+\left(\frac{\rho}{2}v_2^2+\rho gh_2+p_2\right)I_V{_2}=0</math>
 Nun lässt man die Strömungsgeschwindigkeit gegen Null gehen und löst diese Beziehung nach dem Druck in Punkt zwei auf
-:<math>p_2 = p_1 + \rho g (h_1 - h_2) = p_1 + \rho g \Delta h</math>
+:<math>p_2=p_1+\varrho g(h_1-h_2)= p_1+\varrho g\Delta h</math>
 Der Druck in einer Flüssigkeit steigt proportional zur Eintauchtiefe, wobei der Proportionalitätsfaktor gleich Dichte mal [[Gravitationsfeld]]stärke ist. Im häufigsten Fall, beim Eintauchen in Wasser, nimmt der Druck pro zehn Meter Wassertiefe um ein paar zu.
@@ Zeile 15: / Zeile 15: @@
 Die allgemeine Form des [[Gesetz von Bernoulli|Gesetzes von Bernoulli]] lautet
-:<math>\frac {\rho}{2} v_1^2 + \rho \varphi_G + p_1  = \frac {\rho}{2} v_2^2 + \rho \varphi_G + p_2 </math>
+:<math>\frac {\varrho}{2} v_1^2 + \rho \varphi_G + p_1  = \frac {\varrho}{2} v_2^2 + \varrho \varphi_G + p_2 </math>
 Setzt man die Geschwindigkeiten gleich Null (ruhende Flüssigkeit) und löst die Gleichung nach dem Druck im Punkt zwei auf, gewinnt man die allgemeine Druckformel für Flüssigkeiten in einem [[Gravitationsfeld]]
-:<math>p_2 = p_1 + \rho (\varphi_{G1} - \varphi_{G2}) = p_1 + \rho \Delta \varphi_G</math>
+:<math>p_2 = p_1 + \varrho (\varphi_{G1} - \varphi_{G2}) = p_1 + \varrho \Delta \varphi_G</math>
 Die Druckänderung in einer ruhenden Flüssigkeit ist gleich Dichte mal die Änderung des Gravitationspotenzials. Folglich weisen Punkte, die auf einer Äquipotenzialfläche des Gravitationsfeldes liegen, den gleichen Druck auf.
@@ Zeile 25: / Zeile 25: @@
 Setzt man in diese Formel das Gravitationspotenzial eines Zentrifugalfeldes ein, erhält man das Druckgesetz für Flüssigkeiten in einer Zentrifuge
-:<math>p_2 = p_1 + \rho \frac {\omega^2}{2}(r_2^2 - r_1^2) = p_1 + \rho  \omega^2 \overline r \Delta r</math>
+:<math>p_2 = p_1 + \varrho \frac {\omega^2}{2}(r_2^2 - r_1^2) = p_1 + \varrho  \omega^2 \overline r \Delta r</math>
 Der Druckunterschied in einer Zentrifuge ist proportional zur Dichte der Flüssigkeit, proportional zum Quadrat  der Drehzahl, proportional zum mittleren Abstand von der Drehachse und proportional zur radialen Distanz der beiden Punkte.
@@ Zeile 32: / Zeile 32: @@
 Die Gravitationsfeldstärke im Innern eines radialsymmetrisch aufgebauten Himmelskörpers ist gleich
-:<math>g(r_0) = \frac {4 \pi G}{r_0^2} \int_0^{r_0} \rho (r) r^2 dr</math>
+:<math>g(r_0) = \frac {4 \pi G}{r_0^2} \int_0^{r_0} \varrho (r) r^2 dr</math>
 Nimmt man an, dass die Dichte im ganzen Himmelskörper homogen ist, erhält man eine im Himmelskörper linear wachsende Gravitationsfeldstärke
-:<math>g(r) = \frac {4\pi} {3} \rho G r</math>
+:<math>g(r) = \frac {4\pi} {3} \varrho G r</math>
 Setzt man das Gravitationspotenzial im Zentrum des Himmelskörpers gleich Null, nimmt dieses quadratisch mit dem Radius zu
-:<math>\varphi_G = \frac {2\pi} {3} \rho G r^2</math>
+:<math>\varphi_G = \frac {2\pi} {3} \varrho G r^2</math>
 Das verallgemeinerte Gesetz von Bernoulli (siehe weiter oben) liefert dann die Druckzunahme im homogenen Himmelskörper
-:<math>p_2 = p_1 + \frac {2\pi} {3} \rho G (r_1^2 - r_2^2)</math>
+:<math>p_2 = p_1 + \frac {2\pi} {3} \varrho G (r_1^2 - r_2^2)</math>
 Bei erdähnlichen Planeten oder [[Neutronenstern]]en kann mit dieser Formel der Druck im Zentrum mit Hilfe der mittleren [[Dichte]] abgeschätzt werden.
@@ Zeile 53: / Zeile 53: @@
 ===Entstehung des Paradoxons===
 [[Bild:kommunizierende_Gefaesse2.png|thumb|kommunizierende Gefässe]]
-In allen Gefässen mit demselben Füllstand herrscht auf gleicher Höhe unabhängig von der Gefässform derselbe Druck. Die Kraft von der Flüssigkeit auf den Gefässboden (Querschnitt ''A'') ist deshalb unabhängig von der Menge aber proportional zur Höhe ''h'' der darüber liegenden Flüssigkeit gleich
+In allen Gefässen mit demselben Füllstand herrscht auf gleicher Höhe unabhängig von der Gefässform derselbe Druck. Die Kraft von der Flüssigkeit auf den Gefässboden (Querschnitt ''A'') ist deshalb unabhängig von der Menge aber proportional zur Höhe ''h'' der darüber liegenden Flüssigkeit
-<math>F_B = p_B A = (p_0 + \rho g h) A</math>
+<math>F_B = p_B A = (p_0 + \varrho g h) A</math>
-Setzt man dagegen einen Festkörper auf den Boden, fliesst der gravitativ zugeführte Impuls ziemlich homogen verteilt durch die Auflagefläche weg. Der Druck bei der Auflagefläche ist deshalb gleich Gewichtskraft geteilt durch Grösse der Auflagefläche.
+Setzt man dagegen einen Festkörper auf den Boden, fliesst der gravitativ zugeführte Impuls ziemlich homogen verteilt durch die Auflagefläche weg. Der Druck bei der Auflagefläche ist bei einem festen Körper mit eben aufliegender Fläche gleich Gewichtskraft geteilt durch Grösse der Auflagefläche.
-Diese Erfahrung und die gutgemeinte Herleitung der hydrostatischen Druckformel mit Hilfe der Gewichtskraft auf die darüberliegende Flüssigkeit, erschweren das Verständnis für die Bodendruckkraft im Innern eines mit Flüssigkeit gefüllten Gefässes. Folgt man der Argumentation, wonach das [[Gewicht]] den hydrostatischen Druck erzeugt, versteht man nicht, wieso die [[Kraft]] auf die Grundfläche in einem nach oben zulaufenden Gefäss grösser ist, als das Gewicht der ganzen darüberliegenden Flüssigkeit. Daher der Name Paradoxon.
+Diese Erfahrung und die gutgemeinte Herleitung der hydrostatischen Druckformel mit Hilfe der Gewichtskraft auf die darüberliegende Flüssigkeit, erschweren das Verständnis für die Bodendruckkraft im Innern eines mit Flüssigkeit gefüllten Gefässes. Folgt man der Argumentation, wonach das [[Gewicht]] den hydrostatischen Druck erzeugt, versteht man nicht, wieso die [[Kraft]] auf die Grundfläche in einem nach oben zulaufenden Gefäss grösser ist, als das Gewicht der ganzen darüberliegenden Flüssigkeit. Daher der Name hydrostatisches Paradoxon.
 ===Erklärung===
 Eine ruhende Flüssigkeit transportiert an jedem Punkt alle drei [[Impuls]]komponenten mit gleicher Stärke in Richtung der zugehörigen Koordinatenachse; der Druck ist der isotrope Anteil der [[Impulsstromdichte]]. Wählt man die ''z''-Achse nach unten, fliesst der gravitativ zugeführte Impuls immer nach unten weg. Dies führt im homogenen Gravitationsfeld zur - weiter oben mit Hilfe des [[Gesetz von Bernoulli|Gesetzes von Bernoulli]] hergeleiteten - linearen Zunahme des Druckes mit der Eintauchtiefe. Infolge des Materialverhaltens der Flüssigkeit, welches die Isotropie der Impulsstromdichte erzwingt, planzt sich der Druck bis zu den begrenzenden Wänden fort (die ''x''- und die ''y''-Impulsströme werden von den Gefässwänden aufgenommen). Folglich gilt die Herleitung der hydrostatischen Druckformel mit Hilfe der Gravitationskraft nur für Punkte unterhalb der freien Oberfläche. Verengt sich das Gefäss nach oben, fliesst dort von oben her, aus den Gefässwänden, ein zusätzlicher ''z''-Impulsstrom, der gerade so stark ist, dass der Druck in der ruhenden Flüssigkeit auf gleicher Höhe überall gleich gross ist.
-Hat das Gefäss die Form einer Schraubenfeder, besteht überhaupt kein Zusammenhang mehr zwischen gravitativ zugeführtem Impuls und von der Stärke der von der Flüssigkeit in den Gefässboden eintretenden Impulsstrom, der Bodendruckkraft.
+Hat das Gefäss die Form einer Schraubenfeder, besteht kein direkter Zusammenhang mehr zwischen gravitativ zugeführtem Impuls (Gewichtskraft) und Impulsstromstärke bei der Grenzfläche zwischen der Flüssigkeit und dem Gefässboden (Bodendruckkraft). Bei dermassen verdrehten Gefässen fliesst der gravitativ zugeführte ''z''-Impuls auf seinem Weg nach unten abwechselnd durch die Flüssigkeit und die Gefässwände.
 [[Kategorie:Hydro]] [[Kategorie:OffSys]]