Lösung zu Bowling: Unterschied zwischen den Versionen

Inhalt hinzugefügt Inhalt gelöscht

Inline

Aktuelle Version vom 9. Mai 2012, 08:13 Uhr

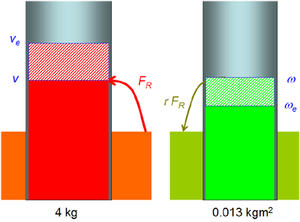
Die Umfangsgeschwindigkeit der Bowlingkugel bezüglich ihrer Mitte beträgt [math]v_U = \omega r[/math] = 75 rad/s * 0.09 m = 6.75 m/s. Die Kugel dreht sich somit schneller, als wenn sie nur abrollen würde. Folglich reduziert die Gleitreibungskraft die Winkelgeschwindigkeit und wirkt in Bewegungsrichtung.

Die Gleitreibung führt der Kugel Impuls zu. Dieser Impuls fliesst in der Kugel quer zu seiner Bezugsrichtung. Längs des quer fliessenden Impulses bildet sich eine Drehimpulssenke.
Der in der Kugel von der Berührfläche zur Mitte quer fliessende Impuls erzeugt eine Drehimpulssenke der Stärke Reibkraft mal Radius: [math]\Sigma_L =M= F_R \cdot r [/math] (Hebelgesetz).
In der Rollphase muss die Umfangsgeschwindigkeit der Kugel bezüglich ihrer Mitte gleich der Geschwindigkeit dieser Mitte sein: [math]v_{MMP} = \omega \cdot r[/math].
Die Änderungsraten von Drehimpuls und Impuls sind über das Hebelgesetz fest verkuppelt. Folglich ist auch die Änderung des Drehimpulses fest mit der Änderung des Impulses verknüpft. Hier nimmt in der Rutschphase der Impuls zu und der Drehimpuls ab: [math]r = \frac {F_R r}{F_R} = \frac {- \Delta L}{\Delta p} = \frac {J(\omega_a - \omega_e)}{m(v_e - v_a)}= \frac {J(\omega_a - v_e/r)}{m(v_e - v_a)}[/math]. Löst man diese Gleichung nach der Endgeschwindigkeit auf, erhält man [math]v_e = \frac {rmv_a + J\omega_a}{rm + J/r}[/math] = (0.09 m * 4 kg * 3 m/s + 0.013 kgm² * 75 rad/s) / (0.09 m * 4 kg + 0.013 kgm² / 0.09 m) = 4.07 m/s. Die Kugel dreht sich dann mit einer Winkelgeschwindigkeit von 4.07 m/s / 0.09 m = 45.2 rad/s.
Impuls wird von der Erde in die Kugel gepumpt, Drehimpuls fliesst weg. Die dabei umgesetzte Energie ist gleich Menge mal mittlere Pump- bzw. Fallhöhe. Die Energie für das Hochpumpen des Impulses stammt aus der freigesetzen Energie des fallenden Drehimpulses. Der Rest wird dissipiert: [math]W_{diss} = \Delta p \overline v - \Delta L \overline \omega[/math]. Während der Rutschphase beträgt der übertragene Impuls 4 kg * (4.07 m/s - 3 m/s) = 4.28 Ns, die mittlere Geschwindigkeitsdifferenz zwischen Kugel und Bahn (3 m/s + 4.07 m/s) / 2 = 3.54 m/s, der übertragene Drehimpuls 0.013 kgm² * (45.2 rad/s - 75 rad/s) = - 0.387 Nms und die mittlere Winkelgeschwindigkeitsdifferenz (75 rad/s + 45.2 rad/s) / 2 = 60.1 rad/s. Die Impuls-Pumparbeit beträgt 4.28 Ns * 3.54 m/s = 15.2 J, der wegströmende Drehimpuls setzt 0.387 Nms * 60.1 rad/s = 23.3 J Energie frei, folglich werden 23.3 J - 15.2 J = 8.1 J Energie zwischen Kugel und Bahn dissipiert.

Mehr zu diesem Thema unter Kegeln.

Aufgabe

@@ Zeile 1: / Zeile 1: @@
 [[Bild:Bowling_FB.png|thumb|Flüssigkeitsbild]] Die Umfangsgeschwindigkeit der Bowlingkugel bezüglich ihrer Mitte beträgt <math>v_U = \omega r</math> = 75 rad/s * 0.09 m = 6.75 m/s. Die Kugel dreht sich somit schneller, als wenn sie nur abrollen würde. Folglich reduziert die [[Gleitreibung]]skraft die Winkelgeschwindigkeit und wirkt in Bewegungsrichtung.
 #Die Gleitreibung führt der Kugel [[Impuls]] zu. Dieser Impuls fliesst in der Kugel quer zu seiner Bezugsrichtung. Längs des quer fliessenden Impulses bildet sich eine Drehimpulssenke.
-#Der in der Kugel von der Berührfläche zur Mitte quer fliessende Impuls erzeugt eine Drehimpulssenke der Stärke ''Reibkraft mal Radius'': <math>\Pi_L = F_R \cdot r </math> ([[Hebelgesetz]]).
+#Der in der Kugel von der Berührfläche zur Mitte quer fliessende Impuls erzeugt eine Drehimpulssenke der Stärke ''Reibkraft mal Radius'': <math>\Sigma_L =M= F_R \cdot r </math> ([[Hebelgesetz]]).
 #In der Rollphase muss die Umfangsgeschwindigkeit der Kugel bezüglich ihrer Mitte gleich der Geschwindigkeit dieser Mitte sein: <math>v_{MMP} = \omega \cdot r</math>.
-#Die Änderungsraten von [[Drehimpuls]] und [[Impuls]] sind über das Hebelgesetz fest verkuppelt. Folglich ist auch die Änderung des Drehimpulses fest mit der Änderung des Impulses verknüpft. Hier nimmt in der Rutschphase der Impuls zu und der Drehimpuls ab: <math>r = \frac {F_R r}{F_R} = \frac {- \Delta L}{\Delta p} = \frac {J(\omega_a - \omega_e)}{m(v_e - v_a)}= \frac {J(\omega_a - v_e/r)}{m(v_e - v_a)}</math>. Löst man diese Gleichung nach der Endgeschwindigkeit auf, erhält man <math>v_e = \frac {rmv_a + J\omega_a}{rm + J/r}</math> = (0.09 m * 4 kg * 3 m/s + 0.013 kgm<sup>2</sup> * 75 rad/s) / (0.09 m * 4 kg + 0.013 kgm<sup>2</sup> / 0.09 m) = 4.07 m/s. Die Kugel dreht sich dann mit einer Winkelgeschwindigkeit von 45 s<sup>-1</sup>.
+#Die Änderungsraten von [[Drehimpuls]] und [[Impuls]] sind über das Hebelgesetz fest verkuppelt. Folglich ist auch die Änderung des Drehimpulses fest mit der Änderung des Impulses verknüpft. Hier nimmt in der Rutschphase der Impuls zu und der Drehimpuls ab: <math>r = \frac {F_R r}{F_R} = \frac {- \Delta L}{\Delta p} = \frac {J(\omega_a - \omega_e)}{m(v_e - v_a)}= \frac {J(\omega_a - v_e/r)}{m(v_e - v_a)}</math>. Löst man diese Gleichung nach der Endgeschwindigkeit auf, erhält man <math>v_e = \frac {rmv_a + J\omega_a}{rm + J/r}</math> = (0.09 m * 4 kg * 3 m/s + 0.013 kgm<sup>2</sup> * 75 rad/s) / (0.09 m * 4 kg + 0.013 kgm<sup>2</sup> / 0.09 m) = 4.07 m/s. Die Kugel dreht sich dann mit einer Winkelgeschwindigkeit von 4.07 m/s / 0.09 m = 45.2 rad/s.
-#Impuls wird von der Erde in die Kugel gepumpt, Drehimpuls fliesst weg. Die dabei umgesetzte Energie ist gleich Menge mal mittlere Pump- bzw. Fallhöhe <math>W_{diss} = \Delta p \overline v - \Delta L \overline \omega</math>. Während der Rutschphase werden 4.3 Ns Impuls im Mittel um 3.5 m/s hinauf gepumpt. Die dazu notwendige Energie stammt vom Drehimpuls (0.39 Nms), der im Mittel um 60 s<sup>-1</sup> hinunterfällt. Die Impuls-Pumparbeit beträgt 15.2 J, der wegströmende Drehimpuls setzt 23.2 J Energie frei, folglich werden 8 J Energie zwischen Kugel und Bahn dissipiert.
+#Impuls wird von der Erde in die Kugel gepumpt, Drehimpuls fliesst weg. Die dabei umgesetzte Energie ist gleich Menge mal mittlere Pump- bzw. Fallhöhe. Die Energie für das Hochpumpen des Impulses stammt aus der freigesetzen Energie des fallenden Drehimpulses. Der Rest wird dissipiert: <math>W_{diss} = \Delta p \overline v - \Delta L \overline \omega</math>. Während der Rutschphase beträgt der übertragene Impuls 4 kg * (4.07 m/s - 3 m/s) = 4.28 Ns, die mittlere Geschwindigkeitsdifferenz zwischen Kugel und Bahn (3 m/s + 4.07 m/s) / 2 = 3.54 m/s, der übertragene Drehimpuls 0.013 kgm<sup>2</sup> * (45.2 rad/s - 75 rad/s) = - 0.387 Nms und die mittlere Winkelgeschwindigkeitsdifferenz (75 rad/s + 45.2 rad/s) / 2 = 60.1 rad/s. Die Impuls-Pumparbeit beträgt 4.28 Ns * 3.54 m/s = 15.2 J, der wegströmende Drehimpuls setzt 0.387 Nms * 60.1 rad/s = 23.3 J Energie frei, folglich werden 23.3 J - 15.2 J = 8.1 J Energie zwischen Kugel und Bahn dissipiert.
 Mehr zu diesem Thema unter [[Kegeln]].
-'''[[Bowling]]'''
+'''[[Bowling|Aufgabe]]'''