Hebelgesetz
Phänomen
Archimedes gilt als Entdecker des Hebelgesetzes. Archimedes zeigte, wie ein in einem Drehpunkt verankerter Hebel eine schwere "Last" mit einer verhältnismäßig geringen "Kraft" heben kann.
Der Hebel gehört zu den einfachen Maschinen. Man unterscheidet zwischen ein- und zweiarmigen Hebeln. Beim einarmigen Hebel wirken "Last" und "Kraft" auf der gleichen Seite der Verankerung, beim zweiarmigen greifen die beiden Wirkungen auf verschiedenen Seiten an. Der Hebel hat viele Anwendungsmöglichkeiten:
- einarmig: Flaschenöffner, Nussknacker
- zweiarmig: Apothekerwaage, Turmkran (Baukran)
- komplexer: Gemüsewaage, Dezimalwaage
elementare Formulierung
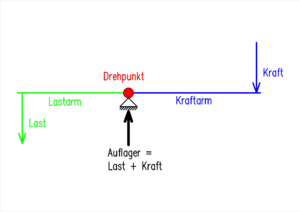
In der Physik wird das Drehmoment oft über das Hebelgesetz eingeführt. Dabei schreibt man den am Hebel angreifenden Kräften eine Wirklinie zu. Die Wirklinie geht durch den "Angriffspunkt" der Kraft und verläuft parallel zur Richtung des Kraftvektors. Dann definiert man das Drehmoment als
Kraft mal Abstand der Wirklinie zur Drehachse,
wobei man zwischen linksdrehenden (gegen den Uhrzeigersinn) und rechstdrehenden (mit den Zeigern der Uhr) unterscheidet. Diese Definition des Drehmomentes ist korrekt, solange der Hebel um die Drehachse frei drehbar gelagert ist, solange der Hebel längs dieser Achse beliebig Impuls mit der Erde austauschen kann.
Das Hebelgesetz besagt dann, dass ein Hebel im Gleichgewicht ist, wenn die Summe der linksdrehenden Drehmomente mit der Summe der rechtsdrehenden Drehmomente übereinstimmt.
Statik
In der Statik, einem Teilgebiet der technischen Mechanik, wird von jedem Teilkörper ein Schnittbild erstellt. Nun wählt man einen beliebigen Punkt aus (frei gewählter Bezugspunkt oder Ursprung des Koordinatensystems) und definiert das statische Drehmoment als
- [math]\vec M=\vec r\times\vec F[/math]
Der Distanzvektor r zeigt vom Bezugspunkt bis zum Mittelpunkt der Kraftangriffsfläche, dem Angriffspunkt der Kraft. Bei der Gewichts- oder Schwerkraft darf der Schwerpunkt als Angriffspunkt genommen werden. Oft wird der Distanzvektor r von Angriffspunkt zum Bezugspunkt hin orientiert. Dann müssen Kraft und Distanzvektor im Kreuzprodukt der Definitionsgleichung vertauscht werden. Setzt man den Bezugspunkt in den Ursprung des Koordinatensystems, ist der Distanzvektor gleich dem Ortsvektor des Angriffspunktes.
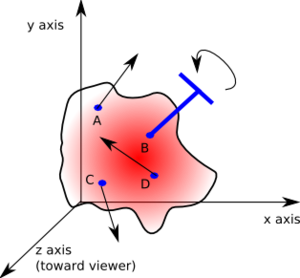
In der Komponentendarstellung lautet die Definition des Drehmomentes
- [math]\begin{pmatrix}M_x\\M_y\\M_z\end{pmatrix}=\begin{pmatrix}yF_z &- &zF_y\\zF_x &- &xF_z\\xF_y &- &yF_x \end{pmatrix}[/math]
wobei der Vektor r = (x, y, z) vom Bezugspunkt oder vom Ursprung des Koordinatensystems aus gemessen wird.
Mit dieser Definition wird das Hebelgesetz Teil der allgemeinen Gleichgewichtsbedingung der Statik (die Gleichgewichtsbedingung bezüglich der Rotation ist einen Spezialfall der Drehimpulsbilanz)
- [math]\sum_{i}\vec M_i+\sum_{j}(\vec r_j \times \vec F_j) = 0[/math]
Die erste Summe beschreibt die reinen Drehmomente (Stärken der Drehimpulsströme) bezüglich des Systems, der zweite Summe umfasst die Drehmomente, die über das Hebelgesetz den Kräften zugeordet werden können (Stärken der Drehimpulsquellen).
Drehimpulsquelle
Die Physik der dynamischen Systeme liefert eine konsistente Erklärung zum Hebelgesetz
Fliesst in einem Bauteil ein Impulsstrom quer zu seiner eigenen Bezugsrichtung, bildet sich eine Drehimpulsquelle bezüglich dieses Bauteils.
Die Stärke der Drehimpulsquelle ergibt sich direkt aus dem Hebelgesetz
- [math]\begin{pmatrix} \Sigma_{Lx}\\ \Sigma_{Ly} \\ \Sigma_{Lz}\end{pmatrix}=\begin{pmatrix} \Delta z I_{py} - \Delta y I_{pz}\\ \Delta x I_{pz} - \Delta z I_{px} \\ \Delta y I_{px} - \Delta x I_{py}\end{pmatrix}[/math]
wobei Δr (Δx, Δy, Δz) die Strecke darstellt, um die der Impuls im Mittel seitwärts fliesst.
Diese definierende Erklärung des Hebelgesetzes als Drehimpulsquelle reicht über die Statik hinaus. Die Drehimpulsquellen bilden einen Teil der Drehimpulsbilanz bezüglich eines festen Körpers.
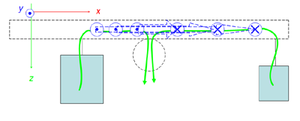
Nimmt man den zweiarmigen Hebel und führt ein geeignet gewähltes Koordinatensystem ein, beschreiben sowohl die "Last" als auch die "Kraft" eine Impulsstromstärke bezüglich des Systems Hebel. Beide Impulsströme fliessen im Hebel vom Angriffspunkt zur Drehachse oder umgekehrt und bilden dabei je eine linienflüchtige Drehimpulsquelle, wobei die Quellenstärke längs des einen Stromes positiv und längs des andern negativ ist. Der Drehimpuls muss dann im Innern des Hebels von den Quellen zu den Senken (negative Quelle) fliessen. Die Drehimpulsstromstärke bezüglich des Hebelquerschnitts heisst in der Statik Biegemoment. Weil Drehimpulsströme immer von Impulsströmen begrenzt sein müssen, bricht der Hebel an der Stelle mit der stärksten Drehimpulsstromstärke, also in der Regel bei der Verankerung.
Energiebetrachtung
Ein idealer Hebel erzeugt weder Energie noch vernichtet er welche. Dies lässst sich mit Hilfe der Arbeit bei einer infinitesimalen Drehung des Hebels zeigen. Dabei vergleicht man die Arbeit der "Last" mit der der "Kraft" bei einer Drehung des Hebels und den Winkel δφ
- [math]\delta W(F_L)=F_L s_L\delta\varphi=F_K s_K\delta\varphi=\delta W(F_K)[/math]
Die Physik der dynamischen Systeme liefert dazu eine prozessmässige Erklärung: Die von den Impulsströmen im Bauteil umgesetzen Prozessleistungen entsprechen gerade den Energieströmen, die den über die zugehörigen Quellen zu- oder abfliessenden Drehimpulsströmen zuzuordnen sind
- [math]P =I_{pz}\Delta v_z=I_{pz} \omega_y \Delta x=\Sigma_{Ly}\omega_y=I_W(I_{Ly})[/math]
Bei der Formulierung dieser Gleichung ist angenommen worden, dass der Hebel parallel zur x-Richtung ausgerichtet ist und die Kräfte nach unten, also in z-Richtung zeigen. Diese Energiebetrachtung, wonach die Leistung eines Impulsstromes dem zugeordneten Energiestrom des durch die Quelle ausgetauschten Drehimpulses entspricht, kann verallgemeinert und von der Komponentendarstellung gelöst werden
- [math]P=I_{\vec p}\bullet\Delta \vec v=I_{\vec p}\bullet(\vec\omega\times\Delta\vec r)=\Sigma_{\vec L} \bullet\vec\omega=I_W[/math]
Video
- <videoflash>jgJqN8tePnU|640|360</videoflash>