Kegeln: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
(→Links) |
||
| (13 dazwischenliegende Versionen von einem anderen Benutzer werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
==Theorie== |
==Theorie== |
||
[[Bild:KegelnStrombild.jpg|thumb|Impuls- und Drehimpulsströme bezüglich der Kugel]] |
[[Bild:KegelnStrombild.jpg|thumb|Impuls- und Drehimpulsströme bezüglich der Kugel]] |
||
Mit der Einführung eines globalen Koordinatensystems zerlegen wir die "Bewegungsmenge" in die drei Sorten ''x''-[[Impuls]] (Bewegungsrichtung), ''y''-Impuls (vertikal) und ''z''-[[Drehimpuls]] (normal zur |
Mit der Einführung eines globalen Koordinatensystems zerlegen wir die "Bewegungsmenge" in die drei Sorten ''x''-[[Impuls]] (Bewegungsrichtung), ''y''-Impuls (vertikal) und ''z''-[[Drehimpuls]] (normal zur Rotationsebene). Sobald die Kugel abgesetzt ist, wird der gravitativ in den Körper hineinquellende ''y''-Impuls unmittelbar an die Unterlage abgeführt. Der zugehörige [[Impulsstrom]] belastet die Kugel auf [[Druck]] (nach unten zunehmend). Der ''x''-Impuls fliesst anfänglich mit grosser Stärke (Rutschphase) und später nur noch im geringen Masse (Rollphase) aus der Kugel nach unten an die Unterlage weg. Dieser quer zur eigenen Bezugsrichtung fliessende ''x''-Impulsstrom erzeugt eine ''z''-[[Quelle|Drehimpulsquelle]]. Ein Teil des über die Quelle zugeführten ''z''-Drehimpulses fliesst reibungsbedingt ebenfalls an die Unterlage weg. |
||
[[Bild:KegelnSchnittbild.jpg|thumb|Kräfte und Drehmomente auf die Kugel]] |
[[Bild:KegelnSchnittbild.jpg|thumb|Kräfte und Drehmomente auf die Kugel]] |
||
Im [[Schnittbild]] ordnet man der Stärke des volumenmässig vom [[Gravitationsfeld]] her |
Im [[Freischneiden|Schnittbild]] ordnet man der Stärke des volumenmässig vom [[Gravitationsfeld]] her zufliessenden Impulses einen Pfeil zu, der nach unten zeigt, die Stärke ''m '''g''''' hat und Gewichtskraft heisst. Die Stärke des Impulsstromes bezüglich eines Oberflächenstückes nennt man Schnitt- oder Oberflächenkraft. Die Stärke des Drehimpulsstromes heisst [[Drehmoment]]. Ein im Körper seitwärts fliessender Impulsstrom bildet eine Drehimpulsquelle ([[Hebelgesetz]]). |
||
Im Schnittbild der Kugel zeigt das Gewicht ('''''F'''<sub>G</sub>'') die Stärke des Zuflusses von ''y''-Impuls und die Normalkraft ('''''F'''<sub>N</sub>'') die des Abflusses an. Die Reibkraft ('''''F'''<sub>R</sub>'') steht für die Stärke des abliessenden ''x''-Impulsstromes. Das Reibdrehmoment ('''''M'''<sub>R</sub>'') beschreibt die Stärke des abfliessenden ''z''-Drehimpulses. Die Drehimpulsquelle wird im Schnittbild nicht eingezeichnet, muss aber bei der Formulierung der Bilanzgleichungen (Grundgesetze) über das korrekt formulierte [[Hebelgesetz]] berücksichtigt werden. |
Im Schnittbild der Kugel zeigt das Gewicht ('''''F'''<sub>G</sub>'') die Stärke des Zuflusses von ''y''-Impuls und die Normalkraft ('''''F'''<sub>N</sub>'') die des Abflusses an. Die Reibkraft ('''''F'''<sub>R</sub>'') steht für die Stärke des abliessenden ''x''-Impulsstromes. Das Reibdrehmoment ('''''M'''<sub>R</sub>'') beschreibt die Stärke des abfliessenden ''z''-Drehimpulses. Die Drehimpulsquelle wird im Schnittbild nicht eingezeichnet, muss aber bei der Formulierung der Bilanzgleichungen (Grundgesetze) über das korrekt formulierte [[Hebelgesetz]] berücksichtigt werden. |
||
| Zeile 21: | Zeile 21: | ||
<math>{-}r = \frac {\Sigma_{Lz}}{I_{px}} = \frac {\Delta L_z}{\Delta p_x} = \frac {J(\omega_{ze}-0)}{m(v_{xe}-v_{xa})} = \frac {J(v_{xe}/r-0)}{m(v_{xe}-v_{xa})}</math> |
<math>{-}r = \frac {\Sigma_{Lz}}{I_{px}} = \frac {\Delta L_z}{\Delta p_x} = \frac {J(\omega_{ze}-0)}{m(v_{xe}-v_{xa})} = \frac {J(v_{xe}/r-0)}{m(v_{xe}-v_{xa})}</math> |
||
(Erklärung zum zweiten Gleichheitszeichen: weil die ''z''-Drehimpulsquelle ''Σ<sub>Lz</sub>'' über das Hebelgesetz mit dem Impulsstrom verknüpft ist, muss auch die Drehimpulsänderung gleich minus Radius mal Impulsänderung sein.) Durch Auflösen nach der Endgeschwindigkeit erhält man |
|||
<math>v_{xe} = \frac {m}{m + J/r^2} \cdot v_{xa}</math> |
<math>v_{xe} = \frac {m}{m + J/r^2} \cdot v_{xa}</math> |
||
| Zeile 32: | Zeile 32: | ||
<math>W_{rot} = \overline{\omega_z} L_z = \frac {1}{2} J \omega_z^2</math> |
<math>W_{rot} = \overline{\omega_z} L_z = \frac {1}{2} J \omega_z^2</math> |
||
Der nach unten wegfliessende ''x''-Impuls verliert - je nach Drehzahl der Kugel - schon im Innern der Kugel an Potenzial. |
Der nach unten wegfliessende ''x''-Impuls verliert - je nach Drehzahl der Kugel - schon im Innern der Kugel an Potenzial (Geschwindigkeit). Folglich setzt der ''x''-Impulsstrom schon im Innern der Kugel Energie frei. Diese Prozessleistung dient dazu, den Drehimpuls auf die entsprechende "Höhe" zu befördern |
||
<math>P = \Delta v_x I_{px} = \omega_z r I_{px} = \omega_z \Sigma_{Lz} = I_W</math> |
<math>P = \Delta v_x I_{px} = \omega_z r I_{px} = \omega_z \Sigma_{Lz} = I_W</math> |
||
| Zeile 40: | Zeile 40: | ||
<math>P_{diss} = (v_x - \omega r) I_{px}</math> |
<math>P_{diss} = (v_x - \omega r) I_{px}</math> |
||
Die Energiedissipation der Rollreibung hängt |
Die Energiedissipation der Rollreibung hängt in unserem Modell nicht davon ab, ob der Körper rollt oder rutscht |
||
<math>P_{diss} = \omega_z I_{Lz}</math> |
<math>P_{diss} = \omega_z I_{Lz}</math> |
||
| Zeile 48: | Zeile 48: | ||
Das nebenstehend abgebildete [[Systemdiagramm]] zeigt das Modell der Kugel. Auf der untersten Zeile sind die Parameter und die Anfangswerte aufgeführt. Im Gegensatz zur Gleitreibungskraft (''Reibkraft''), die mit der Masse verknüpft ist, wird das Reibdrehmoment direkt parametrisiert. Man könnte das Reibdrehmoment auch von der Masse, dem Radius und einem weiteren Faktor abhängig machen. |
Das nebenstehend abgebildete [[Systemdiagramm]] zeigt das Modell der Kugel. Auf der untersten Zeile sind die Parameter und die Anfangswerte aufgeführt. Im Gegensatz zur Gleitreibungskraft (''Reibkraft''), die mit der Masse verknüpft ist, wird das Reibdrehmoment direkt parametrisiert. Man könnte das Reibdrehmoment auch von der Masse, dem Radius und einem weiteren Faktor abhängig machen. |
||
Über der |
Über der Zeile mit den Parametern und Anfangswerten ist die Bilanz für den ''x''-Impuls und den ''z''-Drehimpuls formuliert. Die Kopplung zwischen dem nach unten wegfliessenden Impulsstrom und der Drehimpulsquelle ist mit einem Wirkungspfeil (arrow) gekennzeichnet. Der Quotient aus Impulsinhalt und Masse ergibt die momentane Geschwindigkeit des Massenmittelpunktes. Entsprechend erhält man die Winkelgeschwindigkeit aus Drehimpuls und Massenträgheitsmoment. Um den reibungsbedingten Impuls- bzw. Drehimpulsstrom zu berechnen, wird für die Schlupfgeschwindigkeit (''v unten'') und die Winkelgeschwindigkeit je eine Vorzeichenfunktion (''sgn v unten'' und ''sgn w'') gebildet. Solange man mit festen Schrittweiten und guter zeitlicher Auflösung rechnet, eignet sich die auf eins normierte und mit einem Faktor vor dem Argument gestauchte '''Arcustangens'''-Funktion gut, um die Vorzeichenfunktion nachzubilden. |
||
Die Dynamik |
Die Dynamik wirkt auf der Ebene Impuls, Drehimpuls, Geschwindigkeit und Winkelgeschwindigkeit. Will man die Strecke oder den Drehwinkel berechnen, muss über die Geschwindigkeit oder über die Winkelgeschwindigkeit aufzusummiert werden. Dies geschieht hier für die von der Kugel zurückgelegten Strecke mit einer Rohr-Topf-Anordnung (zweite Ebene). |
||
Die Energie bildet neben der Bilanz- und der Geometrieebene die dritte Etage. |
Die Energie bildet neben der Bilanz- und der Geometrieebene die dritte Etage. Im hier abgebildeten SD-Modell werden die Prozessleistungen für die beiden Reibungseffekte berechnet (Stromstärke mal Potenzialdifferenz) und mit einer Rohr-Topf-Anordnung aufintegriert. |
||
==Simulation== |
==Simulation== |
||
[[Bild:KegelnDiagramm.gif|thumb|''v-t-'' und ''ω-t-''Diagramm]] |
|||
Mit den '''Anfangsbedingungen''' Geschwindigkeit 8 m/s, keine Winkelgeschwindigkeit und der gewählten '''Parametrisierung''' (Masse 2.8 kg, Radius 0.08 m, Gleitreibungszahl 0.5, Rolreibungsmoment 0.08 Nm) dauert es etwa eine halbe Sekunde bis die Kugel ins Rollen kommt. Unter Vernachlässigung des Rollreibungsdrehmoments erhält man für eine Kugel (''J'' = ''0.4 m r<sup>2</sup>'') gemäss der oben aufgeführten Formel eine Endgeschwindigkeit von 5.7 m/s. Die Rollreibung setzt diesen Wert nur ganz wenig hinunter. In der Rollphase nehmen Geschwindigkeit und Winkelgeschwindigkeit linear mit der Zeit ab. |
|||
[[Bild:KegelnDiagramm2.gif|thumb|''I<sub>px</sub>-t'' und ''I<sub>Lz</sub>-t-''Diagramme]] |
|||
Die Stärken des ''x''-Impulsstromes und der damit verknüpften ''z''-Drehimpulsquelle sind anfänglich sehr gross. Sobald die Rollbewegung einsetzt, erzwingt das Rolldrehmoment einen dissipationsfreien Impulsabfluss. Die vom Impulsstrom freigesetzte Energie wird vollständig zum "Pumpen" des Drehimpulses (Quelle) benötigt. Dissipiert wird die Energie also nur durch den Abfluss von Drehimpuls. Nur der Drehimpuls "fällt" an der Kugeloberfläche über eine Potenzialdifferenz, über eine sprunghafte Änderung der Winkelgeschwindigkeit. Der abfliessende Impuls verlässt die Kugel in der Rollphase dagegen auf "Nullniveau". |
|||
Will man also das Phänomen Rollreibung im Schnittbild erklären, muss ein Rollreibdrehmoment und eine Haftreibungskraft eingezeichnet werden. Die Haftreibungskraft steht für den Impulsabfluss, das Rolldrehmoment für den Drehimpulsabfluss. Das Hebelgesetz sorgt dann dafür, dass die vom Impulsstrom im Innern der Kugel freigesetzte Energe zu jedem Zeitpunkt genau so gross ist wie die Energie, die vom zufliessenden Drehimpuls benötigt wird. Diese Kopplung zwischen abfliessendem Impuls und zugeführtem Drehimpuls bezeichnet man etwas salop als Umwandlung von kinetischer Energie in Rotationsenergie. |
|||
==Modelica== |
|||
[[Bild:Kegeln_Sim.png|thumb|Impulsstromstärke (Reibungskraft) bezüglich Kugel]] |
|||
Mit der [[Modelica]]-Bibliothek [[SystemPhysik]] lässt sich dieses Problem in kürzester Zeit modellieren. Als Basis wird das Element ''Rolle'' der Bibliothek entnommen und parametrisiert. Den Drehimpulsanschluss der ''Rolle'' verbindet man über das Element ''Drehreibung'' mit der ''Erde''. Einen der beiden seitlichen Impulsanschlüsse der ''Rolle'' verknüpft man analog dazu über das Element ''Reibung'' mit der ''Erde''. Der Sensor ''Strecke'' liefert den von der Kugel zurückgelegten Weg. |
|||
Das Diagramm zeigt den Kraft-Zeit-Verlauf der Reibungskraft. In der ersten Phase wirkt eine Gleitreibung, die kurz bevor die Kugel rollt auf den maximalen Haftreibunswert (Stribeck-Effekt) ansteigt. Danach fliesst gerade noch so viel Impuls an die Erde weg, damit die Rollbedingung erfüllt bleibt. Die Haftreibungskraft ist ohne Dissipation und der Begriff Rollreibungskraft demnach ein Ammenmärchen. Die Sache ist um einiges komplexer: bei der Rollreibung fliesst primär Drehimpuls an die Unterlage weg; damit die Rollbedingung erfüllt bleibt, muss auch Impuls abfliessen; der zugehörige Impulsstrom wirkt als Drehimpulsquelle. Demnach fliesst mehr Drehimpuls an die Unterlage weg, als die Kugel an Inhalt verliert. Obwohl kinetische und Rotationsenergie gemeinsam abnehmen, wird die Energie nur vom Drehimpulsstrom dissipiert. |
|||
==Links== |
|||
*[https://www.youtube.com/watch?v=6DyI4h_tnvI Bowling] auf Youtube |
|||
[[Kategorie:Trans]] [[Kategorie:Rot]] [[Kategorie: Modelle]] [[Kategorie: TransMod]] [[Kategorie: RotMod]] |
[[Kategorie:Trans]] [[Kategorie:Rot]] [[Kategorie: Modelle]] [[Kategorie: TransMod]] [[Kategorie: RotMod]] |
||
Aktuelle Version vom 29. Juni 2014, 13:36 Uhr
Phänomen
Kegeln ist eine Sportart, bei der eine Kugel auf einer glatten Bahn gegen neun Kegel geschossen wird. Neben den drei europäischen Varianten (Asphaltbahn, Bohlenbahn und Scherenbahn) kennt man noch das amerikanische Bowling. Beim Kegeln wird die Kugel auf der Auflagebohle abgesetzt. Nach einer anfänglichen Rutschpartie geht die Kugel in ein sich verlangsamendes Rollen über.
Wir betrachten hier nur die Bewegung längs einer Geraden. Verwandte Phänome findet man beim rotierend weggeworfenen Gymnastikring (Hulahup) oder bei einem rotierend abgesetzten Kugellager (beliebtes, aber gefährliches Spiel von Lehrlingen der Maschinenbaubranche).
Theorie
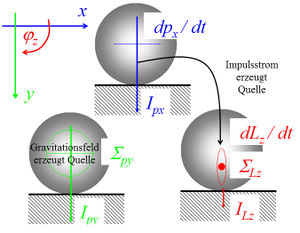
Mit der Einführung eines globalen Koordinatensystems zerlegen wir die "Bewegungsmenge" in die drei Sorten x-Impuls (Bewegungsrichtung), y-Impuls (vertikal) und z-Drehimpuls (normal zur Rotationsebene). Sobald die Kugel abgesetzt ist, wird der gravitativ in den Körper hineinquellende y-Impuls unmittelbar an die Unterlage abgeführt. Der zugehörige Impulsstrom belastet die Kugel auf Druck (nach unten zunehmend). Der x-Impuls fliesst anfänglich mit grosser Stärke (Rutschphase) und später nur noch im geringen Masse (Rollphase) aus der Kugel nach unten an die Unterlage weg. Dieser quer zur eigenen Bezugsrichtung fliessende x-Impulsstrom erzeugt eine z-Drehimpulsquelle. Ein Teil des über die Quelle zugeführten z-Drehimpulses fliesst reibungsbedingt ebenfalls an die Unterlage weg.
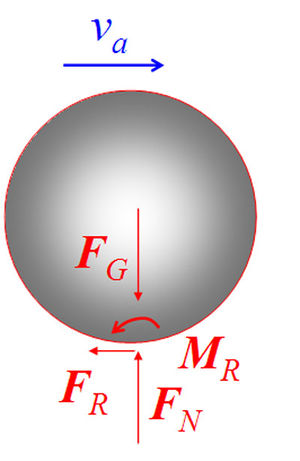
Im Schnittbild ordnet man der Stärke des volumenmässig vom Gravitationsfeld her zufliessenden Impulses einen Pfeil zu, der nach unten zeigt, die Stärke m g hat und Gewichtskraft heisst. Die Stärke des Impulsstromes bezüglich eines Oberflächenstückes nennt man Schnitt- oder Oberflächenkraft. Die Stärke des Drehimpulsstromes heisst Drehmoment. Ein im Körper seitwärts fliessender Impulsstrom bildet eine Drehimpulsquelle (Hebelgesetz).
Im Schnittbild der Kugel zeigt das Gewicht (FG) die Stärke des Zuflusses von y-Impuls und die Normalkraft (FN) die des Abflusses an. Die Reibkraft (FR) steht für die Stärke des abliessenden x-Impulsstromes. Das Reibdrehmoment (MR) beschreibt die Stärke des abfliessenden z-Drehimpulses. Die Drehimpulsquelle wird im Schnittbild nicht eingezeichnet, muss aber bei der Formulierung der Bilanzgleichungen (Grundgesetze) über das korrekt formulierte Hebelgesetz berücksichtigt werden.
Die Stromdarstellung mag komplizierter erscheinen als der Zugang über das Schnittbild. Wenn man aber bedenkt, dass in den meisten deutschsprachigen Lehrbüchern zur Physik nicht zwischen Gewichts- und Normalkraft unterschieden wird, die Dissipation beim Rollen mit einer unsinnigen Rollreibungskraft erklärt wird und das Hebelgesetz auf die Drehachse statt auf den Massenmittelpunkt bezogen wird, sollte man ernsthaft über eine Neudarstellung der Mechanik nachdenken. Die Physik der dynamischen Systeme hat zwar noch nicht den für den Unterricht auf allen Stufen erforderlichen Reifegrad erreicht, führt aber immer zu einer korrekten Darstellung der Schnittbilder.
Flüssigkeitsbild
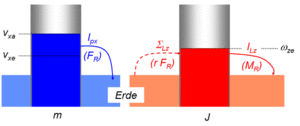
Im Flüssigkeitsbild erscheint der Impuls oder Drehimpuls als Flüssigkeit. Jeder Körper bildet ein Gefäss mit der Trägheit als Grundfläche und der zugehörigen Geschwindigkeit als Füllhöhe. Der nach unten, also quer zur Bezugsrichtung abfliessende x-Impulsstrom ist über die mittlere Länge des Impulstransportes (r) mit der z-Drehimpulsquelle geometrisch verknüpft. Lässt man den reibungsbedingten Drehimpulsabfluss ausser Acht, kann die Rollgeschwindigkeit der Kugel direkt aus dem Flüssigkeitsbild berechnet werden
[math]{-}r = \frac {\Sigma_{Lz}}{I_{px}} = \frac {\Delta L_z}{\Delta p_x} = \frac {J(\omega_{ze}-0)}{m(v_{xe}-v_{xa})} = \frac {J(v_{xe}/r-0)}{m(v_{xe}-v_{xa})}[/math]
(Erklärung zum zweiten Gleichheitszeichen: weil die z-Drehimpulsquelle ΣLz über das Hebelgesetz mit dem Impulsstrom verknüpft ist, muss auch die Drehimpulsänderung gleich minus Radius mal Impulsänderung sein.) Durch Auflösen nach der Endgeschwindigkeit erhält man
[math]v_{xe} = \frac {m}{m + J/r^2} \cdot v_{xa}[/math]
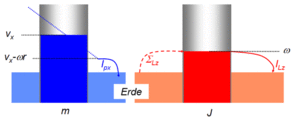
Das Flüssigkeitsbild liefert neben der anschaulichen Darstellung der Bilanz zusätzliche Informationen zur Energie. So ist die Prozessleistung gleich Stromstärke mal Fallhöhe oder die gespeicherte Bewegungsenergie gleich Impuls- bzw. Drehimpulsinhalt mal mittlere Pumphöhe
[math]W_{kin} = \overline{v_x} p_x = \frac {1}{2} m v_x^2[/math]
[math]W_{rot} = \overline{\omega_z} L_z = \frac {1}{2} J \omega_z^2[/math]
Der nach unten wegfliessende x-Impuls verliert - je nach Drehzahl der Kugel - schon im Innern der Kugel an Potenzial (Geschwindigkeit). Folglich setzt der x-Impulsstrom schon im Innern der Kugel Energie frei. Diese Prozessleistung dient dazu, den Drehimpuls auf die entsprechende "Höhe" zu befördern
[math]P = \Delta v_x I_{px} = \omega_z r I_{px} = \omega_z \Sigma_{Lz} = I_W[/math]
Während der Rutschphase dissipiert der abfliessende x-Impulsstrom Energie
[math]P_{diss} = (v_x - \omega r) I_{px}[/math]
Die Energiedissipation der Rollreibung hängt in unserem Modell nicht davon ab, ob der Körper rollt oder rutscht
[math]P_{diss} = \omega_z I_{Lz}[/math]
SD-Modell
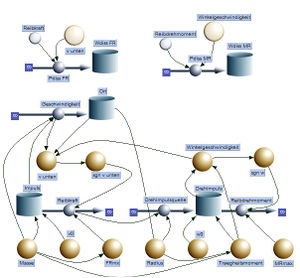
Das nebenstehend abgebildete Systemdiagramm zeigt das Modell der Kugel. Auf der untersten Zeile sind die Parameter und die Anfangswerte aufgeführt. Im Gegensatz zur Gleitreibungskraft (Reibkraft), die mit der Masse verknüpft ist, wird das Reibdrehmoment direkt parametrisiert. Man könnte das Reibdrehmoment auch von der Masse, dem Radius und einem weiteren Faktor abhängig machen.
Über der Zeile mit den Parametern und Anfangswerten ist die Bilanz für den x-Impuls und den z-Drehimpuls formuliert. Die Kopplung zwischen dem nach unten wegfliessenden Impulsstrom und der Drehimpulsquelle ist mit einem Wirkungspfeil (arrow) gekennzeichnet. Der Quotient aus Impulsinhalt und Masse ergibt die momentane Geschwindigkeit des Massenmittelpunktes. Entsprechend erhält man die Winkelgeschwindigkeit aus Drehimpuls und Massenträgheitsmoment. Um den reibungsbedingten Impuls- bzw. Drehimpulsstrom zu berechnen, wird für die Schlupfgeschwindigkeit (v unten) und die Winkelgeschwindigkeit je eine Vorzeichenfunktion (sgn v unten und sgn w) gebildet. Solange man mit festen Schrittweiten und guter zeitlicher Auflösung rechnet, eignet sich die auf eins normierte und mit einem Faktor vor dem Argument gestauchte Arcustangens-Funktion gut, um die Vorzeichenfunktion nachzubilden.
Die Dynamik wirkt auf der Ebene Impuls, Drehimpuls, Geschwindigkeit und Winkelgeschwindigkeit. Will man die Strecke oder den Drehwinkel berechnen, muss über die Geschwindigkeit oder über die Winkelgeschwindigkeit aufzusummiert werden. Dies geschieht hier für die von der Kugel zurückgelegten Strecke mit einer Rohr-Topf-Anordnung (zweite Ebene).
Die Energie bildet neben der Bilanz- und der Geometrieebene die dritte Etage. Im hier abgebildeten SD-Modell werden die Prozessleistungen für die beiden Reibungseffekte berechnet (Stromstärke mal Potenzialdifferenz) und mit einer Rohr-Topf-Anordnung aufintegriert.
Simulation
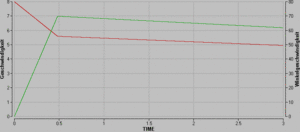
Mit den Anfangsbedingungen Geschwindigkeit 8 m/s, keine Winkelgeschwindigkeit und der gewählten Parametrisierung (Masse 2.8 kg, Radius 0.08 m, Gleitreibungszahl 0.5, Rolreibungsmoment 0.08 Nm) dauert es etwa eine halbe Sekunde bis die Kugel ins Rollen kommt. Unter Vernachlässigung des Rollreibungsdrehmoments erhält man für eine Kugel (J = 0.4 m r2) gemäss der oben aufgeführten Formel eine Endgeschwindigkeit von 5.7 m/s. Die Rollreibung setzt diesen Wert nur ganz wenig hinunter. In der Rollphase nehmen Geschwindigkeit und Winkelgeschwindigkeit linear mit der Zeit ab.
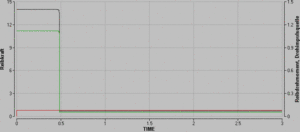
Die Stärken des x-Impulsstromes und der damit verknüpften z-Drehimpulsquelle sind anfänglich sehr gross. Sobald die Rollbewegung einsetzt, erzwingt das Rolldrehmoment einen dissipationsfreien Impulsabfluss. Die vom Impulsstrom freigesetzte Energie wird vollständig zum "Pumpen" des Drehimpulses (Quelle) benötigt. Dissipiert wird die Energie also nur durch den Abfluss von Drehimpuls. Nur der Drehimpuls "fällt" an der Kugeloberfläche über eine Potenzialdifferenz, über eine sprunghafte Änderung der Winkelgeschwindigkeit. Der abfliessende Impuls verlässt die Kugel in der Rollphase dagegen auf "Nullniveau".
Will man also das Phänomen Rollreibung im Schnittbild erklären, muss ein Rollreibdrehmoment und eine Haftreibungskraft eingezeichnet werden. Die Haftreibungskraft steht für den Impulsabfluss, das Rolldrehmoment für den Drehimpulsabfluss. Das Hebelgesetz sorgt dann dafür, dass die vom Impulsstrom im Innern der Kugel freigesetzte Energe zu jedem Zeitpunkt genau so gross ist wie die Energie, die vom zufliessenden Drehimpuls benötigt wird. Diese Kopplung zwischen abfliessendem Impuls und zugeführtem Drehimpuls bezeichnet man etwas salop als Umwandlung von kinetischer Energie in Rotationsenergie.
Modelica
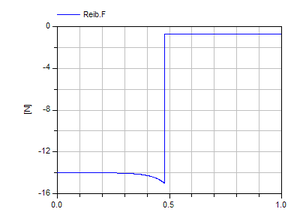
Mit der Modelica-Bibliothek SystemPhysik lässt sich dieses Problem in kürzester Zeit modellieren. Als Basis wird das Element Rolle der Bibliothek entnommen und parametrisiert. Den Drehimpulsanschluss der Rolle verbindet man über das Element Drehreibung mit der Erde. Einen der beiden seitlichen Impulsanschlüsse der Rolle verknüpft man analog dazu über das Element Reibung mit der Erde. Der Sensor Strecke liefert den von der Kugel zurückgelegten Weg.
Das Diagramm zeigt den Kraft-Zeit-Verlauf der Reibungskraft. In der ersten Phase wirkt eine Gleitreibung, die kurz bevor die Kugel rollt auf den maximalen Haftreibunswert (Stribeck-Effekt) ansteigt. Danach fliesst gerade noch so viel Impuls an die Erde weg, damit die Rollbedingung erfüllt bleibt. Die Haftreibungskraft ist ohne Dissipation und der Begriff Rollreibungskraft demnach ein Ammenmärchen. Die Sache ist um einiges komplexer: bei der Rollreibung fliesst primär Drehimpuls an die Unterlage weg; damit die Rollbedingung erfüllt bleibt, muss auch Impuls abfliessen; der zugehörige Impulsstrom wirkt als Drehimpulsquelle. Demnach fliesst mehr Drehimpuls an die Unterlage weg, als die Kugel an Inhalt verliert. Obwohl kinetische und Rotationsenergie gemeinsam abnehmen, wird die Energie nur vom Drehimpulsstrom dissipiert.
Links
- Bowling auf Youtube