Lösung zu RC-Glied mit zwei Kondensatoren: Unterschied zwischen den Versionen
Inhalt hinzugefügt Inhalt gelöscht
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| (4 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Bild:RCC-Glied_FB.png|thumb|Flüssigkeitsbild für die Kondensatoren]] |
|||
#Die Spannung über dem ersten Kondensator verkleinert sich um 11 V von 20 V auf 9 V. Die Spannung über dem zweiten Kondensator sinkt um 16.5 V von 7.5 V auf -9 V (bezogen auf die eingezeichneten Spannungspfeile). |
|||
Im [[Flüssigkeitsbild]] erscheint der erste Kondensator als Topf mit einer Grundfläche von 6 mF und einer Füllhöhe von 20 V. Der zweite Kondensator bildet einen Topf mit 4 mF Querschnitt und einer Füllhöhe von -7.5 V. (Wir denken uns nun den Punkt zwischen den beiden Kapazitäten geerdet, das heisst auf dem Potenzial 0 V.) Nach dem Ausgleich müssen beide Töpfen gleich hoch gefüllt sein. Die im Widerstand dissipierte Energie entspricht der von der Ladung beim Hinunterfallen freigesetzten Energie (Ladungsmenge mal mittlere Fallhöhe). |
|||
| ⚫ | #Die Ladung des grossen Kondensators beträgt nach dem Entladen 54 mC, die des kleinen 36 mC. Das Vorzeichen ist Konvention |
||
#Nach dem Entladen verteilt sich die gesamte Ladung von 6 mF * 20 V + 4 mF * -7.5 V = 90 mC so auf beide Kondensatoren, dass beide die gleiche Spannung von 90 mC / (6 mF + 4 mF) = 9 V haben. Die Spannung über dem ersten Kondensator verkleinert sich um 11 V. Die Spannung über dem zweiten Kondensator steigt von -7.5 V um 16.5 V auf +9 V. Bezogen auf die eingezeichneten Spannungspfeile sinkt sie von 7.5 V um 16.5 V auf -9 V. |
|||
| ⚫ | #Im Entladevorgang "fallen" 66 mC über eine mittlere Spannung von 13.75 V. Folglich werden 908 mJ Energie frei gesezt. Diese Energie würde ein einzelner Kondensator mit einer Kapazität von 2.4 mF (Kapazität der Serieschaltung von 6 mF und 4 mF) ebenfalls freisetzen, wenn man ihn aus einer Anfangsspannung von 27.5 V vollständig entladen würde. |
||
| ⚫ | #Die Ladung des grossen Kondensators beträgt nach dem Entladen 6 mF * 9 V = 54 mC, die des kleinen 4 mF * -9 V = -36 mC. Das Vorzeichen ist Konvention. Da die totale Kondensatorladung immer gleich Null ist, speichert jeder Kondensator gleich viel Ladungsüberschuss wie Ladungsmangel. In diesem Beispiel müsste man bei der zweiten Ladung ein Minuszeichen setzen, falls man sich auf die eingezeichneten Spannungspfeile bezieht. Im [[Flüssigkeitsbild]] werden beide Ladungen positiv. |
||
| ⚫ | |||
| ⚫ | #Im Entladevorgang "fallen" 6 mF * (20 V - 9 V) = 66 mC über eine mittlere Spannung von [(20 V - (-7.5 V)) + 0]/2 = 13.75 V. Folglich werden 13.75 V * 66 mC = 908 mJ Energie frei gesezt und im Widerstand dissipiert. Diese Energie würde ein einzelner Kondensator mit einer Kapazität von 2.4 mF (Kapazität der Serieschaltung von 6 mF und 4 mF) ebenfalls freisetzen, wenn man ihn aus einer Anfangsspannung von 27.5 V vollständig entladen würde: 2.4 mF * (27.5 V)<sup>2</sup>/2 = 908 mJ. Die beiden Kondensatoren dürfen bezüglich ihres dynamischen Verhaltens (Entladeverhalten und Energieumsatz) durch einen einzelnen Kondensator mit einer Kapazität von 2.4 mF und einer Anfangsspannung von 27.5 V ersetzt werden. |
||
| ⚫ | |||
'''[[RC-Glied mit zwei Kondensatoren|Aufgabe]]''' |
'''[[RC-Glied mit zwei Kondensatoren|Aufgabe]]''' |
||
Aktuelle Version vom 17. Januar 2012, 15:06 Uhr
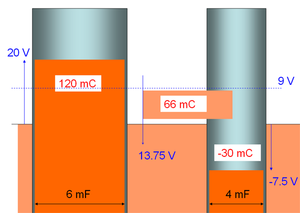
Im Flüssigkeitsbild erscheint der erste Kondensator als Topf mit einer Grundfläche von 6 mF und einer Füllhöhe von 20 V. Der zweite Kondensator bildet einen Topf mit 4 mF Querschnitt und einer Füllhöhe von -7.5 V. (Wir denken uns nun den Punkt zwischen den beiden Kapazitäten geerdet, das heisst auf dem Potenzial 0 V.) Nach dem Ausgleich müssen beide Töpfen gleich hoch gefüllt sein. Die im Widerstand dissipierte Energie entspricht der von der Ladung beim Hinunterfallen freigesetzten Energie (Ladungsmenge mal mittlere Fallhöhe).
- Nach dem Entladen verteilt sich die gesamte Ladung von 6 mF * 20 V + 4 mF * -7.5 V = 90 mC so auf beide Kondensatoren, dass beide die gleiche Spannung von 90 mC / (6 mF + 4 mF) = 9 V haben. Die Spannung über dem ersten Kondensator verkleinert sich um 11 V. Die Spannung über dem zweiten Kondensator steigt von -7.5 V um 16.5 V auf +9 V. Bezogen auf die eingezeichneten Spannungspfeile sinkt sie von 7.5 V um 16.5 V auf -9 V.
- Die Ladung des grossen Kondensators beträgt nach dem Entladen 6 mF * 9 V = 54 mC, die des kleinen 4 mF * -9 V = -36 mC. Das Vorzeichen ist Konvention. Da die totale Kondensatorladung immer gleich Null ist, speichert jeder Kondensator gleich viel Ladungsüberschuss wie Ladungsmangel. In diesem Beispiel müsste man bei der zweiten Ladung ein Minuszeichen setzen, falls man sich auf die eingezeichneten Spannungspfeile bezieht. Im Flüssigkeitsbild werden beide Ladungen positiv.
- Im Entladevorgang "fallen" 6 mF * (20 V - 9 V) = 66 mC über eine mittlere Spannung von [(20 V - (-7.5 V)) + 0]/2 = 13.75 V. Folglich werden 13.75 V * 66 mC = 908 mJ Energie frei gesezt und im Widerstand dissipiert. Diese Energie würde ein einzelner Kondensator mit einer Kapazität von 2.4 mF (Kapazität der Serieschaltung von 6 mF und 4 mF) ebenfalls freisetzen, wenn man ihn aus einer Anfangsspannung von 27.5 V vollständig entladen würde: 2.4 mF * (27.5 V)2/2 = 908 mJ. Die beiden Kondensatoren dürfen bezüglich ihres dynamischen Verhaltens (Entladeverhalten und Energieumsatz) durch einen einzelnen Kondensator mit einer Kapazität von 2.4 mF und einer Anfangsspannung von 27.5 V ersetzt werden.
- Die Zeitkonstante ist τ = 3 MΩ * 2.4 mF = 7200 s.