Magnusrolle: Unterschied zwischen den Versionen

Inhalt hinzugefügt Inhalt gelöscht

Inline

Aktuelle Version vom 4. Juni 2008, 04:48 Uhr

Das Objekt

Ein Hohlzylinder aus Karton wird mit Hilfe eines aufgewickelten Stoffbandes weggeschleudert und gleichzeitig in Rotation versetzt. Abhängig vom Wicklungssinn des Bandes steigt der Zylinder auf oder fliegt sehr schnell zu Boden. Mit etwas Übung bringt man den rotierenden Zylinder auf eine schleifenförmige Bahn (Looping). Diese verblüffende Bahnabweichung des rotierenden Körpers, die bei vielen Ballspielen bewusst eingesetzt wird, heisst Magnus-Effekt.

Theorie

Auf den rotierenden Zylinder wirken drei Kräfte ein, die Gewichtskraft (Impulsaustausch über das Gravitationsfeld), der Luftwiderstand und die Magnus-Effekt Magnuskraft. Luftwiderstand und Magnuskraft gehören ursächlich zusammen. Der Luftwiderstand ist der dissipativ wirkende Anteil des Impulsaustausches mit der Luft; der Luftwiderstand wirkt folglich gegen die momentane Anströmmgeschwindigkeit. Die Magnuskraft ist die normal zur Geschwindigkeit stehende Komponente der Luftkraft.

Anhand einer einfachen Energieüberlegung kann für den Luftwiderstand eine Näherungsformel abgeleitet werden. Um den Einfluss der Körperform (Zylinder, Kugel, Halbkugel) zu beschreiben, wird ein zusätzlicher Formfaktor (Widerstandsbeiwert c_W) eingeführt. Widerstandswert und Querschnittsfläche dürfen zur effektiven Fläche zusammengefasst werden

[math]\vec F_W = -\frac {\rho}{2} c_W A_{quer} |\vec v| \vec v = -\frac {\rho}{2} A_{eff} |\vec v| \vec v[/math]

Die Magnus-Effekt hängt von der Winkelgeschwindigkeit des Zylinders und von der Anströmgeschwindigkeit ab. Für die speziellen Eigenheiten des Körpers wird ein zweiten Formfaktor eingeführt

[math] \vec F_M=2c_M V\rho(\vec\omega\times\vec v)=\pi c_M\rho rA_{quer}(\vec\omega\times\vec v)[/math]

Die Luft bremst über die mitgerissene Grenzschicht die Rotation des Zylinders. Mangels exakter Theorie machen wir für das auf den Zylinder einwirkende Drehmoment eine plausible Abschätzung. Die Unsicherheiten bezüglich der Wirkung steckt im dritten Formfaktor (c_R)

[math]M = \frac {\rho}{2} r^3 c_R A_{quer} \omega^2[/math]

Simulationsmodell

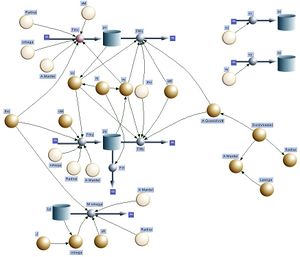
Das Grundgerüst des Simulationsmodells wird von drei Bilanzgleichungen gebildet, den Impulsbilanzen für die Horizontal- und die Vertikalkomponente sowie der Drehimpulsbilanz.

Die x-Impulsbilanz fasst die x-Komponenten des Luftwiderstandes und der Magnuskraft zur Impulsänderungsrate zusammen. Bei der Bilanz der vertikalen Komponente kommt noch der Impulsaustausch mit dem Gravitationsfeld, die Gewichtskraft, dazu. In der Drehimpulsbilanz erscheint nur der Drehimpulsaustausch zwischen Luft und Körper, wobei de Stärke dieses Drehimpulsstromes auch Reibdrehmoment genannt wird. Die Integration der Schwerpunktsgeschwindigkeit über die Zeit, mit der die aktuelle Position berechnete wird, liefert zwei weiteren Fluss-Topf-Strukturen. Im Gegensatz zu den "Bilanztöpfen" speichern die beiden "Ortstöpfe" keine eigentliche Menge. Die Integration der Geschwindigkeit zum Ort ist eine rein geometrische Angelegenheit. Weil die Definition der Geschwindigkeit als Änderungsrate des Ortes definiert ist, muss der "Geschwindigkeitsfluss" immer in den "Ortstopf" hinein zeigen.

Die konstitutiven Gesezte sind entweder grundlegend (Masse und Massenträgheitsmoment als Kapazitäten) oder oben schon diskutiert worden. Beim Start ist die Geschwindigkeit horizontal gerichtet und die Winkelgeschwindigkeit ist gleich Geschwindigkeitsbetrag dividiert durch Zylinderradius (Rollbedingung).

Eine zweite Modellierung dieses Problems ist in der Vorlesung Mechanik des starren Körpers im Studiengang Aviatik zu finden. Der Magnus-Effekt tritt auch beim Fussball und beim Tennisball auf.

Simulation

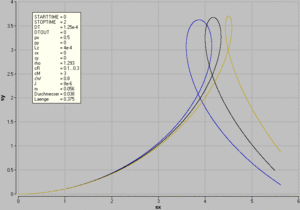
Der Widerstandsbeiwert kann einer Tabellensammlung entnommen werden. Die beiden andern Formfaktoren sind anhand der experimentellen Erfahrung geschätzt worden. Die Graphik zeigt eine Parameterstudie für den Formfaktor des reibenden Drehmoments. Im hier verwendeten Modell ist im Unterschied zur oben aufgeführten Formel der Faktor π im Formfaktor c_M enthalten. Wäre die oben aufgeführten Formel verwendet worden, würde der Formfaktor c_M=0.955 betragen.

@@ Zeile 1: / Zeile 1: @@
 ==Das Objekt==
-Ein Hohlzylinder aus Karton wird mit Hilfe eines aufgewickelten Stoffbandes weggeschleudert und gleichzeitig in Rotation versetzt. Abhängig vom Wicklungssinn des Bandes steigt der Zylinder auf oder fliegt sehr schnell zu Boden. Mit etwas Übung bringt man den rotierenden Zylinder auf eine schleifenförmige Bahn (Looping). Diese verblüffende Bahnabweichung des rotierenden Körpers, die bei vielen [[Fussball|Ballspielen]] bewusst eingesetzt wird, heisst Magnuseffekt.
+Ein Hohlzylinder aus Karton wird mit Hilfe eines aufgewickelten Stoffbandes weggeschleudert und gleichzeitig in Rotation versetzt. Abhängig vom Wicklungssinn des Bandes steigt der Zylinder auf oder fliegt sehr schnell zu Boden. Mit etwas Übung bringt man den rotierenden Zylinder auf eine schleifenförmige Bahn (Looping). Diese verblüffende Bahnabweichung des rotierenden Körpers, die bei vielen [[Fussball|Ballspielen]] bewusst eingesetzt wird, heisst [[Magnus-Effekt]].
 ==Theorie==
@@ Zeile 7: / Zeile 7: @@
 Anhand einer einfachen Energieüberlegung kann für den [[Luftwiderstand]] eine Näherungsformel abgeleitet werden. Um den Einfluss der Körperform (Zylinder, Kugel, Halbkugel) zu beschreiben, wird ein zusätzlicher Formfaktor (Widerstandsbeiwert ''c<sub>W</sub>'') eingeführt. Widerstandswert und Querschnittsfläche dürfen zur effektiven Fläche zusammengefasst werden
-<math>\vec F_W = -\frac {\rho}{2} c_W A_{quer} |\vec v| \vec v = -\frac {\rho}{2} A_{eff} |\vec v| \vec v</math>
+:<math>\vec F_W = -\frac {\rho}{2} c_W A_{quer} |\vec v| \vec v = -\frac {\rho}{2} A_{eff} |\vec v| \vec v</math>
 Die [[Magnus-Effekt]] hängt von der [[Winkelgeschwindigkeit]] des Zylinders und von der Anströmgeschwindigkeit ab. Für die speziellen Eigenheiten des Körpers wird ein zweiten Formfaktor eingeführt
-<math>\vec F_M = \rho r c_M A_{quer} (\vec \omega x \vec v)</math>
+:<math> \vec F_M=2c_M V\rho(\vec\omega\times\vec v)=\pi c_M\rho rA_{quer}(\vec\omega\times\vec v)</math>
 Die Luft bremst über die mitgerissene Grenzschicht die Rotation des Zylinders. Mangels exakter Theorie machen wir für das auf den Zylinder einwirkende Drehmoment eine plausible Abschätzung. Die Unsicherheiten bezüglich der Wirkung steckt im dritten Formfaktor (''c<sub>R</sub>'')
-<math>M = \frac {\rho}{2} r^3 c_R A_{quer} \omega^2</math>
+:<math>M = \frac {\rho}{2} r^3 c_R A_{quer} \omega^2</math>
 ==Simulationsmodell==
 [[Bild:Magnusrolle_SD.jpg|thumb|Systemdiagramm der Magnusrolle]]
-Das Grundgerüst des Simulationsmodells wird von drei Bilanzgleichungen gebildet, den [[Impulsbilanz|Impulsbilanzen]] für die zwei Richtungen sowie der zugehörigen [[Drehimpulsbilanz]].
+Das Grundgerüst des Simulationsmodells wird von drei Bilanzgleichungen gebildet, den [[Impulsbilanz|Impulsbilanzen]] für die Horizontal- und die Vertikalkomponente sowie der [[Drehimpulsbilanz]].
-Die Bilanz der horizontalen Impulskomponente fasst die entsprechenden Komponenten des Luftwiderstandes und der Magnuskraft zur Impulsänderungsrate zusammen. Bei der Bilanz der vertikalen komponente kommt noch der Impulsaustausch mit dem Gravitationsfeld dazu. In der Drehimpulsbilanz erscheint nur der Drehimpulsaustausch zwischen Luft und Körper. Neben den drei Bilanzgleichungen führt die Integration der Schwerpunktsgeschwindigkeit zur Position noch zu zwei weiteren Fluss-Topf- (flow-stock-) Strukturen.
+Die ''x''-Impulsbilanz fasst die ''x''-Komponenten des Luftwiderstandes und der Magnuskraft zur Impulsänderungsrate zusammen. Bei der Bilanz der vertikalen Komponente kommt noch der Impulsaustausch mit dem Gravitationsfeld, die Gewichtskraft, dazu. In der Drehimpulsbilanz erscheint nur der Drehimpulsaustausch zwischen Luft und Körper, wobei de Stärke dieses Drehimpulsstromes auch Reibdrehmoment genannt wird. Die Integration der Schwerpunktsgeschwindigkeit über die Zeit, mit der die aktuelle Position berechnete wird, liefert zwei weiteren Fluss-Topf-Strukturen. Im Gegensatz zu den "Bilanztöpfen" speichern die beiden "Ortstöpfe" keine eigentliche Menge. Die Integration der Geschwindigkeit zum Ort ist eine rein geometrische Angelegenheit. Weil die Definition der Geschwindigkeit als Änderungsrate des Ortes definiert ist, muss der "Geschwindigkeitsfluss" immer in den "Ortstopf" hinein zeigen.
-Die konstitutiven Gesezte sind entweder grundlegend ([[Masse]] und [[Massenträgheitsmoment]] als [[kapazitives Gesetz|Kapazitäten]]) oder weiter oben schon diskutiert worden. Beim Start ist die Geschwindigkeit horizontal gerichtet und die Winkelgeschwindigkeit ist gleich Geschwindigkeitsbetrag dividiert durch Zylinderradius.
+Die konstitutiven Gesezte sind entweder grundlegend ([[Masse]] und [[Massenträgheitsmoment]] als [[kapazitives Gesetz|Kapazitäten]]) oder oben schon diskutiert worden. Beim Start ist die Geschwindigkeit horizontal gerichtet und die Winkelgeschwindigkeit ist gleich Geschwindigkeitsbetrag dividiert durch Zylinderradius (Rollbedingung).
+Eine zweite Modellierung dieses Problems ist in der Vorlesung [[Mechanik des starren Körpers]] im Studiengang [[Aviatik]] zu finden. Der [[Magnus-Effekt]] tritt auch beim [[Fussball]] und beim [[Tennisball]] auf.
 ==Simulation==
 [[Bild:Magnusrolle_xy.gif|thumb|Bahn der Magnusrolle]]
-Der Widerstandsbeiwert kann einem Tabellenbuch entnommen werden. Die beiden andern Formfaktoren sind anhand der experimentellen Erfahrung geschätz worden. Die Graphik zeigt eine Parameterstudie für den Formfaktor des reibenden Drehmoments.
+Der Widerstandsbeiwert kann einer Tabellensammlung entnommen werden. Die beiden andern Formfaktoren sind anhand der experimentellen Erfahrung geschätzt worden. Die Graphik zeigt eine Parameterstudie für den Formfaktor des reibenden Drehmoments. Im hier verwendeten Modell ist im Unterschied zur oben aufgeführten Formel der Faktor ''&pi;'' im Formfaktor ''c<sub>M</sub>'' enthalten. Wäre die oben aufgeführten Formel verwendet worden, würde der Formfaktor ''c<sub>M</sub>''=0.955 betragen.
 [[Kategorie:Trans]] [[Kategorie:Rot]] [[Kategorie:Modelle]] [[Kategorie:TransMod]] [[Kategorie:RotMod]]