Lösung zu Rangierstoss 2: Unterschied zwischen den Versionen
Inhalt hinzugefügt Inhalt gelöscht
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (4 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Bild:Rangierstoss_2.jpg|thumb|Flüssigkeitsbild des Rangierstosses]] |
|||
Zwei wichtige Zusammenhänge können direkt dem [[Flüssigkeitsbild]] entnommen werden: |
|||
*Die Impulsänderung ist gleich Masse mal Geschwindigkeitsänderung: <math>\Delta p_x = m \Delta v_x</math> |
|||
*Die |
*Die Impulsänderung ist gleich Masse mal Geschwindigkeitsänderung: <math> \Delta p_x = m \Delta v_x</math> |
||
*Die Impulsänderungsrate ist gleich Masse mal Geschwindigkeitsänderungsrate (Beschleunigung): <math>\dot p_x = m \dot v_x</math> |
|||
#Im Flüssigkeitsbild erscheint die Geschwindigkeit als Höhe und die Beschleunigung als Geschwindigkeit des Flüssigkeitsspiegels. Die Sinkgeschwindigkeit des Flüssigkeitsspiegels im ersten Gefäss oder die Steiggeschwindigkeit des Flüssigkeitsspiegels im zweiten Gefäss entsprechen den Beschleunigungen der beiden Wagen. Anfänglich sinkt der Spiegel im ersten Gefäss immer schneller ab. Dementsprechend fliesst immer mehr Impuls durch die Puffer. Sobald die Wagen gleich schnell geworden sind, nimmt die Stärke des Impulsstromes schlagartig ab. Danach geht die Impulsstromstärke gegen Null. Solange die Geschwindigkeit des auflaufenden Wagens grösser als die des anfänglich stehenden ist, fahren die Puffer ein; danach werden sie wieder länger. Weil in den Puffern eine kraftabhängige Reibung wirkt, verändert sich der durchfliessende Impulsstrom beim Übergang vom Ein- zum Ausfahren schlagartig. |
|||
#Aus dem Geschwindigkeits-Zeit-Diagramm kann man die Beschleunigung als Geschwindigkeitsänderungsrate oder Steigung der Geschwindigkeits-Zeit-Kurve entnehmen. Die Steigung berechnet man als Differenzenquotient, indem man eine Tangente in das Diagramm zeichnet, die bis an den Diagrammrand reicht. Das ergibt zum Zeitpunkt 0.05 s eine Beschleunigung des ersten Wagens von etwa (0.3 m/s - 2.2 m/s) / 0.3 s = -6.3 m/s<sup>2</sup>. Für den zweiten Wagen erhält man ca. 2.5 m/s /(0.17 s - 0.02 s) = 17 m/s<sup>2</sup>. |
|||
#Die Impulsstromstärke oder resultierende Pufferkraft ist gleich der Impulsänderungsrate des ersten (minus) oder des zweiten Wagens (plus). Die Impulsänderungsrate ist gleich Masse mal Beschleunigung. Zum Zeitpunkt 0.05 s beträgt die Impulsänderungsrate im ersten Wagen etwa 80'000 kg * -6.3 m/s<sup>2</sup> = -500 kN. Der durch die Puffer fliessende Impulsstrom beträgt also ca. 500 kN. |
|||
#Weil die Impulsänderungsraten beider Wagen entgegengesetzt gleich sind, muss das Produkt aus Masse und Betrag der Beschleunigung für beide Wagen gleich sein. Folglich gilt <math> m_2 = \frac {|a_1|}{a_2}m_1 = \frac {|-6.3 m/s^2|}{17 m/s^2}m_1 = 30 t</math>. |
|||
Das systemdynamische Modell zu dieser Aufgabe finden Sie unter [[Auflaufstoss]]. |
|||
'''[[Rangierstoss 2|Aufgabe]]''' |
'''[[Rangierstoss 2|Aufgabe]]''' |
||
Aktuelle Version vom 17. Juli 2009, 09:36 Uhr
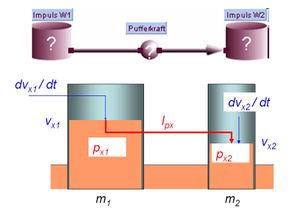
Zwei wichtige Zusammenhänge können direkt dem Flüssigkeitsbild entnommen werden:
- Die Impulsänderung ist gleich Masse mal Geschwindigkeitsänderung: [math] \Delta p_x = m \Delta v_x[/math]
- Die Impulsänderungsrate ist gleich Masse mal Geschwindigkeitsänderungsrate (Beschleunigung): [math]\dot p_x = m \dot v_x[/math]
- Im Flüssigkeitsbild erscheint die Geschwindigkeit als Höhe und die Beschleunigung als Geschwindigkeit des Flüssigkeitsspiegels. Die Sinkgeschwindigkeit des Flüssigkeitsspiegels im ersten Gefäss oder die Steiggeschwindigkeit des Flüssigkeitsspiegels im zweiten Gefäss entsprechen den Beschleunigungen der beiden Wagen. Anfänglich sinkt der Spiegel im ersten Gefäss immer schneller ab. Dementsprechend fliesst immer mehr Impuls durch die Puffer. Sobald die Wagen gleich schnell geworden sind, nimmt die Stärke des Impulsstromes schlagartig ab. Danach geht die Impulsstromstärke gegen Null. Solange die Geschwindigkeit des auflaufenden Wagens grösser als die des anfänglich stehenden ist, fahren die Puffer ein; danach werden sie wieder länger. Weil in den Puffern eine kraftabhängige Reibung wirkt, verändert sich der durchfliessende Impulsstrom beim Übergang vom Ein- zum Ausfahren schlagartig.
- Aus dem Geschwindigkeits-Zeit-Diagramm kann man die Beschleunigung als Geschwindigkeitsänderungsrate oder Steigung der Geschwindigkeits-Zeit-Kurve entnehmen. Die Steigung berechnet man als Differenzenquotient, indem man eine Tangente in das Diagramm zeichnet, die bis an den Diagrammrand reicht. Das ergibt zum Zeitpunkt 0.05 s eine Beschleunigung des ersten Wagens von etwa (0.3 m/s - 2.2 m/s) / 0.3 s = -6.3 m/s2. Für den zweiten Wagen erhält man ca. 2.5 m/s /(0.17 s - 0.02 s) = 17 m/s2.
- Die Impulsstromstärke oder resultierende Pufferkraft ist gleich der Impulsänderungsrate des ersten (minus) oder des zweiten Wagens (plus). Die Impulsänderungsrate ist gleich Masse mal Beschleunigung. Zum Zeitpunkt 0.05 s beträgt die Impulsänderungsrate im ersten Wagen etwa 80'000 kg * -6.3 m/s2 = -500 kN. Der durch die Puffer fliessende Impulsstrom beträgt also ca. 500 kN.
- Weil die Impulsänderungsraten beider Wagen entgegengesetzt gleich sind, muss das Produkt aus Masse und Betrag der Beschleunigung für beide Wagen gleich sein. Folglich gilt [math] m_2 = \frac {|a_1|}{a_2}m_1 = \frac {|-6.3 m/s^2|}{17 m/s^2}m_1 = 30 t[/math].
Das systemdynamische Modell zu dieser Aufgabe finden Sie unter Auflaufstoss.