2 LKF mit Teleskopstange: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
K (Leerschlag bei Gleichungen eingefügt) |
||
| (Eine dazwischenliegende Version von einem anderen Benutzer wird nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
Die Impulsbilanz bildet den Kern dieses systemdynamischen Modells. Das in der Teleskopstange wirkende Kraftgesetz kann wie eine [[Gleitreibung]] modelliert werden |
Die Impulsbilanz bildet den Kern dieses systemdynamischen Modells. Das in der Teleskopstange wirkende Kraftgesetz kann wie eine [[Gleitreibung]] modelliert werden |
||
<math>I_p = F_{max} \frac {2}{pi} \arctan(1000 (v_2 - v_1))</math> |
<math> I_p = F_{Tele} = F_{max} \frac {2}{pi} \arctan(1000 (v_2 - v_1))</math> |
||
Der Faktor 1000, der das Argument der Arcustangens-Funktion dehnt, kann auch grösser oder kleiner gewählt werden. Nur muss dann der Zeitschritt bei der Simulation entsprechend angepasst werden. |
Der Faktor 1000, der das Argument der Arcustangens-Funktion dehnt, kann auch grösser oder kleiner gewählt werden. Nur muss dann der Zeitschritt bei der Simulation entsprechend angepasst werden. |
||
Aktuelle Version vom 27. November 2007, 23:19 Uhr
System
Zwei ruhende Luftkissenfahrzeuge (750 g und 250 g) sind über eine Teleskopstange miteinander verbunden. Diese Teleskopstange besteht aus zwei ineinander geschobenen Röhrchen, die einen Impulsstrom von maximal 6 N zu übertragen vermögen: bei einer Belastung von weniger als 6 N verhält sich die Stange wie ein starrer Stab; bei 6 N beginnt sich die Teleskopstange zu verlängern. Am rechten, leichteren Fahrzeug greift nun über eine Schnur eine nach rechts gerichtete Kraft an, die in 0.25 s linear von Null auf 20 N anwächst und dann plötzlich wieder auf Null abfällt.
Modell
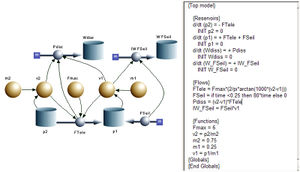
Die Impulsbilanz bildet den Kern dieses systemdynamischen Modells. Das in der Teleskopstange wirkende Kraftgesetz kann wie eine Gleitreibung modelliert werden
[math] I_p = F_{Tele} = F_{max} \frac {2}{pi} \arctan(1000 (v_2 - v_1))[/math]
Der Faktor 1000, der das Argument der Arcustangens-Funktion dehnt, kann auch grösser oder kleiner gewählt werden. Nur muss dann der Zeitschritt bei der Simulation entsprechend angepasst werden.
Die Leistung der Seilkraft, der dem Impulsstrom zugeordnete Energiestrom, wird zur Arbeit der Seilkraft und die Prozessleistung in der Teleskopstange zur dissipierten Energie aufintegriert.
Simulation
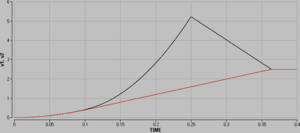
Zum Zeitpunkt 0.1 s, dann wenn über das Seil ein Impulsstrom der Stärke 8 N zufliesst, beginnt sich das Teleskoprohr zu verlängern. Danach erhöht sich die Geschwindigkeit des leichteren Fahrzeuges schneller als die des schwereren. Nach 0.25 s beginnnen sich die Geschwindigkeit wieder anzugleichen. Weil dann der Impuls mit einer Stärke von 6 N durch den Teleskopstange strömt, erfährt das leichtere Fahrzeug eine Beschleunigung von -24 m/s2 und das schwerere wird mit 8 m/s2 beschleunigt. Die zwischen den beiden Kurven liegende Fläche entspricht der Verlängerung des Teleskopverbindung.
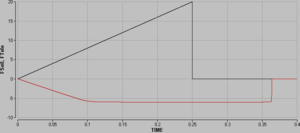
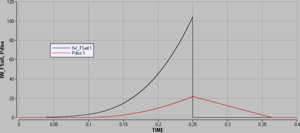
Solange der durch die Teleskopstange fliessende Impulsstrom schwächer als 6 N ist, fliessen 75% des über das Seil zugeführten Impulses an das schwerere Luftkissenfahrzeug weiter. Sobald die Grenze von 6 N erreicht ist, wird dieser Strom beibehalten. Erst wenn beide Fahrzeuge wieder gleich schnell sind, geht auch dieser Impulsstrom auf Null zurück. Das Vorzeichen der Impulsströme richten sich nach der Richtung des Rohres (flow) im Systemdiagramm.