Stoss: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) |
||
| (6 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 15: | Zeile 15: | ||
Beim inelastischen Stoss fliesst der Impuls vom Körper mit der grösseren zum Körper mit der kleineren Geschwindigkeit, bis sich die Geschwindigkeiten angeglichen haben. Im Flüssigkeitsbild erscheint der inelastische Stoss als Niveauausgleich. Die vom Impuls in der Stosszone freigesetzte Energie wird [[Dissipation|dissipiert]]. Die Formel für die Endgeschwindigkeit und die dissipierte Energie können direkt dem Flüssigkeitsbild entnommen werden |
Beim inelastischen Stoss fliesst der Impuls vom Körper mit der grösseren zum Körper mit der kleineren Geschwindigkeit, bis sich die Geschwindigkeiten angeglichen haben. Im Flüssigkeitsbild erscheint der inelastische Stoss als Niveauausgleich. Die vom Impuls in der Stosszone freigesetzte Energie wird [[Dissipation|dissipiert]]. Die Formel für die Endgeschwindigkeit und die dissipierte Energie können direkt dem Flüssigkeitsbild entnommen werden |
||
:<math>v_{in} |
:<math>v_{in}=\frac{m_1 v_1+m_2 v_2}{m_1+m_2}</math> |
||
| ⚫ | |||
| ⚫ | |||
===vollelastisch=== |
===vollelastisch=== |
||
[[Bild:VollelastischerStoss.png|thumb|Flüssigkeitsbild eines vollelastischen Sosses]] |
[[Bild:VollelastischerStoss.png|thumb|Flüssigkeitsbild eines vollelastischen Sosses]] |
||
Beim vollelastischen Stoss setzt der Impuls bis zum Ausgleich der Geschwindigkeiten Energie frei. Diese Energie wird in der vollelastischen Stosszone (Feder, Gummi) zwischengespeichert. In der zweiten Stossphase, dann wenn sich die Feder oder der Gummi wieder entspannen, wird nochmals soviel Impuls wie in der ersten Phase vom anfänglich schnelleren in den andern Körper gepumpt. Im Flüssigkeitsbild erscheint der vollelastische Stoss als ein Überschwingen der beiden Flüssigkeitssäulen. Um den Endzustand zu bestimmen, spiegelt man die beiden Flüssigkeitsoberflächen am inelastischen Zustand, d.h. man klappt die Relativgeschwindigkeiten auf die andere Seite der " |
Beim vollelastischen Stoss setzt der Impuls bis zum Ausgleich der Geschwindigkeiten Energie frei. Diese Energie wird in der vollelastischen Stosszone (Feder, Gummi) zwischengespeichert. In der zweiten Stossphase, dann wenn sich die Feder oder der Gummi wieder entspannen, wird nochmals soviel Impuls wie in der ersten Phase vom anfänglich schnelleren in den andern Körper gepumpt. Im Flüssigkeitsbild erscheint der vollelastische Stoss als ein Überschwingen der beiden Flüssigkeitssäulen. Um den Endzustand zu bestimmen, spiegelt man die beiden Flüssigkeitsoberflächen am inelastischen Zustand, d.h. man klappt die Relativgeschwindigkeiten auf die andere Seite der "inelastischen Linie". |
||
Rein formal kann der |
Rein formal kann der vollelastische Stoss mittels Impuls- und Energieerhaltung (vorher gleich nachher) formuliert werden |
||
:<math>p_{tot} |
:<math>p_{tot}=p_{1v}+p_{2v}=p_{1n}+p_{2n}</math> |
||
:<math>W_{kin } |
:<math>W_{kin }=\frac{(p_{1v})^2}{2m_1}+\frac{(p_{2v})^2}{2m_2}=\frac{(p_{1n})^2}{2m_1}+\frac{(p_{2n})^2}{2m_2}</math> |
||
===teilelastisch=== |
===teilelastisch=== |
||
| Zeile 34: | Zeile 33: | ||
Der teilelastische oder reale Stoss liegt zwischen dem inelastischen und dem vollelastischen. Das Verhältnis zwischen der vom Impuls in der zweiten Phase aufgenommenen Energie zur vorher freigesetzten heisst Stosszahl. Weil die umgesetzte Energie proportional zum geflossenen Impuls und proportional zur Differenz der Anfangs- bzw. Endgeschwindigkeiten der beiden Körper ist, wächst der Energieumsatz quadratisch mit den Relativgeschwindigkeiten |
Der teilelastische oder reale Stoss liegt zwischen dem inelastischen und dem vollelastischen. Das Verhältnis zwischen der vom Impuls in der zweiten Phase aufgenommenen Energie zur vorher freigesetzten heisst Stosszahl. Weil die umgesetzte Energie proportional zum geflossenen Impuls und proportional zur Differenz der Anfangs- bzw. Endgeschwindigkeiten der beiden Körper ist, wächst der Energieumsatz quadratisch mit den Relativgeschwindigkeiten |
||
:Stosszahl <math>\eta |
:Stosszahl <math>\eta=\frac{W_{auf}}{W_{frei}}=\frac{(v_{nach}-v_{in})^2}{(v_{vor}-v_{in})^2}</math> |
||
Die Stosszahl ist für viele Materialien und in bestimmten Grenzen näherungsweise geschwindigkeitsunabhängig. Bei [[Auflaufstoss|Güterwagen]] beträgt die Stosszahl etwa 0.33. |
Die Stosszahl ist für viele Materialien und in bestimmten Grenzen näherungsweise geschwindigkeitsunabhängig. Bei [[Auflaufstoss|Güterwagen]] beträgt die Stosszahl etwa 0.33. |
||
==zentraler Stoss== |
==zentraler Stoss== |
||
===Erhaltungsgrössen=== |
|||
Beim zentralen Stoss wird Impuls, aber kein Drehimpuls übertragen. Der zentrale Stoss kann auf den geraden Stoss zurückgeführt werden, indem z.B. die ''x''-Achse des Koordinatensystems in Stossrichtung gelegt wird. Für die ''x''-Komponente des Impulses gelten dann die Überlegungen des geraden Stosses. Die andern beiden Impuls-Komponenten werden nicht ausgetauscht und bleiben in den Stosspartnern drin. |
Beim zentralen Stoss wird Impuls, aber kein Drehimpuls übertragen. Der zentrale Stoss kann auf den geraden Stoss zurückgeführt werden, indem z.B. die ''x''-Achse des Koordinatensystems in Stossrichtung gelegt wird. Für die ''x''-Komponente des Impulses gelten dann die Überlegungen des geraden Stosses. Die andern beiden Impuls-Komponenten werden nicht ausgetauscht und bleiben in den Stosspartnern drin. |
||
Mathematisch kann der zentrale Stoss durch die Impulserhaltung beschrieben werden |
Mathematisch kann der zentrale Stoss durch die Impulserhaltung beschrieben werden |
||
:<math>\begin{pmatrix}p_{xtot} |
:<math>\begin{pmatrix}p_{xtot}\\ p_{ytot}\\ p_{ztot}\end{pmatrix}=\begin{pmatrix}p_{x1v}\\p_{y1v}\\p_{z1v}\end{pmatrix}+\begin{pmatrix}p_{x2v} \\ p_{y2v}\\p_{z2v}\end{pmatrix}=\begin{pmatrix}p_{x1n}\\ p_{y1n}\\p_{z1n}\end{pmatrix}+\begin{pmatrix}p_{x2n}\\p_{y2n}\\ p_{z2n}\end{pmatrix}</math> |
||
Handelt es sich um einen elastischen Stoss, bleibt zusätzlich noch die kinetische Energie erhalten |
Handelt es sich um einen elastischen Stoss, bleibt zusätzlich noch die kinetische Energie erhalten |
||
:<math>W_{kin } |
:<math>W_{kin }=\frac{(\vec p_{1v})^2}{2m_1}+\frac{(\vec p_{2v})^2}{2m_2}=\frac{(\vec p_{1n})^2}{2m_1}+\frac{(\vec p_{2n})^2}{2m_2}</math> |
||
===Massenmittelpunkt=== |
|||
Sind der Anfangsimpuls der beiden Stosspartner sowie die Massen gegeben, schränkt die Impulserhaltung den Endzustand bis auf drei unabhängige, skalare Grössen ein. Beobachtet man nun den Vorgang von einem System aus, das sich mit dem [[Massenmittelpunkt]] (''MMP'') bewegt, bleibt der Impuls der beiden Partner während des ganzen Stossvorganges gleich Null. In ''MMP''-Bezugssystem sind die beiden Impulsvektoren zu jedem Zeitpunkt entgegengesetzt gleich gross (diese Betrachtungsweise entspricht im [[Flüssigkeitsbild]] dem Bezug der Geschwindigkeiten auf ''v<sub>in</sub>''). |
|||
Der Betrag des Impulses der wegfliegenden Körper muss im ''MMP''-System kleiner oder gleich wie der Betrag des Impulses der Körper vor dem Stoss sein, weil die kinetische Energie infolge [[Dissipation]] nur abnehmen kann. Im auf den ''MMP'' bezogenen Impulsraum bilden die Impulsvektoren der beiden aufeinander zufliegenden Körper den Durchmesser einer Kugel. Liegt der Impuls nachher auf der Kugeloberläche, ist der Stoss elastisch, anderfalls reichen die beiden Impulsvektoren nicht bis zur Kugeloberfläche. |
|||
==schiefer Stoss== |
==schiefer Stoss== |
||
| Zeile 54: | Zeile 59: | ||
Mathematisch kann der schiefe Stoss durch die Impuls- und Drehimpulserhaltung beschrieben werden |
Mathematisch kann der schiefe Stoss durch die Impuls- und Drehimpulserhaltung beschrieben werden |
||
:<math>\begin{pmatrix}p_{xtot} |
:<math>\begin{pmatrix}p_{xtot}\\p_{ytot}\\p_{ztot}\end{pmatrix}=\begin{pmatrix}p_{x1v}\\p_{y1v}\\p_{z1v}\end{pmatrix}+\begin{pmatrix}p_{x2v}\\ p_{y2v}\\p_{z2v}\end{pmatrix}=\begin{pmatrix}p_{x1n}\\p_{y1n}\\p_{z1n}\end{pmatrix}+\begin{pmatrix}p_{x2n}\\p_{y2n}\\p_{z2n}\end{pmatrix}</math> |
||
:<math>\begin{pmatrix}L_{xtot} |
:<math>\begin{pmatrix}L_{xtot}\\L_{ytot}\\L_{ztot}\end{pmatrix}=\begin{pmatrix}L_{x1v}\\L_{y1v}\\L_{z1v}\end{pmatrix}+\begin{pmatrix}L_{x2v}\\L_{y2v}\\L_{z2v}\end{pmatrix}=\begin{pmatrix}L_{x1n}\\ L_{y1n}\\L_{z1n}\end{pmatrix}+\begin{pmatrix}L_{x2n}\\ L_{y2n}\\L_{z2n}\end{pmatrix}</math> |
||
| Zeile 62: | Zeile 67: | ||
==relativistischer Stoss== |
==relativistischer Stoss== |
||
Nähert sich die Bewegung der Körper der Lichtgeschwindigkeit, machen sich die relativistischen Effekte bemerkbar. [[Energie]] (gleich Masse) und [[Impuls]] bilden dann gemeinsam einen vierdimensionalen Vektor in der [[Raum-Zeit]]. Um die vierte, die zeitliche Komponente dieses Vektors zu berechnen, multipliziert man die Masse mit der Lichtgeschwindigkeit oder dividiert die Gesamtenergie des Körpers mit der Lichtgeschwindigkeit |
|||
<math>p_T=m c=\frac {W}{c}</math> |
|||
Stossen treffen Körper mit hoher Geschwindigkeit aufeinander, bleibt jede dieser vier Grössen erhalten |
|||
:<math>\begin{pmatrix}p_{Ttot}\\p_{xtot}\\p_{ytot}\\p_{ztot}\end{pmatrix}=\begin{pmatrix}p_{T1v}\\p_{x1v}\\p_{y1v}\\p_{z1v}\end{pmatrix}+\begin{pmatrix}p_{T2v}\\p_{x2v}\\p_{y2v}\\p_{z2v}\end{pmatrix}=\begin{pmatrix}p_{T1n}\\ p_{x1n}\\p_{y1n}\\ p_{z1n}\end{pmatrix}+\begin{pmatrix}p_{T2n} \\ p_{x2n}\\p_{y2n}\\p_{z2n}\end{pmatrix}</math> |
|||
==Elementarteilchen== |
==Elementarteilchen== |
||
==Links== |
|||
*[http://www.youtube.com/watch?v=Pwoaqmxu4as unelastischer Stoss] auf Youtube |
|||
*[http://www.youtube.com/watch?v=jFI5cFzjg0U elastischer Stoss] auf Youtube |
|||
[[Kategorie:Trans]] |
[[Kategorie:Trans]] |
||
Aktuelle Version vom 6. Dezember 2012, 05:00 Uhr
Ein Stoss ist eine kurze Wechselwirkung zwischen zwei Körpern. Bei einem Stoss wird Impuls und Drehimpuls übertragen. Die vom Impulsstrom freigesetzte Energie wird teilweise dissipiert.
Man unterscheidet zwischn
- schiefer oder versetzter Stoss: es wird Impuls und Drehimpuls übertragen
- zentraler Stoss: es wird nur Impuls übertragen
- gerader Stoss: eindimensionales Stossproblem
- inelastischer Stoss: Energie wird maximal dissipiert
- vollelastischer Stoss: es wird keine Energie dissipiert
- teilelastischer Stoss: ein Teil der beim Austausch freigesetzten Energie wird dissipiert
gerader Stoss
Der gerade Stoss verläuft längs einer Geraden. Die Dynamik dieses Stosses lässt sich mit einer einzigen Impulskomponente beschreiben und im Flüssigkeitsbild darstellen.
inelastisch
Beim inelastischen Stoss fliesst der Impuls vom Körper mit der grösseren zum Körper mit der kleineren Geschwindigkeit, bis sich die Geschwindigkeiten angeglichen haben. Im Flüssigkeitsbild erscheint der inelastische Stoss als Niveauausgleich. Die vom Impuls in der Stosszone freigesetzte Energie wird dissipiert. Die Formel für die Endgeschwindigkeit und die dissipierte Energie können direkt dem Flüssigkeitsbild entnommen werden
- [math]v_{in}=\frac{m_1 v_1+m_2 v_2}{m_1+m_2}[/math]
- [math]W_{diss}=\Delta v_{mittel}\Delta p=\frac{(v_1-v_2)}{2}m_1(v_1-v_{in})=\frac{(v_1-v_2)}{2}m_2(v_2-v_{in})[/math]
vollelastisch
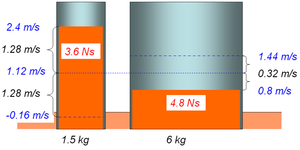
Beim vollelastischen Stoss setzt der Impuls bis zum Ausgleich der Geschwindigkeiten Energie frei. Diese Energie wird in der vollelastischen Stosszone (Feder, Gummi) zwischengespeichert. In der zweiten Stossphase, dann wenn sich die Feder oder der Gummi wieder entspannen, wird nochmals soviel Impuls wie in der ersten Phase vom anfänglich schnelleren in den andern Körper gepumpt. Im Flüssigkeitsbild erscheint der vollelastische Stoss als ein Überschwingen der beiden Flüssigkeitssäulen. Um den Endzustand zu bestimmen, spiegelt man die beiden Flüssigkeitsoberflächen am inelastischen Zustand, d.h. man klappt die Relativgeschwindigkeiten auf die andere Seite der "inelastischen Linie".
Rein formal kann der vollelastische Stoss mittels Impuls- und Energieerhaltung (vorher gleich nachher) formuliert werden
- [math]p_{tot}=p_{1v}+p_{2v}=p_{1n}+p_{2n}[/math]
- [math]W_{kin }=\frac{(p_{1v})^2}{2m_1}+\frac{(p_{2v})^2}{2m_2}=\frac{(p_{1n})^2}{2m_1}+\frac{(p_{2n})^2}{2m_2}[/math]
teilelastisch
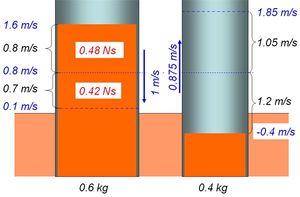
Der teilelastische oder reale Stoss liegt zwischen dem inelastischen und dem vollelastischen. Das Verhältnis zwischen der vom Impuls in der zweiten Phase aufgenommenen Energie zur vorher freigesetzten heisst Stosszahl. Weil die umgesetzte Energie proportional zum geflossenen Impuls und proportional zur Differenz der Anfangs- bzw. Endgeschwindigkeiten der beiden Körper ist, wächst der Energieumsatz quadratisch mit den Relativgeschwindigkeiten
- Stosszahl [math]\eta=\frac{W_{auf}}{W_{frei}}=\frac{(v_{nach}-v_{in})^2}{(v_{vor}-v_{in})^2}[/math]
Die Stosszahl ist für viele Materialien und in bestimmten Grenzen näherungsweise geschwindigkeitsunabhängig. Bei Güterwagen beträgt die Stosszahl etwa 0.33.
zentraler Stoss
Erhaltungsgrössen
Beim zentralen Stoss wird Impuls, aber kein Drehimpuls übertragen. Der zentrale Stoss kann auf den geraden Stoss zurückgeführt werden, indem z.B. die x-Achse des Koordinatensystems in Stossrichtung gelegt wird. Für die x-Komponente des Impulses gelten dann die Überlegungen des geraden Stosses. Die andern beiden Impuls-Komponenten werden nicht ausgetauscht und bleiben in den Stosspartnern drin.
Mathematisch kann der zentrale Stoss durch die Impulserhaltung beschrieben werden
- [math]\begin{pmatrix}p_{xtot}\\ p_{ytot}\\ p_{ztot}\end{pmatrix}=\begin{pmatrix}p_{x1v}\\p_{y1v}\\p_{z1v}\end{pmatrix}+\begin{pmatrix}p_{x2v} \\ p_{y2v}\\p_{z2v}\end{pmatrix}=\begin{pmatrix}p_{x1n}\\ p_{y1n}\\p_{z1n}\end{pmatrix}+\begin{pmatrix}p_{x2n}\\p_{y2n}\\ p_{z2n}\end{pmatrix}[/math]
Handelt es sich um einen elastischen Stoss, bleibt zusätzlich noch die kinetische Energie erhalten
- [math]W_{kin }=\frac{(\vec p_{1v})^2}{2m_1}+\frac{(\vec p_{2v})^2}{2m_2}=\frac{(\vec p_{1n})^2}{2m_1}+\frac{(\vec p_{2n})^2}{2m_2}[/math]
Massenmittelpunkt
Sind der Anfangsimpuls der beiden Stosspartner sowie die Massen gegeben, schränkt die Impulserhaltung den Endzustand bis auf drei unabhängige, skalare Grössen ein. Beobachtet man nun den Vorgang von einem System aus, das sich mit dem Massenmittelpunkt (MMP) bewegt, bleibt der Impuls der beiden Partner während des ganzen Stossvorganges gleich Null. In MMP-Bezugssystem sind die beiden Impulsvektoren zu jedem Zeitpunkt entgegengesetzt gleich gross (diese Betrachtungsweise entspricht im Flüssigkeitsbild dem Bezug der Geschwindigkeiten auf vin).
Der Betrag des Impulses der wegfliegenden Körper muss im MMP-System kleiner oder gleich wie der Betrag des Impulses der Körper vor dem Stoss sein, weil die kinetische Energie infolge Dissipation nur abnehmen kann. Im auf den MMP bezogenen Impulsraum bilden die Impulsvektoren der beiden aufeinander zufliegenden Körper den Durchmesser einer Kugel. Liegt der Impuls nachher auf der Kugeloberläche, ist der Stoss elastisch, anderfalls reichen die beiden Impulsvektoren nicht bis zur Kugeloberfläche.
schiefer Stoss
Beim schiefen Stoss wird Impuls und Drehimpuls übertragen. Der Name schief rührt von der Überlegung her, dass die Stosswirkung mit Hilfe einer Kraft ausgedrückt werden kann, deren Wirklinie schief zur Verbindungslinie der Massenmittelpunkte steht.
Mathematisch kann der schiefe Stoss durch die Impuls- und Drehimpulserhaltung beschrieben werden
- [math]\begin{pmatrix}p_{xtot}\\p_{ytot}\\p_{ztot}\end{pmatrix}=\begin{pmatrix}p_{x1v}\\p_{y1v}\\p_{z1v}\end{pmatrix}+\begin{pmatrix}p_{x2v}\\ p_{y2v}\\p_{z2v}\end{pmatrix}=\begin{pmatrix}p_{x1n}\\p_{y1n}\\p_{z1n}\end{pmatrix}+\begin{pmatrix}p_{x2n}\\p_{y2n}\\p_{z2n}\end{pmatrix}[/math]
- [math]\begin{pmatrix}L_{xtot}\\L_{ytot}\\L_{ztot}\end{pmatrix}=\begin{pmatrix}L_{x1v}\\L_{y1v}\\L_{z1v}\end{pmatrix}+\begin{pmatrix}L_{x2v}\\L_{y2v}\\L_{z2v}\end{pmatrix}=\begin{pmatrix}L_{x1n}\\ L_{y1n}\\L_{z1n}\end{pmatrix}+\begin{pmatrix}L_{x2n}\\ L_{y2n}\\L_{z2n}\end{pmatrix}[/math]
Die Bewegungsenergie bleibt beim schiefen Stoss in der Regel nicht erhalten, weil der gleichzeitige Austausch von Impuls und Drehimpuls meist dissipativ verläuft.
relativistischer Stoss
Nähert sich die Bewegung der Körper der Lichtgeschwindigkeit, machen sich die relativistischen Effekte bemerkbar. Energie (gleich Masse) und Impuls bilden dann gemeinsam einen vierdimensionalen Vektor in der Raum-Zeit. Um die vierte, die zeitliche Komponente dieses Vektors zu berechnen, multipliziert man die Masse mit der Lichtgeschwindigkeit oder dividiert die Gesamtenergie des Körpers mit der Lichtgeschwindigkeit
[math]p_T=m c=\frac {W}{c}[/math]
Stossen treffen Körper mit hoher Geschwindigkeit aufeinander, bleibt jede dieser vier Grössen erhalten
- [math]\begin{pmatrix}p_{Ttot}\\p_{xtot}\\p_{ytot}\\p_{ztot}\end{pmatrix}=\begin{pmatrix}p_{T1v}\\p_{x1v}\\p_{y1v}\\p_{z1v}\end{pmatrix}+\begin{pmatrix}p_{T2v}\\p_{x2v}\\p_{y2v}\\p_{z2v}\end{pmatrix}=\begin{pmatrix}p_{T1n}\\ p_{x1n}\\p_{y1n}\\ p_{z1n}\end{pmatrix}+\begin{pmatrix}p_{T2n} \\ p_{x2n}\\p_{y2n}\\p_{z2n}\end{pmatrix}[/math]
Elementarteilchen
Links
- unelastischer Stoss auf Youtube
- elastischer Stoss auf Youtube