Bilanzieren: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Admin (Diskussion | Beiträge) |
||
| (47 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Die klassische Physik kennt neben der [[Energie]] sieben [[Primärgrösse|bilanzierfähige Mengen]]. In dieser |
Die klassische Physik kennt neben der [[Energie]] sieben weitere [[Primärgrösse|bilanzierfähige Mengen]]. In dieser Vorlesung wird anhand der Grössen [[Masse]] und [[Volumen]] erklärt, was eine [[Bilanz]] ist und wie man eine Bilanz formuliert. Bilanzieren ([[System]] abgrenzen, Einflussgrössen identifizieren, Bilanz formulieren) gehört zu den grundlegenden Fähigkeiten eines gebildeten Menschen. Der praktische Nutzen des Bilanzierens reicht weit über die Physik hinaus. Ökonomen, Ingenieure, Naturwissenschafter, Ärzte und Politiker haben fast täglich mit Bilanzen zu tun. Ob Geld-, Material- oder Informationsflüsse quantitativ zu erfassen sind oder ein Medikament verabreicht werden muss, macht keinen grossen Unterschied. Ausgangspunkt ist immer das Bilanzieren. Parallel zu dieser Vorlesung werden Sie mit der [[System Dynamics|Systemdynamik]] vertraut gemacht, einer Modellbildungsmethode, welche das Bilanzieren massiv erleichtert. |
||
== Lernziele == |
== Lernziele == |
||
In dieser Vorlesung werden |
In dieser Vorlesung werden Sie lernen |
||
| ⚫ | |||
*wie eine Bilanz bezüglich eines Systems im allgemeinen Fall zu formulieren ist |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
*wie die Stärke eines [[Volumenstrom]]es mit der mittleren Strömungsgeschwindigkeit zusammenhängt |
*wie die Stärke eines [[Volumenstrom]]es mit der mittleren Strömungsgeschwindigkeit zusammenhängt |
||
*wie die [[Änderungsrate]] aus dem Inhalt berechnet wird |
*wie die [[Änderungsrate]] aus dem Inhalt berechnet wird |
||
| Zeile 25: | Zeile 24: | ||
Das Bundesamt für Umwelt übt Selbstkritik: «Jede Prognose ist mit einer Unsicherheit verbunden; wir haben gedacht, die Spitze käme später» , sagt Vizedirektor Andreas Götz. «Die Berner haben sich klar an die Regeln gehalten und sich auf die Prognose verlassen.» |
Das Bundesamt für Umwelt übt Selbstkritik: «Jede Prognose ist mit einer Unsicherheit verbunden; wir haben gedacht, die Spitze käme später» , sagt Vizedirektor Andreas Götz. «Die Berner haben sich klar an die Regeln gehalten und sich auf die Prognose verlassen.» |
||
Diese Pressemeldung lässt einige Fragen offen: |
|||
* |
*Hätten die Berner mit Hilfe des Bielersees den Aargau vor dem Hochwasser retten können? |
||
*Wie stark ist die "Murgenthaler Bedingung" verletzt worden? |
|||
*Welche Flüsse münden zwischen Bielersee und Murgenthal in die Aare? Wie viel Wasser haben diese Flüsse zusammen in die Aare eingeleitet? |
|||
*Wieso braucht es überhaupt eine Prognose? |
*Wieso braucht es überhaupt eine Prognose? |
||
*Wie modelliert man ein ganzes Flusssystem? |
|||
== Bilanz bezüglich des Bielersees == |
== Bilanz bezüglich des Bielersees == |
||
| Zeile 33: | Zeile 34: | ||
Der Bielersee weist ein Fläche von 39.3 km<sup>2</sup> auf, besitzt drei grössere Zuflüsse (Hagneck-Kanal, Schüss und Twannbach), ist mit dem Neuenburgersee über den Zihlkanal leitend verbunden und entwässert in den Nidau-Büren-Kanal. Gemessen werden die Volumenströme im Hagneck-, im Zihl- und im Nidau-Büren-Kanal sowie der Schüss (Suze) bei Sonceboz. |
Der Bielersee weist ein Fläche von 39.3 km<sup>2</sup> auf, besitzt drei grössere Zuflüsse (Hagneck-Kanal, Schüss und Twannbach), ist mit dem Neuenburgersee über den Zihlkanal leitend verbunden und entwässert in den Nidau-Büren-Kanal. Gemessen werden die Volumenströme im Hagneck-, im Zihl- und im Nidau-Büren-Kanal sowie der Schüss (Suze) bei Sonceboz. |
||
Damit sind das Bilanzgebiet und die grösseren Verbindungen mit der Umwelt festgelegt. Als bilanzierbare [[Menge]] nehmen wir die [[Masse]] des Wassers. Der Bielersee kann seinen Gehalt an Wasse |
Damit sind das Bilanzgebiet und die grösseren Verbindungen mit der Umwelt festgelegt. Als bilanzierbare [[Menge]] nehmen wir die [[Masse]] des Wassers. Der Bielersee kann seinen Gehalt an Wasse auf drei prinzipiell verschiedene Arten ändern |
||
*durch Zu- und Abstrom in Flüssen und Bächen |
*durch Zu- und Abstrom in Flüssen und Bächen |
||
*durch Regen, Verdunstung und Austausch mit dem Grundwasser |
*durch Regen, Verdunstung und Austausch mit dem Grundwasser |
||
*durch Vernichtung (Wasser kann chemisch gebunden werden) und Erzeugung (Wasser wird beim Abbau von organischem Material erzeugt) |
*durch Vernichtung (Wasser kann chemisch gebunden werden) und Erzeugung (Wasser wird beim Abbau von organischem Material erzeugt) |
||
Den Austausch über Flüsse und Bäche messen wir mit |
Den Austausch über Flüsse und Bäche messen wir mit der '''Massenstrom'''stärke ''I<sub>m</sub>'', den diffusen Austausch über die Oberfläche nennen wir '''Quelle''' und messen diese mit der Quellenstärke ''Σ<sub>m</sub>'', die Produktion von Wasser ist durch die '''Produktionsrate''' ''Π<sub>m</sub>'' bestimmt. Ein wegfliessender Massenstrom, eine Senke (z.B. durch Verdunstung) oder eine Vernichtung von Wasser auf chemischem Weg wird mit einem negativen Vorzeichen versehen. Strom- und Quellenstärken sowie Produktionsrate ändern den Inhalt des Bielersees. Die Änderung des Inhalts pro Zeit heisst [[Änderungsrate]]. Eine Änderungsrate ist demnach gleich der Inhaltsänderung dividiert durch die dazu benötigte Zeit. Die Änderungsrate der Masse wird mit einem Punkt über dem Formelzeichen (''m'') abgekürzt. |
||
Nun sind wir in der Lage, für den Bielersee eine saubere Massenbilanz zu formulieren: Die Summe über alle Stromstärken, die totale Quellenstärke und die totale Produktionsrate ergeben zu jedem Zeitpunkt die Änderungsrate |
Nun sind wir in der Lage, für den Bielersee eine saubere Massenbilanz zu formulieren: Die Summe über alle Stromstärken, die totale Quellenstärke und die totale Produktionsrate ergeben zu jedem Zeitpunkt die Änderungsrate im System. Dies lässt sich kompakt mit einer Formel schreiben |
||
:<math>\ |
:<math>\sum_i I_{m_i} + \Sigma_m + \Pi_m = \dot m</math> |
||
Merken Sie sich diese Bilanzgleichung in Worten und mit Formelzeichen. Sie gehört zu den wichtigsten Formeln der Physik. |
Merken Sie sich diese Bilanzgleichung in Worten und mit Formelzeichen. Sie gehört zu den wichtigsten Formeln der Physik. |
||
Statt der Masse kann auch das Volumen bilanziert werden. Der Zusammenhang zwischen der Massen- und der Volumenbilanz lässt sich am Beispiel der Stromstärke gut zeigen. |
Statt der [[Masse]] kann auch das [[Volumen]] bilanziert werden. Der Zusammenhang zwischen der Massen- und der Volumenbilanz lässt sich am Beispiel der Stromstärke gut zeigen. Die Dichte ist als Quotient von Masse durch Volumen definiert. Folglich ist die Masse gleich Dichte mal Volumen. Dieser Zusammenhang überträgt sich nun auch auf die Ströme: der Massenstrom ist gleich Dichte mal Volumenstrom (oft sagt man nur Strom, meint aber die Stromstärke) |
||
:<math>I_m = \ |
:<math>I_m = \varrho I_V</math> |
||
Die Volumenbilanz |
Die vereinfachte Volumenbilanz (ohne Quellenterm und Produktionsrate) lautet |
||
:<math>\ |
:<math>\sum_i I_{V_i} = \dot V</math> |
||
Die Summe über alle Volumenstromstärken ist gleich der Änderungsrate des Inhalts. Mit dieser Form der Volumenbilanz wollen wir nun weiter arbeiten. Alle Terme, die in einer Bilanzgleichung auftauchen, haben die Einheit Menge pro Zeit. In der Massenbilanz kommen demnach nur Grössen vor, die in Kilogramm pro Sekunde gemessen werden. Alle Grössen der Volumenbilanz |
'''Die Summe über alle Volumenstromstärken ist gleich der Änderungsrate des Inhalts'''. Mit dieser Form der Volumenbilanz wollen wir nun weiter arbeiten. Alle Terme, die in einer Bilanzgleichung auftauchen, haben die Einheit Menge pro Zeit. In der Massenbilanz kommen demnach nur Grössen vor, die in Kilogramm pro Sekunde gemessen werden. Alle Grössen der Volumenbilanz sind in m<sup>3</sup>/s anzugeben. |
||
== Volumenstrom und tranportiertes Volumen == |
== Volumenstrom und tranportiertes Volumen == |
||
[[Bild:Suze_Sonceboz.png|thumb|Volumenstrom der Schüss]] |
[[Bild:Suze_Sonceboz.png|thumb|Volumenstrom der Schüss]] |
||
Die Graphik zeigt, wie viel Wasser während der starken Regenfälle im August |
Die Graphik zeigt, wie viel Wasser während der starken Regenfälle im August 2007 durch die Suze bei Sonceboz geflossen sind. Etwas präziser formuliert, stellt die Graphik das [[Volumenstrom-Zeit-Diagramm]] der Suze bei Sonceboz dar. Wie viel Wasser ist nun aber in den drei Tagen vom Jura her in den Bielersee geflossen? |
||
Am Dienstag hat es wohl nur wenig geregnet. Die Schüss hat im Tagesmittel etwa 7 m<sup>3</sup>/s Wasser geführt. Multipliziert man diese Stromstärke mit der Zeit (86'400 s) sind am Dienstag, den 7. August 2007, etwa 600'000 m<sup>3</sup> Wasser von der Schüss durch Sonceboz transportiert worden. Das ist immerhin ein 60 Meter tiefer See mit einem Grundriss von 100 auf 100 Meter. |
Am Dienstag hat es wohl nur wenig geregnet. Die Schüss hat im Tagesmittel etwa 7 m<sup>3</sup>/s Wasser geführt. Multipliziert man diese Stromstärke mit der Zeit (86'400 s) sind am Dienstag, den 7. August 2007, etwa 600'000 m<sup>3</sup> Wasser von der Schüss durch Sonceboz transportiert worden. Das ist immerhin ein 60 Meter tiefer See mit einem Grundriss von 100 auf 100 Meter. |
||
| Zeile 64: | Zeile 65: | ||
Wie berechnet man nun die geflossene Wassermenge für Mittwoch, den 8. August 2007? Dafür gibt es mehrere Verfahren. Liegen die Messwerte in Form von Zahlenreihen vor (Volumenstrom und zugehörige Zeitpunkte), multipliziert man jeden Messwert für den Volumenstrom mit dem Zeitabschnitt, der vom jeweiligen Zeitpunkt bis zu dem des nächsten Messwerts reicht. Danach zählt man alle so berechneten Teilvolumen zusammen. Dieses Verfahren kann mit Hilfe von Excel oder Matlab blitzschnell ausgeführt werden. |
Wie berechnet man nun die geflossene Wassermenge für Mittwoch, den 8. August 2007? Dafür gibt es mehrere Verfahren. Liegen die Messwerte in Form von Zahlenreihen vor (Volumenstrom und zugehörige Zeitpunkte), multipliziert man jeden Messwert für den Volumenstrom mit dem Zeitabschnitt, der vom jeweiligen Zeitpunkt bis zu dem des nächsten Messwerts reicht. Danach zählt man alle so berechneten Teilvolumen zusammen. Dieses Verfahren kann mit Hilfe von Excel oder Matlab blitzschnell ausgeführt werden. |
||
Arbeitet man von Hand, wählt man einzelne Messwerte im Volumenstrom-Zeit-Diagramm aus und zieht von jedem Messpunkt eine horizontale Linie bis zum nächsten. Bei dieser "Treppenkonstruktion" nimmt man an, dass die Volumenstromstärke bis zum nächsten Messwert konstant bleibt. Nun entspricht das Produkt aus konstant gehaltenem Volumenstrom und Zeitabschnitt der Fläche unter der Stufe. Zählt man die Flächen unter allen Stufen zusammen, erhält man das total geflossene Volumen. Liegt eine dichte Folge von Messwerten vor, sind die Stufen nicht mehr erkennbar. Die Fläche unter allen Stufen nähert sich dann der effektiven '''Fläche unter der Kurve''' an. |
|||
Nun sind wir in der Lage, die Frage nach der in drei Tagen geflossenen Menge |
Nun sind wir in der Lage, die Frage nach der in drei Tagen geflossenen Menge mit wenig Aufwand zu beantworten. Dazu schätzen wir die Fläche unter der Kurve möglichst gut ab. Wieder sind mehrere Verfahren möglich. Am einfachsten unterteilt man die Kurve in ein paar wenige Stufen. Dabei ist darauf zu achten, dass das Rechteck unter der Stufe eine möglichst exakte Flächenverwandlung der ursprünglichen Kurve darstellt. Danach multipliziert man die Höhe der Stufe (mittlere Volumenstromstärke) mit der Länge der Stufe (Zeitabschnitt) und zählt alle so berechneten Teilvolumen zusammen. Die Suze hat demnach vom 8. August 0.00 Uhr bis zum 10. August 24.00 Uhr ..m<sup>3</sup> Wasser durch Sonceboz transportiert. |
||
Dieses Verfahren (aus einem beliebigen Stromstärke-Zeit-Diagramm die geflossene Menge ermitteln) müssen Sie so lange üben, bis Sie es für den Rest ihres Lebens können. Sie wissen dann z. B. auch, wie man aus einem [[zugeordneter Energiestrom|Energiestrom]]-Zeit-Diagramm die transportierte Energie ermittelt. |
|||
== Volumenstrom und Strömungsgeschwindigkeit == |
== Volumenstrom und Strömungsgeschwindigkeit == |
||
| Zeile 72: | Zeile 75: | ||
Der Hagneck-Kanal wurde als Teil der 1. Juragewässerkorrektion zwischen 1875 und 1878 gebaut, um die Aare in den Bielersee zu leiten. Mit den drei Seen als Ausgleichsbecken wollte man die Wassermenge im unteren Teil der Aare regeln und das Berner Seeland vor weiteren Überschwemmungen schützen. Bei der Mündung in den Bielersee ist 1900 ein Stauwehr errichtet worden, welches die 9 Meter Höhenunterschied zur Stromerzeugung ausnutzt. |
Der Hagneck-Kanal wurde als Teil der 1. Juragewässerkorrektion zwischen 1875 und 1878 gebaut, um die Aare in den Bielersee zu leiten. Mit den drei Seen als Ausgleichsbecken wollte man die Wassermenge im unteren Teil der Aare regeln und das Berner Seeland vor weiteren Überschwemmungen schützen. Bei der Mündung in den Bielersee ist 1900 ein Stauwehr errichtet worden, welches die 9 Meter Höhenunterschied zur Stromerzeugung ausnutzt. |
||
Das Diagramm zeigt unter anderem die Fliessgeschwindigkeit und den Volumenstrom. Man kann deutlich erkennen, dass bei Hochwasser der Volumenstrom stärker ansteigt als die Fliessgeschwindigkeit. Wie aus dem Pegelstand abzulesen ist, fliesst dann das Wasser durch einen grösseren |
Das Diagramm zeigt unter anderem die Fliessgeschwindigkeit und den Volumenstrom. Man kann deutlich erkennen, dass bei Hochwasser der Volumenstrom stärker ansteigt als die Fliessgeschwindigkeit. Wie aus dem Pegelstand abzulesen ist, fliesst dann das Wasser durch einen grösseren Querschnitt. Weil bei hohem Pegel bei gleicher Fliessgeschwindigkeit mehr Wasser durchgeführt wird als bei tiefem Pegelstand, steigt die Fliessgeschwindigkeit nicht so stark an wie die Volumenstromstärke. |
||
Der Zusammenhang zwischen Geschwindigkeit und Volumenstrom ist ziemlich kompliziert, weil die Strömung nicht überall gleich stark ist. Beschränkt man sich auf die mittlere Strömungsgeschwindigkeit, kann der Zusammenhang mittels einer einfachen Überlegung gefunden werden. Stellt man sich ein Prisma vor, das den Kanal auf einer bestimmten Länge vollständig ausfüllt, ist das zugehörige Volumen (''ΔV'') gleich Querschnitt (''A'') mal Länge des Prismas (''Δ s''). Bewegt sich nun das Prisma durch den Kanal, gilt für den Volumenstrom |
Der Zusammenhang zwischen Geschwindigkeit und Volumenstrom ist ziemlich kompliziert, weil die Strömung nicht überall gleich stark ist. Beschränkt man sich auf die mittlere Strömungsgeschwindigkeit, kann der Zusammenhang mittels einer einfachen Überlegung gefunden werden. Stellt man sich ein Prisma vor, das den Kanal auf einer bestimmten Länge vollständig ausfüllt, ist das zugehörige Volumen (''ΔV'') gleich Querschnitt (''A'') mal Länge des Prismas (''Δ s''). Bewegt sich nun das Prisma durch den Kanal, gilt für den Volumenstrom |
||
| Zeile 78: | Zeile 81: | ||
:<math>I_V = \frac {\Delta V}{\Delta t} = \frac {A \Delta s}{\Delta t} = A v</math> |
:<math>I_V = \frac {\Delta V}{\Delta t} = \frac {A \Delta s}{\Delta t} = A v</math> |
||
Die |
Die Volumenstromstärke ist gleich Querschnitt mal mittlere Strömungsgeschwindigkeit. Umgekehrt ist die mittlere Strömungsgeschwindigkeit als Volumenstromstärke durch Querschnitt definiert. |
||
Ist im nebenstehenden Diagramm mit Fliessgeschwindigkeit die mittleren Strömungsgeschwindigkeit gemeint, kann der wasserführende Querschnitt des Hagneck-Kanals berechnet werden. Am Mittwoch morgen, den 8. August 2007, betrug dieser Querschnitt etwa 230 m<sup>2</sup>. Am Donnerstag ist der Wasser führende Querschnitt auf etwa 270 m<sup>2</sup> angewachsen. Weil gleichzeitig der Pegel um 2.2 m gestiegen ist, kann die Breite des Hagneck-Kanals auf etwa 18 m geschätzt werden. |
|||
== Inhalt und Änderungsrate == |
== Inhalt und Änderungsrate == |
||
[[Bild:Bielersee_h.png|thumb|Pegelstand des Bielersees]] |
[[Bild:Bielersee_h.png|thumb|Pegelstand des Bielersees]] |
||
Die Zu- und Abflüsse verändern den Inhalt eines Systems: die Summe über die Stärken der Volumenströme und |
Die Zu- und Abflüsse verändern den Inhalt eines Systems: die Summe über die Stärken der Volumenströme und Volumenquellen plus die Produktionsrate sind gleich der [[Änderungsrate]] des Volumens. Beim Wasservolumen ist Produktionsrate infolge Kompression sehr klein und kann vernachlässigt werden. Kennt man die Volumenströme und die Quellenstärke (Regen, Verdunstung), ist die Volumenänderungsrate über die Bilanzgleichung berechenbar. Doch wie ermittelt man die Änderungsrate, wenn das Volumen in Funktion der Zeit gegeben ist? |
||
Die Änderungsrate ist als Inhaltsänderung pro Zeit definiert. Kennt man den Inhalt zu zwei verschiedenen Zeitpunkten, ist die mittlere Änderungsrate im Zeitabschnitt ''Δ t'' (Differenz der beiden Zeitpunkte) definiert als |
|||
:<math>\dot V_{mittel} = \frac {V_2 - V_1}{t_2 - t_1} = \frac {\Delta V}{\Delta t}</math> |
:<math>\dot V_{mittel} = \frac {V_2 - V_1}{t_2 - t_1} = \frac {\Delta V}{\Delta t}</math> |
||
Gemäss dieser Definition wird die Änderungsrate automatisch negativ, sobald der Inhalt abnimmt. |
|||
Weil beim Bielersee bloss der Pegelstand (die Höhe über Meer) gemessen werden, müssen wir noch eine Zusatzüberlegung machen. Ändert sich die Fläche des Sees mit der Füllhöhe nicht allzu stark, darf der veränderliche Teil des Seevolumens als Prisma modelliert werden. Die Volumenänderung ist dann gleich Seefläche ''A'' mal Zu- oder Abnahme der Höhe (''Δ h''). Daraus folgt |
|||
:<math>\dot V_{mittel} = \frac {A \Delta h}{\Delta t} = A \dot h_{mittel}</math> |
:<math>\dot V_{mittel} = \frac {A \Delta h}{\Delta t} = A \dot h_{mittel}</math> |
||
Nun ist die Höhenänderungsrate die Geschwindigkeit, mit welcher der Seespiegel steigt oder fällt. Damit ist die Volumenänderungsrate bei prismatischen Gefässen gleich Grundfläche mal Geschwindigkeit des Flüssigkeitsspiegels. Diese Formel entspricht exakt dem Zusammenhang zwischen Volumenstromstärke und Strömungsgeschwindigkeit. Merken Sie sich also den folgenden Zusammenhang: |
|||
:'''Die Volumenänderungsrate ist gleich Grundfläche mal Geschwindigkeit des Seespiegels''' |
|||
| ⚫ | Liegt der Pegelstand in Funktion der Zeit als |
||
| ⚫ | Liegt der Pegelstand in Funktion der Zeit als graphische Darstellung vor (Höhen-Zeit-Diagramm), kann man zwei Punkte herauslesen und den Quotienten aus Höhenänderung und zugehörigem Zeitabschnitt bilden. Dieser Quotient beschreibt - bildlich gesprochen - die Steigung einer Geraden durch die beiden ausgewählten Punkte (Steigung der Sekante). Verschiebt man nun den einen Punkt gegen den andern, geht die [https://de.wikipedia.org/wiki/Sekante Sekante] in die [https://de.wikipedia.org/wiki/Tangente Tangente] des festgehaltenen Punktes über. Die Tangentenkonstruktion (Punkt auswählen, Tangente an die Kurve legen, Steigung bestimmen) erlaubt es uns, aus einem beliebigen Pegelstand-Zeit-Diagramm die Steig- oder Sinkgeschwindigkeit zu bestimmen. Mit diesem Verfahren kann aber auch aus jedem [[Orts-Zeit-Diagramm]] (fälschlicherweise oft Weg-Zeit-Diagramm genannt) die Geschwindigkeit ermittelt werden. |
||
Liegt direkt ein Volumen-Zeit-Diagramm vor, gilt der analoge Zusammenhang. Um die Änderungsrate zu einem bestimmten Zeitpunkt zu bestimmen, zeichnet man die Tangente an die Kurve. Die zugehörige Steigung (Voumenänderung längs der Tangente durch benötigte Zeit) entspricht der momentanen Volumenänderungsrate. |
|||
Üben Sie dieses Verfahren an den Beispielen Volumen-Zeit-Diagramm und Orts-Zeit-Diagramm so lange, bis Sie es im Traum beherrschen. Sie wissen dann auch, wie man aus einem Geschwindigkeits-Zeit-Diagramm die Beschleunigung ermittelt, falls Sie das in der Mittelschule noch nie gehört haben. |
|||
== Volumenbilanz == |
== Volumenbilanz == |
||
[[Bild:Zihlkanal.png|thumb|Volumenstrom und Pegelstand im Zihlkanal]] |
|||
Die Graphik zeigt den Volumenstrom im Zihlkanal. In dieser Verbindung zwischen dem Neuenburger und Bielersee kann das Wasser je nach Pegelstände in beide Richtungen strömen. Fliesst eine [[Menge]] wechselseitig durch einen Leitungsabschnitt, muss das Vorzeichen der Stromstärke festgelegt werden. Dazu führt man einen [[Bezugspfeil]] längs der Leitung ein. Das Vorzeichen der Stromstärke bezüglich des Pfeils überträgt sich auf die Bilanz bezüglich des Speichers, auf den der Pfeil zeigt. Bezüglich des Speichers am andern Ende der Leitung ist die gleiche Stromstärke mit dem entgegengesetzten Vorzeichen zu bilanzieren. Beim Zihlkanal wird ein Strom, der vom Neuenburger zum Bielersee fliesst, positiv gezählt. Fliesst nun das Wasser wie am 10. August 2007 vom Bielersee in den Neuenburgersee, hat der Volumenstrom eine negative Stärke. Dieser Wert wird in der Volumenbilanz bezüglich des Bielersees direkt und in die Bilanz bezüglich des Neuenburgersees mit umgekehrtem Vorzeichen verrechnet. Die [[System Dynamics|systemdynamischen Modellierungstools]] wenden die Vorzeichenregel genau so an. Zeigt eine Flussgrösse (Pipeline) in die Bestandesgrösse (Topf) hinein, wird eine gegebene Stromstärke direkt in die Bilanz eingefügt. Zeigt die Flussgrösse hinaus, wird in der Bilanz die zugehörige Stromstärke subtrahiert. |
|||
Nun wollen wir die Bilanz bezüglich des Bielersees zum Zeitpunkt 8. August 2007 24 Uhr auswerten. Zu diesem Zeitpunt strömten durch den Hagneckkanal 1170 m<sup>3</sup>/s in den Bielersee hinein, die Schüss brachte zusätzlich 45 m<sup>3</sup>/s und aus dem Ziehlkanal flossen 140 m<sup>3</sup>/s gegen den Neuenburgersee. Der Pegel des Bilersees stieg mit einer Geschwindigkeit von 1.9 10<sup>-5</sup> m/s, was auf den ganzen See hochgerechnet eine Änderungsrate von 760 m<sup>3</sup>/s ergibt. Folglich mussten 315 m<sup>3</sup>/s über den Nidau-Büren-Kanal abgeflossen sein. Die Messstelle in Brügg hat einen Wert von 280 m<sup>3</sup>/s festgestellt. Wie können wir die Differenz erklären? |
|||
Drei Gründe für diesen Unterschied zwischen theoretischer Vorhersagen (Bilanzgleichung) und der Messung können geltend gemacht werden: |
|||
#weitere Zuflüsse und Quellenterme (Dauerregen) |
|||
#Grösse des Sees (kein homogenes System, Wind kann den Seespiegel verformen) |
|||
#Laufzeit der Flutwelle |
|||
Wie stark diese Störterme die Bilanz beeinflussen, ist schwer abzuschätzen. Die folgenden Bemerkungen sollen Hinweise für eine erste Beurteilung liefern |
|||
#In den Bielersee fliessen einige Bäche. Dazu kommt noch das Oberflächenwasser der Umgebung. Insgesamt dürfte dies alles zusammen kaum mehr als die Suze ausmachen. Ein kräftiger Regen kann 10 bis 50 mm Niederschlag pro Stunde bringen. Geht man von 20 mm aus, gibt das auf den Bielersee hochgerechnet etwa 220 m<sup>3</sup>/s. Die Wirkung der Bäche und des Oberflächenwassers auf die Bilanz könnte mit einer grösseren Fläche bei der Berechnung der Regenmenge berücksichtigt werden. |
|||
#Der Pegel wird bei Ligerz gemessen. Weil die Seeoberfläche durch den Wind bewegt werden kann, müsste man an mehreren Stellen des Sees den Pegelstand ermitteln. |
|||
#Ergiesst sich plötzlich ein starker Strom in den See, dauert es eine gewisse Zeit, bis sich dieses Wasser auf den ganzen See verteilt hat. Zudem müsste man noch wissen, wie weit die Messstelle Brügg vom Ausfluss aus dem Bielersee entfernt ist. Je weiter flussabwärts eine Messstelle gelegen ist, umso länger dauert es, bis sich dort eine Änderung der Stromstärke bemerkbar macht. |
|||
== Modellbildung == |
== Modellbildung == |
||
[[Bild:Aare_Bruegg.png|thumb|Volumenstrom der Aare bei Brügg]] |
|||
Durch den Nidau-Büren-Kanal sind in der kritischen Phase maximal 500 m<sup>3</sup>/s geflossen. Dieser Strom hätte die "Murgenthaler-Bedingung" nicht verletzen können. Andere Flüsse haben das ihre beigetragen. So hat in der fraglichen Nacht allein die Emme 600 m<sup>3</sup>/s in die Aare eingebracht. Die Idee wäre aber gewesen, dass man den Ausfluss aus dem Bielersee so weit drosselt, dass trotz der Emme und ein paar weiterer Flüssen die "Murgenthaler-Bedingung" erfüllt geblieben wäre. Weil alle diese Wassermengen eine gewisse Zeit brauchen, bis sie den Kanton Aargau erreichen, muss man das ganze hydraulische System der Aare und ihrer Zuflüsse in ein Simulationsmodell abbilden. |
|||
Modelle ganzer Flusssysteme sind - wie das Beispiel zeigt - nicht einfach zu erstellen. Das ist Aufgabe der Spezialisten. Sie werden in diesem Kurs aber lernen, wie man Modelle einfacher Systeme (homogen, wenige [[Zustandsgrösse]]n) baut, wie man die Simulationsergebnisse mit Messungen vergleicht und wie man ein Modell an die Messdaten anpasst. |
|||
== Kontrollfragen == |
|||
#Formulieren Sie die Volumenbilanz bezüglich des Bielersees. |
|||
#Am 30. August 2007 hat der Rhein 2400 m<sup>3</sup> Wasser pro Sekunde durch Basel transportiert. Wie schnell wäre das Wasser im Mittel geflossen, wenn der Rheins dort einen rechteckigen Querschnitt von 200 m auf 3 m hätte? |
|||
#Welchen Wert hat die Volumenänderungsrate des Bielersees am 9. August 2007 im Mittel angenommen? |
|||
#Wie viel Wasser ist am 9. August 2007 durch den Hagneck-Kanal in den Bieldersee geflossen? |
|||
#Um wie viel wäre der Bielersee an diesem Tag gestiegen, wenn keine weiteren Zu- und Abflüsse vorhanden gewesen wären? |
|||
==Antworten zu den Kontrollfragen== |
|||
#Die Summe über die Volumenstromstärken von Schüss, Twannbach, Hagneck-, Zihl- und Nidau-Büren-Kanal ist gleich der Volumenänderungsrate des Bielersees. In dieser Bilanz sind die Beiträge der kleinen Bäche, des Oberflächenwassers, des Regens und der Verdunstung nicht aufgeführt. Die Vernichtung und Erzeugung von Wasser durch chemische und biologische Aktivitäten fallen kaum ins Gewicht. |
|||
#Die mittlere Strömungsgeschwindigkeit ist definiert als Quotient aus Volumenstrom und Querschnitt: <math>\overline v=\frac{I_V}{A}</math> = 4 m/s. |
|||
#Am 9. August 2007 ist der Spiegel des Bielersees von 429.85 m auf 430.9 m gestiegen. Multipliziert man diesen Höhenunterschied von 1.05 m mit der Fläche des Sees (39.3 km<sup>2</sup>), erhält man die gesamte Volumenänderung. Eine Division durch 86400 s liefert danach den gesuchten Wert von etwa 480 m<sup>3</sup>/s. |
|||
#Am 9. August 2007 strömten im Mittel etwa 1200 m<sup>3</sup>/s durch den Hagneck-Kanal. Multipliziert man diesen Wert mit 86400 s, erhält 1.04*10<sup>8</sup> m<sup>3</sup> oder 0.104 km<sup>3</sup> Wasser. |
|||
#Wäre nur Wasser durch den Hagneck-Kanal zugeflossen, hätte sich der Spiegel des Bieldersees um etwa <math>\Delta h=\frac{\Delta V}{A}</math> = 2.6 m gehoben. |
|||
== Materialien == |
|||
*[https://home.zhaw.ch/~mau/Lehre/Skript/HydraulikT.pdf Skript] Seite 1 |
|||
*[[Physik - Ein systemdynamischer Zugang für die Sekundarstufe II]] Seiten 23 - 33 |
|||
*[http://www.pegaswiss.ch/Hydrodynamik/index.php eLearning] Teilmodule Einführung und Volumenbilanz |
|||
*[https://cast.switch.ch/vod/clips/1e01ayxfqs/link_box Videoaufzeichnung] |
|||
*[http://www.youtube.com/watch?v=pfaPep6-4po Kurzfassung auf Yotube] |
|||
'''[[Physik und Systemwissenschaft in Aviatik 2014]]''' |
|||
'''[[Physik und Systemwissenschaft in Aviatik]]''' |
|||
[[Kategorie:VorAV]] |
|||
Aktuelle Version vom 15. September 2015, 08:05 Uhr
Die klassische Physik kennt neben der Energie sieben weitere bilanzierfähige Mengen. In dieser Vorlesung wird anhand der Grössen Masse und Volumen erklärt, was eine Bilanz ist und wie man eine Bilanz formuliert. Bilanzieren (System abgrenzen, Einflussgrössen identifizieren, Bilanz formulieren) gehört zu den grundlegenden Fähigkeiten eines gebildeten Menschen. Der praktische Nutzen des Bilanzierens reicht weit über die Physik hinaus. Ökonomen, Ingenieure, Naturwissenschafter, Ärzte und Politiker haben fast täglich mit Bilanzen zu tun. Ob Geld-, Material- oder Informationsflüsse quantitativ zu erfassen sind oder ein Medikament verabreicht werden muss, macht keinen grossen Unterschied. Ausgangspunkt ist immer das Bilanzieren. Parallel zu dieser Vorlesung werden Sie mit der Systemdynamik vertraut gemacht, einer Modellbildungsmethode, welche das Bilanzieren massiv erleichtert.
Lernziele
In dieser Vorlesung werden Sie lernen
- wie eine Volumenbilanz oder Massenbilanz formuliert wird
- wie aus dem Volumenstrom-Zeit-Diagramm das geflossene Volumen berechnet wird
- wie die Stärke eines Volumenstromes mit der mittleren Strömungsgeschwindigkeit zusammenhängt
- wie die Änderungsrate aus dem Inhalt berechnet wird
- wie aus dem Füllhöhen-Zeit-Diagramm die Volumenänderungsrate bestimmt wird
Problemstellung
10. August 2007, 19:18; Letzte Aktualisierung: 20:43; Quelle: sf drs
Berner liessen die Aargauer untergehen/Schleusen im Bielersee zu stark offen
Der Kanton Aargau wurde besonders stark von den Überschwemmungen getroffen. Mitverantwortlich ist der Kanton Bern, der die Schleusen beim Bielersee zu stark geöffnet hatte. Das Bundesamt für Umwelt nimmt die Berner in Schutz.
Der Aargauer Gewässerkenner Pierre-Yves Christen rieb sich am Donnerstag die Augen, als er die unglaublichen Zahlen sah: Die Aare floss mit knapp 1300 Kubikmetern pro Sekunde durch Murgenthal (AG) – viel mehr als erlaubt. Denn laut «Murgenthaler Bedingung» darf die Aare bei Murgenthal nicht mehr als 850 Kubikmeter Wasser pro Sekunde führen. Offensichtlich hatte der Kanton Bern die Schleusen am bedrohlich steigenden Bielersee zu stark geöffnet, wie die «Aargauer Zeitung» mutmasste.
Tatsächlich waren die Schleusen in Biel nach Informationen von SF Tagesschau für lange Zeit zu weit offen. Der Kanton Bern hatte sich auf eine Prognose des Bundes gestützt, die den Höchststand des Wassers erst für Donnerstag Vormittag vorsah. Die Wassermassen waren jedoch schneller und die Schleusen konnten nicht mehr rechtzeitig geschlossen werden.
Das Bundesamt für Umwelt übt Selbstkritik: «Jede Prognose ist mit einer Unsicherheit verbunden; wir haben gedacht, die Spitze käme später» , sagt Vizedirektor Andreas Götz. «Die Berner haben sich klar an die Regeln gehalten und sich auf die Prognose verlassen.»
Diese Pressemeldung lässt einige Fragen offen:
- Hätten die Berner mit Hilfe des Bielersees den Aargau vor dem Hochwasser retten können?
- Welche Flüsse münden zwischen Bielersee und Murgenthal in die Aare? Wie viel Wasser haben diese Flüsse zusammen in die Aare eingeleitet?
- Wieso braucht es überhaupt eine Prognose?
- Wie modelliert man ein ganzes Flusssystem?
Bilanz bezüglich des Bielersees
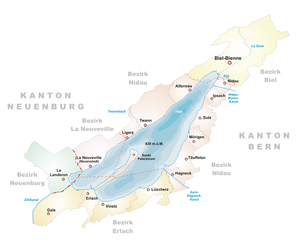
Der Bielersee weist ein Fläche von 39.3 km2 auf, besitzt drei grössere Zuflüsse (Hagneck-Kanal, Schüss und Twannbach), ist mit dem Neuenburgersee über den Zihlkanal leitend verbunden und entwässert in den Nidau-Büren-Kanal. Gemessen werden die Volumenströme im Hagneck-, im Zihl- und im Nidau-Büren-Kanal sowie der Schüss (Suze) bei Sonceboz.
Damit sind das Bilanzgebiet und die grösseren Verbindungen mit der Umwelt festgelegt. Als bilanzierbare Menge nehmen wir die Masse des Wassers. Der Bielersee kann seinen Gehalt an Wasse auf drei prinzipiell verschiedene Arten ändern
- durch Zu- und Abstrom in Flüssen und Bächen
- durch Regen, Verdunstung und Austausch mit dem Grundwasser
- durch Vernichtung (Wasser kann chemisch gebunden werden) und Erzeugung (Wasser wird beim Abbau von organischem Material erzeugt)
Den Austausch über Flüsse und Bäche messen wir mit der Massenstromstärke Im, den diffusen Austausch über die Oberfläche nennen wir Quelle und messen diese mit der Quellenstärke Σm, die Produktion von Wasser ist durch die Produktionsrate Πm bestimmt. Ein wegfliessender Massenstrom, eine Senke (z.B. durch Verdunstung) oder eine Vernichtung von Wasser auf chemischem Weg wird mit einem negativen Vorzeichen versehen. Strom- und Quellenstärken sowie Produktionsrate ändern den Inhalt des Bielersees. Die Änderung des Inhalts pro Zeit heisst Änderungsrate. Eine Änderungsrate ist demnach gleich der Inhaltsänderung dividiert durch die dazu benötigte Zeit. Die Änderungsrate der Masse wird mit einem Punkt über dem Formelzeichen (m) abgekürzt.
Nun sind wir in der Lage, für den Bielersee eine saubere Massenbilanz zu formulieren: Die Summe über alle Stromstärken, die totale Quellenstärke und die totale Produktionsrate ergeben zu jedem Zeitpunkt die Änderungsrate im System. Dies lässt sich kompakt mit einer Formel schreiben
- [math]\sum_i I_{m_i} + \Sigma_m + \Pi_m = \dot m[/math]
Merken Sie sich diese Bilanzgleichung in Worten und mit Formelzeichen. Sie gehört zu den wichtigsten Formeln der Physik.
Statt der Masse kann auch das Volumen bilanziert werden. Der Zusammenhang zwischen der Massen- und der Volumenbilanz lässt sich am Beispiel der Stromstärke gut zeigen. Die Dichte ist als Quotient von Masse durch Volumen definiert. Folglich ist die Masse gleich Dichte mal Volumen. Dieser Zusammenhang überträgt sich nun auch auf die Ströme: der Massenstrom ist gleich Dichte mal Volumenstrom (oft sagt man nur Strom, meint aber die Stromstärke)
- [math]I_m = \varrho I_V[/math]
Die vereinfachte Volumenbilanz (ohne Quellenterm und Produktionsrate) lautet
- [math]\sum_i I_{V_i} = \dot V[/math]
Die Summe über alle Volumenstromstärken ist gleich der Änderungsrate des Inhalts. Mit dieser Form der Volumenbilanz wollen wir nun weiter arbeiten. Alle Terme, die in einer Bilanzgleichung auftauchen, haben die Einheit Menge pro Zeit. In der Massenbilanz kommen demnach nur Grössen vor, die in Kilogramm pro Sekunde gemessen werden. Alle Grössen der Volumenbilanz sind in m3/s anzugeben.
Volumenstrom und tranportiertes Volumen
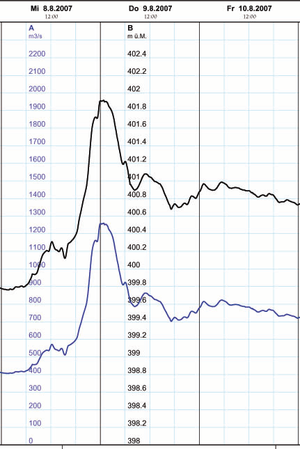
Die Graphik zeigt, wie viel Wasser während der starken Regenfälle im August 2007 durch die Suze bei Sonceboz geflossen sind. Etwas präziser formuliert, stellt die Graphik das Volumenstrom-Zeit-Diagramm der Suze bei Sonceboz dar. Wie viel Wasser ist nun aber in den drei Tagen vom Jura her in den Bielersee geflossen?
Am Dienstag hat es wohl nur wenig geregnet. Die Schüss hat im Tagesmittel etwa 7 m3/s Wasser geführt. Multipliziert man diese Stromstärke mit der Zeit (86'400 s) sind am Dienstag, den 7. August 2007, etwa 600'000 m3 Wasser von der Schüss durch Sonceboz transportiert worden. Das ist immerhin ein 60 Meter tiefer See mit einem Grundriss von 100 auf 100 Meter.
Wie berechnet man nun die geflossene Wassermenge für Mittwoch, den 8. August 2007? Dafür gibt es mehrere Verfahren. Liegen die Messwerte in Form von Zahlenreihen vor (Volumenstrom und zugehörige Zeitpunkte), multipliziert man jeden Messwert für den Volumenstrom mit dem Zeitabschnitt, der vom jeweiligen Zeitpunkt bis zu dem des nächsten Messwerts reicht. Danach zählt man alle so berechneten Teilvolumen zusammen. Dieses Verfahren kann mit Hilfe von Excel oder Matlab blitzschnell ausgeführt werden.
Arbeitet man von Hand, wählt man einzelne Messwerte im Volumenstrom-Zeit-Diagramm aus und zieht von jedem Messpunkt eine horizontale Linie bis zum nächsten. Bei dieser "Treppenkonstruktion" nimmt man an, dass die Volumenstromstärke bis zum nächsten Messwert konstant bleibt. Nun entspricht das Produkt aus konstant gehaltenem Volumenstrom und Zeitabschnitt der Fläche unter der Stufe. Zählt man die Flächen unter allen Stufen zusammen, erhält man das total geflossene Volumen. Liegt eine dichte Folge von Messwerten vor, sind die Stufen nicht mehr erkennbar. Die Fläche unter allen Stufen nähert sich dann der effektiven Fläche unter der Kurve an.
Nun sind wir in der Lage, die Frage nach der in drei Tagen geflossenen Menge mit wenig Aufwand zu beantworten. Dazu schätzen wir die Fläche unter der Kurve möglichst gut ab. Wieder sind mehrere Verfahren möglich. Am einfachsten unterteilt man die Kurve in ein paar wenige Stufen. Dabei ist darauf zu achten, dass das Rechteck unter der Stufe eine möglichst exakte Flächenverwandlung der ursprünglichen Kurve darstellt. Danach multipliziert man die Höhe der Stufe (mittlere Volumenstromstärke) mit der Länge der Stufe (Zeitabschnitt) und zählt alle so berechneten Teilvolumen zusammen. Die Suze hat demnach vom 8. August 0.00 Uhr bis zum 10. August 24.00 Uhr ..m3 Wasser durch Sonceboz transportiert.
Dieses Verfahren (aus einem beliebigen Stromstärke-Zeit-Diagramm die geflossene Menge ermitteln) müssen Sie so lange üben, bis Sie es für den Rest ihres Lebens können. Sie wissen dann z. B. auch, wie man aus einem Energiestrom-Zeit-Diagramm die transportierte Energie ermittelt.
Volumenstrom und Strömungsgeschwindigkeit
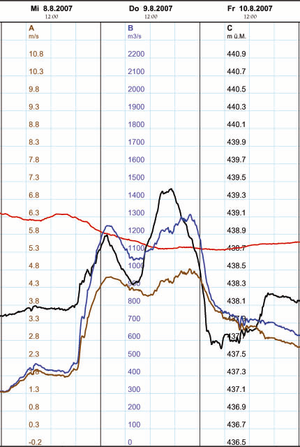
Der Hagneck-Kanal wurde als Teil der 1. Juragewässerkorrektion zwischen 1875 und 1878 gebaut, um die Aare in den Bielersee zu leiten. Mit den drei Seen als Ausgleichsbecken wollte man die Wassermenge im unteren Teil der Aare regeln und das Berner Seeland vor weiteren Überschwemmungen schützen. Bei der Mündung in den Bielersee ist 1900 ein Stauwehr errichtet worden, welches die 9 Meter Höhenunterschied zur Stromerzeugung ausnutzt.
Das Diagramm zeigt unter anderem die Fliessgeschwindigkeit und den Volumenstrom. Man kann deutlich erkennen, dass bei Hochwasser der Volumenstrom stärker ansteigt als die Fliessgeschwindigkeit. Wie aus dem Pegelstand abzulesen ist, fliesst dann das Wasser durch einen grösseren Querschnitt. Weil bei hohem Pegel bei gleicher Fliessgeschwindigkeit mehr Wasser durchgeführt wird als bei tiefem Pegelstand, steigt die Fliessgeschwindigkeit nicht so stark an wie die Volumenstromstärke.
Der Zusammenhang zwischen Geschwindigkeit und Volumenstrom ist ziemlich kompliziert, weil die Strömung nicht überall gleich stark ist. Beschränkt man sich auf die mittlere Strömungsgeschwindigkeit, kann der Zusammenhang mittels einer einfachen Überlegung gefunden werden. Stellt man sich ein Prisma vor, das den Kanal auf einer bestimmten Länge vollständig ausfüllt, ist das zugehörige Volumen (ΔV) gleich Querschnitt (A) mal Länge des Prismas (Δ s). Bewegt sich nun das Prisma durch den Kanal, gilt für den Volumenstrom
- [math]I_V = \frac {\Delta V}{\Delta t} = \frac {A \Delta s}{\Delta t} = A v[/math]
Die Volumenstromstärke ist gleich Querschnitt mal mittlere Strömungsgeschwindigkeit. Umgekehrt ist die mittlere Strömungsgeschwindigkeit als Volumenstromstärke durch Querschnitt definiert.
Ist im nebenstehenden Diagramm mit Fliessgeschwindigkeit die mittleren Strömungsgeschwindigkeit gemeint, kann der wasserführende Querschnitt des Hagneck-Kanals berechnet werden. Am Mittwoch morgen, den 8. August 2007, betrug dieser Querschnitt etwa 230 m2. Am Donnerstag ist der Wasser führende Querschnitt auf etwa 270 m2 angewachsen. Weil gleichzeitig der Pegel um 2.2 m gestiegen ist, kann die Breite des Hagneck-Kanals auf etwa 18 m geschätzt werden.
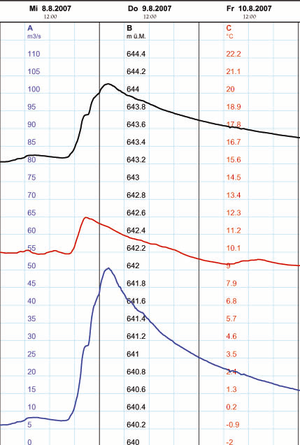
Inhalt und Änderungsrate
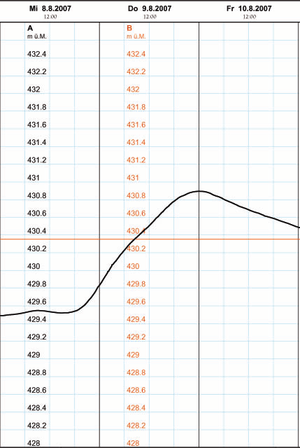
Die Zu- und Abflüsse verändern den Inhalt eines Systems: die Summe über die Stärken der Volumenströme und Volumenquellen plus die Produktionsrate sind gleich der Änderungsrate des Volumens. Beim Wasservolumen ist Produktionsrate infolge Kompression sehr klein und kann vernachlässigt werden. Kennt man die Volumenströme und die Quellenstärke (Regen, Verdunstung), ist die Volumenänderungsrate über die Bilanzgleichung berechenbar. Doch wie ermittelt man die Änderungsrate, wenn das Volumen in Funktion der Zeit gegeben ist?
Die Änderungsrate ist als Inhaltsänderung pro Zeit definiert. Kennt man den Inhalt zu zwei verschiedenen Zeitpunkten, ist die mittlere Änderungsrate im Zeitabschnitt Δ t (Differenz der beiden Zeitpunkte) definiert als
- [math]\dot V_{mittel} = \frac {V_2 - V_1}{t_2 - t_1} = \frac {\Delta V}{\Delta t}[/math]
Gemäss dieser Definition wird die Änderungsrate automatisch negativ, sobald der Inhalt abnimmt.
Weil beim Bielersee bloss der Pegelstand (die Höhe über Meer) gemessen werden, müssen wir noch eine Zusatzüberlegung machen. Ändert sich die Fläche des Sees mit der Füllhöhe nicht allzu stark, darf der veränderliche Teil des Seevolumens als Prisma modelliert werden. Die Volumenänderung ist dann gleich Seefläche A mal Zu- oder Abnahme der Höhe (Δ h). Daraus folgt
- [math]\dot V_{mittel} = \frac {A \Delta h}{\Delta t} = A \dot h_{mittel}[/math]
Nun ist die Höhenänderungsrate die Geschwindigkeit, mit welcher der Seespiegel steigt oder fällt. Damit ist die Volumenänderungsrate bei prismatischen Gefässen gleich Grundfläche mal Geschwindigkeit des Flüssigkeitsspiegels. Diese Formel entspricht exakt dem Zusammenhang zwischen Volumenstromstärke und Strömungsgeschwindigkeit. Merken Sie sich also den folgenden Zusammenhang:
- Die Volumenänderungsrate ist gleich Grundfläche mal Geschwindigkeit des Seespiegels
Liegt der Pegelstand in Funktion der Zeit als graphische Darstellung vor (Höhen-Zeit-Diagramm), kann man zwei Punkte herauslesen und den Quotienten aus Höhenänderung und zugehörigem Zeitabschnitt bilden. Dieser Quotient beschreibt - bildlich gesprochen - die Steigung einer Geraden durch die beiden ausgewählten Punkte (Steigung der Sekante). Verschiebt man nun den einen Punkt gegen den andern, geht die Sekante in die Tangente des festgehaltenen Punktes über. Die Tangentenkonstruktion (Punkt auswählen, Tangente an die Kurve legen, Steigung bestimmen) erlaubt es uns, aus einem beliebigen Pegelstand-Zeit-Diagramm die Steig- oder Sinkgeschwindigkeit zu bestimmen. Mit diesem Verfahren kann aber auch aus jedem Orts-Zeit-Diagramm (fälschlicherweise oft Weg-Zeit-Diagramm genannt) die Geschwindigkeit ermittelt werden.
Liegt direkt ein Volumen-Zeit-Diagramm vor, gilt der analoge Zusammenhang. Um die Änderungsrate zu einem bestimmten Zeitpunkt zu bestimmen, zeichnet man die Tangente an die Kurve. Die zugehörige Steigung (Voumenänderung längs der Tangente durch benötigte Zeit) entspricht der momentanen Volumenänderungsrate.
Üben Sie dieses Verfahren an den Beispielen Volumen-Zeit-Diagramm und Orts-Zeit-Diagramm so lange, bis Sie es im Traum beherrschen. Sie wissen dann auch, wie man aus einem Geschwindigkeits-Zeit-Diagramm die Beschleunigung ermittelt, falls Sie das in der Mittelschule noch nie gehört haben.
Volumenbilanz
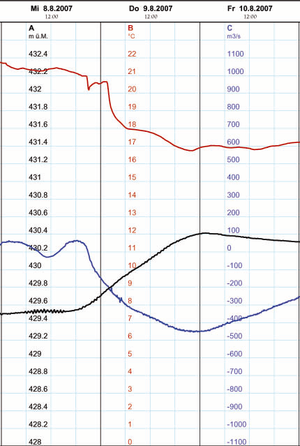
Die Graphik zeigt den Volumenstrom im Zihlkanal. In dieser Verbindung zwischen dem Neuenburger und Bielersee kann das Wasser je nach Pegelstände in beide Richtungen strömen. Fliesst eine Menge wechselseitig durch einen Leitungsabschnitt, muss das Vorzeichen der Stromstärke festgelegt werden. Dazu führt man einen Bezugspfeil längs der Leitung ein. Das Vorzeichen der Stromstärke bezüglich des Pfeils überträgt sich auf die Bilanz bezüglich des Speichers, auf den der Pfeil zeigt. Bezüglich des Speichers am andern Ende der Leitung ist die gleiche Stromstärke mit dem entgegengesetzten Vorzeichen zu bilanzieren. Beim Zihlkanal wird ein Strom, der vom Neuenburger zum Bielersee fliesst, positiv gezählt. Fliesst nun das Wasser wie am 10. August 2007 vom Bielersee in den Neuenburgersee, hat der Volumenstrom eine negative Stärke. Dieser Wert wird in der Volumenbilanz bezüglich des Bielersees direkt und in die Bilanz bezüglich des Neuenburgersees mit umgekehrtem Vorzeichen verrechnet. Die systemdynamischen Modellierungstools wenden die Vorzeichenregel genau so an. Zeigt eine Flussgrösse (Pipeline) in die Bestandesgrösse (Topf) hinein, wird eine gegebene Stromstärke direkt in die Bilanz eingefügt. Zeigt die Flussgrösse hinaus, wird in der Bilanz die zugehörige Stromstärke subtrahiert.
Nun wollen wir die Bilanz bezüglich des Bielersees zum Zeitpunkt 8. August 2007 24 Uhr auswerten. Zu diesem Zeitpunt strömten durch den Hagneckkanal 1170 m3/s in den Bielersee hinein, die Schüss brachte zusätzlich 45 m3/s und aus dem Ziehlkanal flossen 140 m3/s gegen den Neuenburgersee. Der Pegel des Bilersees stieg mit einer Geschwindigkeit von 1.9 10-5 m/s, was auf den ganzen See hochgerechnet eine Änderungsrate von 760 m3/s ergibt. Folglich mussten 315 m3/s über den Nidau-Büren-Kanal abgeflossen sein. Die Messstelle in Brügg hat einen Wert von 280 m3/s festgestellt. Wie können wir die Differenz erklären?
Drei Gründe für diesen Unterschied zwischen theoretischer Vorhersagen (Bilanzgleichung) und der Messung können geltend gemacht werden:
- weitere Zuflüsse und Quellenterme (Dauerregen)
- Grösse des Sees (kein homogenes System, Wind kann den Seespiegel verformen)
- Laufzeit der Flutwelle
Wie stark diese Störterme die Bilanz beeinflussen, ist schwer abzuschätzen. Die folgenden Bemerkungen sollen Hinweise für eine erste Beurteilung liefern
- In den Bielersee fliessen einige Bäche. Dazu kommt noch das Oberflächenwasser der Umgebung. Insgesamt dürfte dies alles zusammen kaum mehr als die Suze ausmachen. Ein kräftiger Regen kann 10 bis 50 mm Niederschlag pro Stunde bringen. Geht man von 20 mm aus, gibt das auf den Bielersee hochgerechnet etwa 220 m3/s. Die Wirkung der Bäche und des Oberflächenwassers auf die Bilanz könnte mit einer grösseren Fläche bei der Berechnung der Regenmenge berücksichtigt werden.
- Der Pegel wird bei Ligerz gemessen. Weil die Seeoberfläche durch den Wind bewegt werden kann, müsste man an mehreren Stellen des Sees den Pegelstand ermitteln.
- Ergiesst sich plötzlich ein starker Strom in den See, dauert es eine gewisse Zeit, bis sich dieses Wasser auf den ganzen See verteilt hat. Zudem müsste man noch wissen, wie weit die Messstelle Brügg vom Ausfluss aus dem Bielersee entfernt ist. Je weiter flussabwärts eine Messstelle gelegen ist, umso länger dauert es, bis sich dort eine Änderung der Stromstärke bemerkbar macht.
Modellbildung
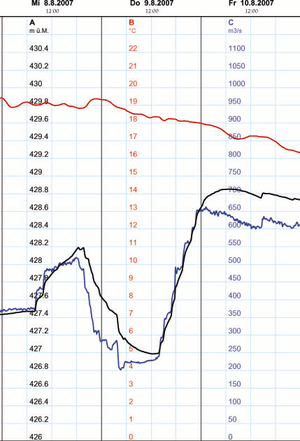
Durch den Nidau-Büren-Kanal sind in der kritischen Phase maximal 500 m3/s geflossen. Dieser Strom hätte die "Murgenthaler-Bedingung" nicht verletzen können. Andere Flüsse haben das ihre beigetragen. So hat in der fraglichen Nacht allein die Emme 600 m3/s in die Aare eingebracht. Die Idee wäre aber gewesen, dass man den Ausfluss aus dem Bielersee so weit drosselt, dass trotz der Emme und ein paar weiterer Flüssen die "Murgenthaler-Bedingung" erfüllt geblieben wäre. Weil alle diese Wassermengen eine gewisse Zeit brauchen, bis sie den Kanton Aargau erreichen, muss man das ganze hydraulische System der Aare und ihrer Zuflüsse in ein Simulationsmodell abbilden.
Modelle ganzer Flusssysteme sind - wie das Beispiel zeigt - nicht einfach zu erstellen. Das ist Aufgabe der Spezialisten. Sie werden in diesem Kurs aber lernen, wie man Modelle einfacher Systeme (homogen, wenige Zustandsgrössen) baut, wie man die Simulationsergebnisse mit Messungen vergleicht und wie man ein Modell an die Messdaten anpasst.
Kontrollfragen
- Formulieren Sie die Volumenbilanz bezüglich des Bielersees.
- Am 30. August 2007 hat der Rhein 2400 m3 Wasser pro Sekunde durch Basel transportiert. Wie schnell wäre das Wasser im Mittel geflossen, wenn der Rheins dort einen rechteckigen Querschnitt von 200 m auf 3 m hätte?
- Welchen Wert hat die Volumenänderungsrate des Bielersees am 9. August 2007 im Mittel angenommen?
- Wie viel Wasser ist am 9. August 2007 durch den Hagneck-Kanal in den Bieldersee geflossen?
- Um wie viel wäre der Bielersee an diesem Tag gestiegen, wenn keine weiteren Zu- und Abflüsse vorhanden gewesen wären?
Antworten zu den Kontrollfragen
- Die Summe über die Volumenstromstärken von Schüss, Twannbach, Hagneck-, Zihl- und Nidau-Büren-Kanal ist gleich der Volumenänderungsrate des Bielersees. In dieser Bilanz sind die Beiträge der kleinen Bäche, des Oberflächenwassers, des Regens und der Verdunstung nicht aufgeführt. Die Vernichtung und Erzeugung von Wasser durch chemische und biologische Aktivitäten fallen kaum ins Gewicht.
- Die mittlere Strömungsgeschwindigkeit ist definiert als Quotient aus Volumenstrom und Querschnitt: [math]\overline v=\frac{I_V}{A}[/math] = 4 m/s.
- Am 9. August 2007 ist der Spiegel des Bielersees von 429.85 m auf 430.9 m gestiegen. Multipliziert man diesen Höhenunterschied von 1.05 m mit der Fläche des Sees (39.3 km2), erhält man die gesamte Volumenänderung. Eine Division durch 86400 s liefert danach den gesuchten Wert von etwa 480 m3/s.
- Am 9. August 2007 strömten im Mittel etwa 1200 m3/s durch den Hagneck-Kanal. Multipliziert man diesen Wert mit 86400 s, erhält 1.04*108 m3 oder 0.104 km3 Wasser.
- Wäre nur Wasser durch den Hagneck-Kanal zugeflossen, hätte sich der Spiegel des Bieldersees um etwa [math]\Delta h=\frac{\Delta V}{A}[/math] = 2.6 m gehoben.
Materialien
- Skript Seite 1
- Physik - Ein systemdynamischer Zugang für die Sekundarstufe II Seiten 23 - 33
- eLearning Teilmodule Einführung und Volumenbilanz
- Videoaufzeichnung
- Kurzfassung auf Yotube