Trägheit als Induktivität: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) |
||
| (51 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[resistives Gesetz|Widerstand]] und [[kapazitives Gesetz|Kapazität]] |
Thema dieser Vorlesung ist die '''hydraulische Induktivität'''. Die schon bekannten Elemente, [[resistives Gesetz|Widerstand]] und [[kapazitives Gesetz|Kapazität]], beschreiben die primären Eigenschaften von Leitungen und Gefässen. Modelliert man ein System nur mit diesen beiden Elementen, können Ausgleichsvorgänge, aber keine Schwingungen simuliert werden. Schwingungsfähige Systeme weisen neben Kapazitäten und Widerständen auch noch [[induktives Gesetz|Induktivitäten]] auf. |
||
== Lernziele == |
|||
In dieser Vorlesung lernen Sie |
|||
*wie ein induktives Element das Systemverhalten beeinflusst |
|||
*von welchen Einflussgrössen die hydraulische Induktivität eines [[langes Rohr|langen Rohrstückes]] abhängt |
|||
*wie die induktiv gespeicherte [[Energie]] zu berechnen ist |
|||
*wie sich ein Speicher mit konstanter Kapazität bei laminarem Abfluss verhält |
|||
*wie man die Schwingungsdauer in einem U-Rohr rechnet |
|||
==kommunizierende Gefässe== |
==kommunizierende Gefässe== |
||
[[Bild:URohr.jpg|thumb|U-Rohr]] |
[[Bild:URohr.jpg|thumb|U-Rohr]] |
||
Sind zwei Behälter über eine Leitung miteinander verbunden, nennt man die ganze Anordnung [[kommunizierende Gefässe]]. |
Sind zwei Behälter über eine Leitung miteinander verbunden, nennt man die ganze Anordnung [[kommunizierende Gefässe]]. Füllt man eines der beiden Gefässe und lässt das andere zuerst leer, fliesst ein Ausgleichstrom, bis das Niveau in beiden Gefässen gleich hoch ist. Wie dieser Vorgang zu modellieren ist, sollten Sie in der Zwischenzeit gelernt haben. Nun denken wir uns die Verbindungsleitung immer dicker, bis die zwei Gefässe und das dazwischen liegende Verbindungsstück zu einem ''U''-förmigen Rohr verschmolzen sind. Wird nun die Flüssigkeit auf der einen Seite des U-Rohres angehoben und dann los gelassen, beginnnt die Flässigkeitssäule zu schwingen. |
||
Wie bringt man das mit Flüssigkeit gefüllte Rohr im [[System Dynamics|systemdynamischen Modell]] zum Schwingen? Der Versuch, den Widerstand zu verkleinern |
Wie bringt man nun das mit Flüssigkeit gefüllte Rohr im [[System Dynamics|systemdynamischen Modell]] zum Schwingen? Der Versuch, den Widerstand zu verkleinern, bringt nichts. Mit dieser Massnahme verkürzt man nur die Zeit, bis sich die Niveaus angeglichen haben. Es braucht eine weitere, neuartige Systemeigenschaft, um eine Schwingung zu erzwingen. Vergleichen wir nochmals die Bewegung im U-Rohr mit dem Ausgleichsvorgang in zwei kommunizierenden Gefässen: |
||
*Bewegungsverhalten der Flüssigkeit: |
|||
**im U-Rohr bewegt sich die Flüssigkeit beschleunigt auf den Gleichgewichtszustand zu |
|||
**bei den kommunizierenden Gefässen klingt der Volumenstrom bis zum Ausgleich stetig ab |
|||
*Energiebetrachtung |
|||
**im U-Rohr wird Gravitationsenergie in Bewegungsenergie "umgewandelt" |
|||
**bei den kommunizierenden Gefässen wird Gravitationsenergie im Rohr [[Dissipation|dissipiert]]. |
|||
'''Abgrenzung gegen die Translationsmechanik''': In der [[Hydrodynamik]] äussert sich die Trägheit der Flüssigkeit (Speicher für die [[Bewegungsenergie]]) durch ein [[induktives Gesetz|induktives Verhalten]]. Später werden Sie lernen, dass die Trägheit in der [[Translationsmechanik]] als Kapazität in Erscheinung tritt. Die Tatsache, dass die Trägheit oder die träge [[Masse]] einmal induktiv ([[Hydrodynamik]]) und einmal kapazitiv ([[Translationsmechanik]]) wirkt, nennt man '''Dualität'''. |
|||
==Definition== |
==Definition== |
||
Der Begriff Induktivität entstammt der [[Elektrodynamik]] und wird dort vom Induktionsgesetz her erklärt. In der |
[[Bild:Rohrbruch.jpg|thumb|Rohrbruch infolge Druckstoss]] Der Begriff Induktivität entstammt der [[Elektrodynamik]] und wird dort vom [[Induktionsgesetz]] her erklärt. In der hier zu entwickelnden [[Physik der dynamischen Systeme]] löst man sich von den historischen Wurzeln und homologisiert die Elemente über alle Bereiche. Diese generalisierte Sicht beschreibt die Induktivität als Beharrungsvermögen eines beliebigen Stromes ([[Volumen]], [[elektrische Ladung]], [[Impuls]], [[Drehimpuls]]). Diese Eigenschaft des Beharrens ist in der [[Hydrodynamik]] offensichtlich: |
||
*schliesst man ein Ventil, wirkt die Trägheit der Flüssigkeit dem Abklingen des Stromes entgegen |
|||
*die gleiche Trägheit widersetzt sich dem Anwachsen des Volumenstromes nach dem Öffnen des Ventils. |
|||
==> '''Induktivität beschreibt die Trägheit eines Stromes'''. |
|||
Schliesst man den Kugelhahn bei deiner Wasserleitung sehr schnell, kann man den Schlag der abzubremsenden Wassersäule gegen das geschlossene Ventil direkt hören. Würde man das Wasser durch das mehr als zehn Mal dichtere Quecksilber ersetzen, würde dieses im schlimmsten Fall das Ventil zerstören oder die Leitung zum Platzen bringen. Jede Flüssigkeitssäule, die abgebremst wird, erzeugt an der Stirnseite einen Überdruck. Diese Eigenschaft führt uns direkt zur Definition der Induktivität: die hydraulische Induktivität ''L<sub>V</sub>'' beschreibt das Verhältnis von '''Druckdifferenz''' über dem Element zur '''Änderungsrate der Volumenstromstärke''' |
|||
Schliesst man den Kugelhahn in einer Wasserleitung sehr schnell, ist der Schlag des Wassers gegen den Verschluss des Hahns direkt zu hören. Wird das Wasser durch das mehr als zehn Mal dichtere Quecksilber ersetzt, kann im schlimmsten Fall der Verschluss zerstört oder die Leitung zum Platzen gebracht werden. Jede Flüssigkeitssäule, die abgebremst wird, erzeugt an ihrer Stirnseite einen Überdruck. Diese Eigenschaft führt uns direkt zur Definition der Induktivität: die hydraulische Induktivität ''L<sub>V</sub>'' beschreibt das Verhältnis von '''Druckdifferenz''' über dem Rohr zur '''Änderungsrate der Volumenstromstärke''' |
|||
:<math>\Delta p=L_V\dot I_V</math> |
:<math>\Delta p=L_V\dot I_V</math> |
||
Gemäss dieser Definition wird die Induktivität in Pas<sup>2</sup> / m<sup>3</sup> gemessen. |
Gemäss dieser Definition wird die Induktivität in Pas<sup>2</sup> / m<sup>3</sup> gemessen. |
||
Das induktive Verhalten eines Leitungsstückes macht sich solange nicht bemerkbar, wie die Stromstärke konstant bleibt. Bei einem stationär fliessenden Strom sorgt nur der (laminare oder turbulente) Widerstand für eine Druckgefälle. Erst wenn der Volumenstrom stärker werden soll, muss die zusätzliche Druckdifferenz angelegt werden. Induktives und resistives Druckgefälle wirken dann auf die gleiche Seite. Soll der Volumenstrom schwächer werden, muss eine zusätzliche Druckdifferenz gegen die Strömung wirken. Induktives und resistives Druckgefälle wirken dann gegeneinander. |
|||
[[Bild:Delta p IV.gif|thumb|Druckdifferenz und Volumenstrom]] Das Trägheits-Verhalten des Stromes kann auch von der Bewegungsenergie her erklärt werden: ein anschwellender Strom ist ein Verbraucher, da er Energie aufnehmen muss, und ein abschwellender Strom verhält sich wie ein Antrieb, weil er Energie abgibt. |
|||
Zusammenfassend kann die Wirkung der Induktivität eines Leitungsabschnittes wir folgt beschrieben werden |
|||
*ein '''anschwellender''' Volumenstrom benötigt eine '''antreibende''' Druckdifferenz |
|||
*eine '''gegen''' den Strom gerichtete Druckdifferenz '''verringert''' den Betrag des Volumenstromstärke |
|||
Gemäss Definition ist die induktiv erzeugte Druckdifferenz gleich Induktivität mal Änderungsrate der Volumenstromstärke. Wird nun der Wasserstrom in einer Leitung schnell unterbrochen, hängt die Höhe der Druckspitze von der Grösse der Induktivität und der Abbremszeit ab. Je schneller ein Ventil geschlossen wird und je grösser die Induktivität ist, desto grösser wird die Druckspitze an der Stirnseite der Flüssigkeitssäule. |
|||
== langes Rohr == |
== langes Rohr == |
||
Die hydraulische Induktivität eines beliebig geformten Rohrleitungsabschnittes ist nicht elementar berechenbar. Für ein gerades, [[langes Rohr]] kann dagegen eine einfache Formel angegeben werden |
|||
:<math>L_V=\varrho \frac {l}{A}</math> |
|||
Dass die Induktivität proportional zur Dichte der Flüssigkeit und zur Länge des Rohres ist, leuchtet unmittelbar ein. Dass noch durch den Querschnitt dividiert werden muss, hängt mit der Geometrie zusammen. Setzt man die Berechnungsformel für die Induktivität eines langen Rohres in die Definitionsgleichung der Induktivität ein, erhält man |
|||
:<math>\Delta p=\varrho \frac {l}{A}\dot I_V=\varrho l \dot v</math> |
|||
Die induzierte Druckdifferenz ist somit gleich Dichte mal Länge mal Änderungsrate der Geschwindigkeit (Beschleunigung). Und dieser Zusammenhang entspricht etwa dem, was man mit Nachdenken erraten könnte. Im Nenner der Berechnungsformel für die Induktivität erscheint der Rohrquerschnitt, weil die Stärke des Volumenstromes proportional mit der Querschnittfläche zunimmt. |
|||
== Energie == |
== Energie == |
||
Induktive und kapazitive Elemente speichern Energie. Bei einer hydraulischen Kapazität wird die Energie zusammen mit dem Volumen aufgenommen und gespeichert, wogegen bei einer hydraulischen Induktivität die Energie an den durchfliessenden Volumenstrom gebunden ist. |
|||
[[Bild:Induktive Energie IV Delta p t.png|thumb|''I<sub>V</sub>-Δp-t-''Schaubild]]Zur quantitaiven Analyse denken wir uns einen Rohrstück, das sich rein induktiv verhält, d.h. das Element soll kein resistives Verhalten zeigen. Erzeugt man über diesem reibungsfreien Rohrabstück eine Druckdifferenz, wird der Volumenstrom immer stärker. Die Änderungsrate der Stromstärke bleibt so lange konstant, wie die Druckdifferenz aufrecht erhalten bleibt |
|||
:<math>\dot I_V=\frac{\Delta p}{L_V}</math> |
|||
oder mit der Volumenstromstärke zum Zeitnullpunkt gleich Null |
|||
:<math>I_V=\frac{\Delta p}{L_V}t</math> |
|||
Im Volumenstrom-Druck-Zeit-Schaubild ergibt dieses Verhalten wiederum einen Keil, mit einem Inhalt von |
|||
:<math>W=\frac {1}{2}I_V\Delta p t=\frac {1}{2}I_V L_V \dot I_V t = \frac {1}{2}L_V I_V^2</math> |
|||
Die induktiv gespeicherte Energie ist gleich halbe Induktivität mal Volumenstromstärke im Quadrat. |
|||
==Speicher entleeren== |
|||
In der letzten [[Widerstand und Speicher|Vorlesung]] haben Sie die [[kapazitives Gesetz|Kapazität]] und den [[resistives Gesetz|Widerstand]] als Elemente eines dynamischen Systems kennen gelernt. Versieht man nun einen Speicher, der eine konstante Kapazität aufweist, mit einem Abfluss, dessen hydraulischer Widerstand nicht von der Stromstärke abhängt (laminare Strömung), erhält man ein sogenanntes ''RC-''Glied. Um die Dynamik eines solchen Systems zu verstehen, schreiben wir die Volumenbilanz hin |
|||
:<math>\dot V=-I_V</math> |
|||
ersetzen das gespeicherte Volumen mit Hilfe des kapazitiven Gesetzes |
|||
:<math>C_V=\frac{V}{p}</math> bzw. <math>\dot V=C_V \dot p</math> |
|||
und schreiben für die Stromstärke (wir nehmen hier an, dass die Druckdifferenz über dem Abfluss gleich dem Druck im Speicher ist) |
|||
:<math>R_V=\frac{\Delta p}{I_V}=\frac{p}{I_V}</math> bzw. <math>I_V=\frac{p}{R_V}</math> |
|||
Damit erhalten wir eine Beziehung, welche besagt, dass die Änderungsrate des Drucks direkt proportional zum Druck ist |
|||
:<math>C_V \dot p=-\frac{p}{R_V}</math> oder <math>R_VC_V\dot p+p=0</math> |
|||
Aus der Gleichung geht hervor, dass das Produkt aus Kapazität und Widerstand die Einheit der Zeit haben muss. Deshalb definieren wir dieses Produkt als Zeitkonstante ''τ'' |
|||
:<math>\tau\dot p+p=0</math> mit <math>\tau=R_VC_V</math> |
|||
Diese Differentialgleichung erster Ordnung mit konstanten Koeffizienten hat eine einfache Lösung |
|||
:<math>p=p_0e^{-t/\tau}</math> |
|||
oder mit Hilfe Widerstandsgesetzes auf die Stromstärke umgerechnet |
|||
:<math>I_V=I_{V0}e^{-t/\tau}</math> mit <math>I_{V0}=\frac{p_0}{R_V}</math> |
|||
== U-Rohr == |
== U-Rohr == |
||
[[Bild:Wasserpendel.png|thumb|U-Rohr-Schwinger]] Systemdynamisch gesehen besteht ein mit einer Flüssigkeit gefülltes U-Rohr aus zwei Kapazitäten (beide Schenkel), einem Widerstand (mit Flüssigkeit gefüllter Teil des Rohres) und einer Induktivität (mit Flüssigkeit gefüllter Teil des Rohres). Alle vier Elemente können als in Serie geschaltet angesehen werden. Lässt man den Widerstand weg, erhält man einen ungedämpften Schwingkreis, bestehend aus der Indukitivität des Rohres und der halben Kapazität eines der beiden vertikal stehenden Schenkels (zylinderförmiges Gefäss). Die halbe Kapazität ergibt sich aus dem Umstand, dass bei Serieschaltung die Kapazitäten reziprok genommen zur reziproken Gesamtkapazität addiert werden müssen. |
|||
Für die Periode (hin und zurück) eines Schwingkreises findet man in jedem Lehrbuch zur Elektrotechnik die folgende Formel |
|||
:<math>T=2\pi\sqrt{LC}</math> |
|||
Nun ist die Kapazität eines zylinderförmigen Gefässes gleich |
|||
:<math>C_V=\frac{A}{\varrho g}</math> |
|||
und für die Induktivität eines [[langes Rohr|langen Rohres]] gilt |
|||
:<math>L_V=\varrho\frac{l}{A}</math> |
|||
Setzt man die Induktivität und die halbe Kapazität in die Formel für den elektrischen Schwingkreis ein, erhält man |
|||
:<math>T=2\pi \sqrt{\frac{l}{2g}}</math> |
|||
Die Schwingungsdauer der Flüssigkeitsspiegel sind unabhängig von der Dichte und vom Querschnitt. Folglich schwingt Quecksilber gleich schnell wie Wasser, wenn die beiden mit Flüssigkeit gefüllten Leitungsabschnitte gleich lang sind. |
|||
Dieses Beispiel zeigt exemplarisch, wie in der [[Physik der dynamischen Systeme]] die verschiedenen Gebiete miteinander vernetzt werden und wie so der Lernprozess optimiert werden kann. |
|||
==weitere Anwendungen== |
|||
[[Bild:Hydraulischer_Widder.jpg|thumb|hydraulischer Widder]] Die hydraulische [[induktives Gesetz|Induktivität]] eines [[langes Rohr|langen Rohres]] ist gleich Dichte mal Länge durch Querschnitt. Diese drei Einflussgrössen bestimmen die Induktivität einer Rohrleitung. |
|||
*Die hydraulische Induktivität nimmt wie der Widerstand proportional zur Länge des Rohres zu. Folglich ist das Verhältnis von Widerstand zu Induktivität unabhängig von der Länge des Rohres. |
|||
*Je dichter eine Flüssigkeit ist, desto stärker macht sich die hydraulische Induktivität bemerkbar. Nur haben die meisten Flüssigkeiten ähnliche Dichten. Eine wichtige Ausnahme bildet das Quecksilber. |
|||
*Die Induktivität nimmt mit dem Durchmesser des Rohres im Quadrat ab, der turbulente Widerstand geht dagegen mit dem Durchmesser hoch fünf zurück. Folglich macht sich die hydraulische Induktivität bei grossen Leitungen stärker bemerkbar. |
|||
In Hochdruck-Wasserkraftwerken ist die hydraulische Induktivität eine unerwünschte Erscheinung. Wird ein Druckschieber schnell geschlossen, erzeugt die hydraulische Induktivität eine derart grosse Druckspitze, dass die Stollen und Rohre bersten können. Um die vom Schieber rückwärts nach oben laufende Druckwelle aufzufangen, besitzt jedes Hochdruck-Wasserkraftwerk ein Wasserschloss. |
|||
Im [[hydraulischer Widder|hydraulischen Widder]] nutzt man die induktive Wirkung des fliessenden Wassers aus, um einen kleinen Teil davon hinauf zu pumpen. |
|||
== Kontrollfragen == |
|||
#Die [[Physik der dynamischen Systeme]] kennt drei lineare Elemente: [[resistives Gesetz|Widerstand]], [[kapazitives Gesetz|Kapazität]] und [[induktives Gesetz|Induktivität]]. Formulieren Sie mit Ihren eigenen Worten, wie |
|||
##der (laminare) Strömungswiderstand definiert ist? |
|||
##wie die hydraulische Kapazität definiert ist? |
|||
##wie die hydraulische Induktivität definiert ist? |
|||
#Welche Einflussgrössen bestimmen die hydraulische Induktivität eines langen Rohres? |
|||
#Wie berechnet sich die induktiv gespeicherte Energie? |
|||
#Wie lange dauert es, bis ein Gefäss mit konstanter Kapazität durch einen laminaren Strom bis auf 1% entleert ist (in Zeitkonstanten ausgedrückt)? |
|||
#Wie ändert sich die Schwingungsdauer in einem U-Rohr, wenn man |
|||
##Wasser durch Quecksilber ersetzt? |
|||
##das Rohr länger macht? |
|||
##ein dickeres Rohr nimmt? |
|||
##die Flüssigkeit im U-Rohr auf dem Mond schwingen lässt? |
|||
==Antworten zu den Kontrollfragen== |
|||
#Die Definitionen für die drei linearen Systemeigenschaften lauten |
|||
##Strömungswiderstand: <math>R_V=\frac{\Delta p}{I_V}</math> , der Widerstand bestimmt das Verhältnis von angelegter Druckdifferenz zur Stärke des fliessenden Stroms |
|||
##Kapazität: <math>C_V=\frac{\Delta V}{\Delta p}</math> , die Kapazität legt fest, wie viel Volumen ein Speicher pro Druckanstieg aufnehmen kann |
|||
##Induktivität: <math>L_V=\frac{\Delta p}{\dot I_V}</math> , die Induktivität besagt, wie die angelegte Druckdifferenz das Wachstum der Stromstärke beeinflusst |
|||
#Die hydraulische Induktivität eines langen Rohrs ist proportional zur Dichte der Flüssigkeit und zur Länge des Rohres. Sie ist umgekehrt proportional zur Querschnittsfläche des Rohrs. |
|||
#Die induktiv gespeicherte Energie ist proportional zum Quadrat der Stromstärke: <math>W_{ind}=\frac {L_V}{2}I_V^2</math> |
|||
#Der Druck und damit auch das Volumen nehmen exponentiell mit der Zeit ab: <math>p=p_0e^{-t/\tau}</math>. Setzt man nun für den Enddruck einen hundertstel des Anfangsdrucks ein und löst nach der Zeit auf, folgt <math>t=\tau\ln 100=4.6\tau</math>. |
|||
#Die Schwingungsdauer (Periode) eines U-Rohrs ist unabhängig von der Dichte der Flüssigkeit und vom Rohrquerschnitt. Sie hängt nur von der Länge des Rohrs und von der Gravitationsfeldstärke ab. Folglich würden die Flüssigkeitsspiegel auf dem Mond langsamer schwingen. |
|||
== Materialien == |
|||
*[https://home.zhaw.ch/~mau/Lehre/Skript/HydraulikT.pdf Skript] Seite 5 |
|||
*[http://www.pegaswiss.ch/Hydrodynamik/index.php eLearning] Teilmodul Induktivität |
|||
*[https://cast.switch.ch/vod/clips/xmqyafm3m/link_box Videoaufzeichnung] |
|||
*[http://www.youtube.com/watch?v=dE0UDCwMVEM Kurzfassung auf Yotube] |
|||
'''[[Physik und Systemwissenschaft in Aviatik 2014]]''' |
|||
'''[[Physik und Systemwissenschaft in Aviatik]]''' |
|||
[[Kategorie:VorAV]] |
|||
Aktuelle Version vom 5. Oktober 2015, 08:04 Uhr
Thema dieser Vorlesung ist die hydraulische Induktivität. Die schon bekannten Elemente, Widerstand und Kapazität, beschreiben die primären Eigenschaften von Leitungen und Gefässen. Modelliert man ein System nur mit diesen beiden Elementen, können Ausgleichsvorgänge, aber keine Schwingungen simuliert werden. Schwingungsfähige Systeme weisen neben Kapazitäten und Widerständen auch noch Induktivitäten auf.
Lernziele
In dieser Vorlesung lernen Sie
- wie ein induktives Element das Systemverhalten beeinflusst
- von welchen Einflussgrössen die hydraulische Induktivität eines langen Rohrstückes abhängt
- wie die induktiv gespeicherte Energie zu berechnen ist
- wie sich ein Speicher mit konstanter Kapazität bei laminarem Abfluss verhält
- wie man die Schwingungsdauer in einem U-Rohr rechnet
kommunizierende Gefässe
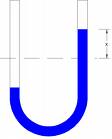
Sind zwei Behälter über eine Leitung miteinander verbunden, nennt man die ganze Anordnung kommunizierende Gefässe. Füllt man eines der beiden Gefässe und lässt das andere zuerst leer, fliesst ein Ausgleichstrom, bis das Niveau in beiden Gefässen gleich hoch ist. Wie dieser Vorgang zu modellieren ist, sollten Sie in der Zwischenzeit gelernt haben. Nun denken wir uns die Verbindungsleitung immer dicker, bis die zwei Gefässe und das dazwischen liegende Verbindungsstück zu einem U-förmigen Rohr verschmolzen sind. Wird nun die Flüssigkeit auf der einen Seite des U-Rohres angehoben und dann los gelassen, beginnnt die Flässigkeitssäule zu schwingen.
Wie bringt man nun das mit Flüssigkeit gefüllte Rohr im systemdynamischen Modell zum Schwingen? Der Versuch, den Widerstand zu verkleinern, bringt nichts. Mit dieser Massnahme verkürzt man nur die Zeit, bis sich die Niveaus angeglichen haben. Es braucht eine weitere, neuartige Systemeigenschaft, um eine Schwingung zu erzwingen. Vergleichen wir nochmals die Bewegung im U-Rohr mit dem Ausgleichsvorgang in zwei kommunizierenden Gefässen:
- Bewegungsverhalten der Flüssigkeit:
- im U-Rohr bewegt sich die Flüssigkeit beschleunigt auf den Gleichgewichtszustand zu
- bei den kommunizierenden Gefässen klingt der Volumenstrom bis zum Ausgleich stetig ab
- Energiebetrachtung
- im U-Rohr wird Gravitationsenergie in Bewegungsenergie "umgewandelt"
- bei den kommunizierenden Gefässen wird Gravitationsenergie im Rohr dissipiert.
Abgrenzung gegen die Translationsmechanik: In der Hydrodynamik äussert sich die Trägheit der Flüssigkeit (Speicher für die Bewegungsenergie) durch ein induktives Verhalten. Später werden Sie lernen, dass die Trägheit in der Translationsmechanik als Kapazität in Erscheinung tritt. Die Tatsache, dass die Trägheit oder die träge Masse einmal induktiv (Hydrodynamik) und einmal kapazitiv (Translationsmechanik) wirkt, nennt man Dualität.
Definition

Der Begriff Induktivität entstammt der Elektrodynamik und wird dort vom Induktionsgesetz her erklärt. In der hier zu entwickelnden Physik der dynamischen Systeme löst man sich von den historischen Wurzeln und homologisiert die Elemente über alle Bereiche. Diese generalisierte Sicht beschreibt die Induktivität als Beharrungsvermögen eines beliebigen Stromes (Volumen, elektrische Ladung, Impuls, Drehimpuls). Diese Eigenschaft des Beharrens ist in der Hydrodynamik offensichtlich:
- schliesst man ein Ventil, wirkt die Trägheit der Flüssigkeit dem Abklingen des Stromes entgegen
- die gleiche Trägheit widersetzt sich dem Anwachsen des Volumenstromes nach dem Öffnen des Ventils.
==> Induktivität beschreibt die Trägheit eines Stromes.
Schliesst man den Kugelhahn in einer Wasserleitung sehr schnell, ist der Schlag des Wassers gegen den Verschluss des Hahns direkt zu hören. Wird das Wasser durch das mehr als zehn Mal dichtere Quecksilber ersetzt, kann im schlimmsten Fall der Verschluss zerstört oder die Leitung zum Platzen gebracht werden. Jede Flüssigkeitssäule, die abgebremst wird, erzeugt an ihrer Stirnseite einen Überdruck. Diese Eigenschaft führt uns direkt zur Definition der Induktivität: die hydraulische Induktivität LV beschreibt das Verhältnis von Druckdifferenz über dem Rohr zur Änderungsrate der Volumenstromstärke
- [math]\Delta p=L_V\dot I_V[/math]
Gemäss dieser Definition wird die Induktivität in Pas2 / m3 gemessen.
Das induktive Verhalten eines Leitungsstückes macht sich solange nicht bemerkbar, wie die Stromstärke konstant bleibt. Bei einem stationär fliessenden Strom sorgt nur der (laminare oder turbulente) Widerstand für eine Druckgefälle. Erst wenn der Volumenstrom stärker werden soll, muss die zusätzliche Druckdifferenz angelegt werden. Induktives und resistives Druckgefälle wirken dann auf die gleiche Seite. Soll der Volumenstrom schwächer werden, muss eine zusätzliche Druckdifferenz gegen die Strömung wirken. Induktives und resistives Druckgefälle wirken dann gegeneinander.

Das Trägheits-Verhalten des Stromes kann auch von der Bewegungsenergie her erklärt werden: ein anschwellender Strom ist ein Verbraucher, da er Energie aufnehmen muss, und ein abschwellender Strom verhält sich wie ein Antrieb, weil er Energie abgibt.
Zusammenfassend kann die Wirkung der Induktivität eines Leitungsabschnittes wir folgt beschrieben werden
- ein anschwellender Volumenstrom benötigt eine antreibende Druckdifferenz
- eine gegen den Strom gerichtete Druckdifferenz verringert den Betrag des Volumenstromstärke
Gemäss Definition ist die induktiv erzeugte Druckdifferenz gleich Induktivität mal Änderungsrate der Volumenstromstärke. Wird nun der Wasserstrom in einer Leitung schnell unterbrochen, hängt die Höhe der Druckspitze von der Grösse der Induktivität und der Abbremszeit ab. Je schneller ein Ventil geschlossen wird und je grösser die Induktivität ist, desto grösser wird die Druckspitze an der Stirnseite der Flüssigkeitssäule.
langes Rohr
Die hydraulische Induktivität eines beliebig geformten Rohrleitungsabschnittes ist nicht elementar berechenbar. Für ein gerades, langes Rohr kann dagegen eine einfache Formel angegeben werden
- [math]L_V=\varrho \frac {l}{A}[/math]
Dass die Induktivität proportional zur Dichte der Flüssigkeit und zur Länge des Rohres ist, leuchtet unmittelbar ein. Dass noch durch den Querschnitt dividiert werden muss, hängt mit der Geometrie zusammen. Setzt man die Berechnungsformel für die Induktivität eines langen Rohres in die Definitionsgleichung der Induktivität ein, erhält man
- [math]\Delta p=\varrho \frac {l}{A}\dot I_V=\varrho l \dot v[/math]
Die induzierte Druckdifferenz ist somit gleich Dichte mal Länge mal Änderungsrate der Geschwindigkeit (Beschleunigung). Und dieser Zusammenhang entspricht etwa dem, was man mit Nachdenken erraten könnte. Im Nenner der Berechnungsformel für die Induktivität erscheint der Rohrquerschnitt, weil die Stärke des Volumenstromes proportional mit der Querschnittfläche zunimmt.
Energie
Induktive und kapazitive Elemente speichern Energie. Bei einer hydraulischen Kapazität wird die Energie zusammen mit dem Volumen aufgenommen und gespeichert, wogegen bei einer hydraulischen Induktivität die Energie an den durchfliessenden Volumenstrom gebunden ist.
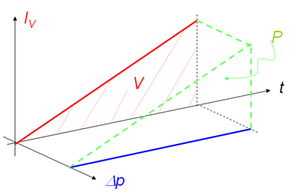
Zur quantitaiven Analyse denken wir uns einen Rohrstück, das sich rein induktiv verhält, d.h. das Element soll kein resistives Verhalten zeigen. Erzeugt man über diesem reibungsfreien Rohrabstück eine Druckdifferenz, wird der Volumenstrom immer stärker. Die Änderungsrate der Stromstärke bleibt so lange konstant, wie die Druckdifferenz aufrecht erhalten bleibt
- [math]\dot I_V=\frac{\Delta p}{L_V}[/math]
oder mit der Volumenstromstärke zum Zeitnullpunkt gleich Null
- [math]I_V=\frac{\Delta p}{L_V}t[/math]
Im Volumenstrom-Druck-Zeit-Schaubild ergibt dieses Verhalten wiederum einen Keil, mit einem Inhalt von
- [math]W=\frac {1}{2}I_V\Delta p t=\frac {1}{2}I_V L_V \dot I_V t = \frac {1}{2}L_V I_V^2[/math]
Die induktiv gespeicherte Energie ist gleich halbe Induktivität mal Volumenstromstärke im Quadrat.
Speicher entleeren
In der letzten Vorlesung haben Sie die Kapazität und den Widerstand als Elemente eines dynamischen Systems kennen gelernt. Versieht man nun einen Speicher, der eine konstante Kapazität aufweist, mit einem Abfluss, dessen hydraulischer Widerstand nicht von der Stromstärke abhängt (laminare Strömung), erhält man ein sogenanntes RC-Glied. Um die Dynamik eines solchen Systems zu verstehen, schreiben wir die Volumenbilanz hin
- [math]\dot V=-I_V[/math]
ersetzen das gespeicherte Volumen mit Hilfe des kapazitiven Gesetzes
- [math]C_V=\frac{V}{p}[/math] bzw. [math]\dot V=C_V \dot p[/math]
und schreiben für die Stromstärke (wir nehmen hier an, dass die Druckdifferenz über dem Abfluss gleich dem Druck im Speicher ist)
- [math]R_V=\frac{\Delta p}{I_V}=\frac{p}{I_V}[/math] bzw. [math]I_V=\frac{p}{R_V}[/math]
Damit erhalten wir eine Beziehung, welche besagt, dass die Änderungsrate des Drucks direkt proportional zum Druck ist
- [math]C_V \dot p=-\frac{p}{R_V}[/math] oder [math]R_VC_V\dot p+p=0[/math]
Aus der Gleichung geht hervor, dass das Produkt aus Kapazität und Widerstand die Einheit der Zeit haben muss. Deshalb definieren wir dieses Produkt als Zeitkonstante τ
- [math]\tau\dot p+p=0[/math] mit [math]\tau=R_VC_V[/math]
Diese Differentialgleichung erster Ordnung mit konstanten Koeffizienten hat eine einfache Lösung
- [math]p=p_0e^{-t/\tau}[/math]
oder mit Hilfe Widerstandsgesetzes auf die Stromstärke umgerechnet
- [math]I_V=I_{V0}e^{-t/\tau}[/math] mit [math]I_{V0}=\frac{p_0}{R_V}[/math]
U-Rohr
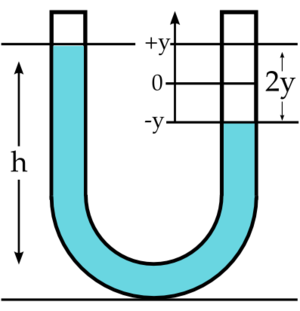
Systemdynamisch gesehen besteht ein mit einer Flüssigkeit gefülltes U-Rohr aus zwei Kapazitäten (beide Schenkel), einem Widerstand (mit Flüssigkeit gefüllter Teil des Rohres) und einer Induktivität (mit Flüssigkeit gefüllter Teil des Rohres). Alle vier Elemente können als in Serie geschaltet angesehen werden. Lässt man den Widerstand weg, erhält man einen ungedämpften Schwingkreis, bestehend aus der Indukitivität des Rohres und der halben Kapazität eines der beiden vertikal stehenden Schenkels (zylinderförmiges Gefäss). Die halbe Kapazität ergibt sich aus dem Umstand, dass bei Serieschaltung die Kapazitäten reziprok genommen zur reziproken Gesamtkapazität addiert werden müssen.
Für die Periode (hin und zurück) eines Schwingkreises findet man in jedem Lehrbuch zur Elektrotechnik die folgende Formel
- [math]T=2\pi\sqrt{LC}[/math]
Nun ist die Kapazität eines zylinderförmigen Gefässes gleich
- [math]C_V=\frac{A}{\varrho g}[/math]
und für die Induktivität eines langen Rohres gilt
- [math]L_V=\varrho\frac{l}{A}[/math]
Setzt man die Induktivität und die halbe Kapazität in die Formel für den elektrischen Schwingkreis ein, erhält man
- [math]T=2\pi \sqrt{\frac{l}{2g}}[/math]
Die Schwingungsdauer der Flüssigkeitsspiegel sind unabhängig von der Dichte und vom Querschnitt. Folglich schwingt Quecksilber gleich schnell wie Wasser, wenn die beiden mit Flüssigkeit gefüllten Leitungsabschnitte gleich lang sind.
Dieses Beispiel zeigt exemplarisch, wie in der Physik der dynamischen Systeme die verschiedenen Gebiete miteinander vernetzt werden und wie so der Lernprozess optimiert werden kann.
weitere Anwendungen
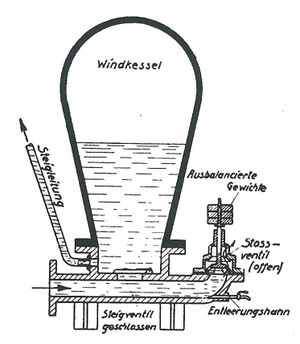
Die hydraulische Induktivität eines langen Rohres ist gleich Dichte mal Länge durch Querschnitt. Diese drei Einflussgrössen bestimmen die Induktivität einer Rohrleitung.
- Die hydraulische Induktivität nimmt wie der Widerstand proportional zur Länge des Rohres zu. Folglich ist das Verhältnis von Widerstand zu Induktivität unabhängig von der Länge des Rohres.
- Je dichter eine Flüssigkeit ist, desto stärker macht sich die hydraulische Induktivität bemerkbar. Nur haben die meisten Flüssigkeiten ähnliche Dichten. Eine wichtige Ausnahme bildet das Quecksilber.
- Die Induktivität nimmt mit dem Durchmesser des Rohres im Quadrat ab, der turbulente Widerstand geht dagegen mit dem Durchmesser hoch fünf zurück. Folglich macht sich die hydraulische Induktivität bei grossen Leitungen stärker bemerkbar.
In Hochdruck-Wasserkraftwerken ist die hydraulische Induktivität eine unerwünschte Erscheinung. Wird ein Druckschieber schnell geschlossen, erzeugt die hydraulische Induktivität eine derart grosse Druckspitze, dass die Stollen und Rohre bersten können. Um die vom Schieber rückwärts nach oben laufende Druckwelle aufzufangen, besitzt jedes Hochdruck-Wasserkraftwerk ein Wasserschloss.
Im hydraulischen Widder nutzt man die induktive Wirkung des fliessenden Wassers aus, um einen kleinen Teil davon hinauf zu pumpen.
Kontrollfragen
- Die Physik der dynamischen Systeme kennt drei lineare Elemente: Widerstand, Kapazität und Induktivität. Formulieren Sie mit Ihren eigenen Worten, wie
- der (laminare) Strömungswiderstand definiert ist?
- wie die hydraulische Kapazität definiert ist?
- wie die hydraulische Induktivität definiert ist?
- Welche Einflussgrössen bestimmen die hydraulische Induktivität eines langen Rohres?
- Wie berechnet sich die induktiv gespeicherte Energie?
- Wie lange dauert es, bis ein Gefäss mit konstanter Kapazität durch einen laminaren Strom bis auf 1% entleert ist (in Zeitkonstanten ausgedrückt)?
- Wie ändert sich die Schwingungsdauer in einem U-Rohr, wenn man
- Wasser durch Quecksilber ersetzt?
- das Rohr länger macht?
- ein dickeres Rohr nimmt?
- die Flüssigkeit im U-Rohr auf dem Mond schwingen lässt?
Antworten zu den Kontrollfragen
- Die Definitionen für die drei linearen Systemeigenschaften lauten
- Strömungswiderstand: [math]R_V=\frac{\Delta p}{I_V}[/math] , der Widerstand bestimmt das Verhältnis von angelegter Druckdifferenz zur Stärke des fliessenden Stroms
- Kapazität: [math]C_V=\frac{\Delta V}{\Delta p}[/math] , die Kapazität legt fest, wie viel Volumen ein Speicher pro Druckanstieg aufnehmen kann
- Induktivität: [math]L_V=\frac{\Delta p}{\dot I_V}[/math] , die Induktivität besagt, wie die angelegte Druckdifferenz das Wachstum der Stromstärke beeinflusst
- Die hydraulische Induktivität eines langen Rohrs ist proportional zur Dichte der Flüssigkeit und zur Länge des Rohres. Sie ist umgekehrt proportional zur Querschnittsfläche des Rohrs.
- Die induktiv gespeicherte Energie ist proportional zum Quadrat der Stromstärke: [math]W_{ind}=\frac {L_V}{2}I_V^2[/math]
- Der Druck und damit auch das Volumen nehmen exponentiell mit der Zeit ab: [math]p=p_0e^{-t/\tau}[/math]. Setzt man nun für den Enddruck einen hundertstel des Anfangsdrucks ein und löst nach der Zeit auf, folgt [math]t=\tau\ln 100=4.6\tau[/math].
- Die Schwingungsdauer (Periode) eines U-Rohrs ist unabhängig von der Dichte der Flüssigkeit und vom Rohrquerschnitt. Sie hängt nur von der Länge des Rohrs und von der Gravitationsfeldstärke ab. Folglich würden die Flüssigkeitsspiegel auf dem Mond langsamer schwingen.
Materialien
- Skript Seite 5
- eLearning Teilmodul Induktivität
- Videoaufzeichnung
- Kurzfassung auf Yotube