Einfaches Reservoir: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 15: | Zeile 15: | ||
*Ikon ''flow'' aktivieren, mit der Maus links vom Reservoir ins Systemdiagramm klicken und bis ins Reservoir hinein ziehen (Rahmen um Reservoir muss erscheinen) |
*Ikon ''flow'' aktivieren, mit der Maus links vom Reservoir ins Systemdiagramm klicken und bis ins Reservoir hinein ziehen (Rahmen um Reservoir muss erscheinen) |
||
*Flow mit '''Volumenstrom''' beschriften. |
*Flow mit '''Volumenstrom''' beschriften. |
||
|[[Bild:einfaches_Reservoir1.jpg]][[Bild:einfaches_Reservoir1a.jpg]] |
|[[Bild:einfaches_Reservoir1.jpg]]<br>[[Bild:einfaches_Reservoir1a.jpg]] |
||
|- |
|- |
||
|'''Parametrisieren:''' <br> Der Eingangsstrom soll sich gemäss folgender Beziehung verändern <br> <math>I_V=I_{V0}-I_{VPunkt}\cdot t</math> <br> Für die Stärke des Anfangsstroms ('''''I<sub>0</sub>''''') können 2 l/s und für die Änderungsrate ('''''I<sub>VPunkt</sub>''''') 0.001 l/s<sup>2</sup> angenommen werden.<br> Den Inhalt des Reservoirs setze man zum Zeitnullpunkt auf Null. |
|'''Parametrisieren:''' <br> Der Eingangsstrom soll sich gemäss folgender Beziehung verändern <br> <math>I_V=I_{V0}-I_{VPunkt}\cdot t</math> <br> Für die Stärke des Anfangsstroms ('''''I<sub>0</sub>''''') können 2 l/s und für die Änderungsrate ('''''I<sub>VPunkt</sub>''''') 0.001 l/s<sup>2</sup> angenommen werden.<br> Den Inhalt des Reservoirs setze man zum Zeitnullpunkt auf Null. |
||
| Zeile 36: | Zeile 36: | ||
|[[Bild:Einfaches_Reservoir4.jpg]] |
|[[Bild:Einfaches_Reservoir4.jpg]] |
||
|- |
|- |
||
|'''Rückkoppeln:''' <br> Das Reservoir leckt. |
|'''Rückkoppeln:''' <br> Das Reservoir leckt. Wie ''Evangelista Torricelli'' schon gezeigt hat, fliesst das Wasser gleich schnell aus einem Reservoir aus, wie ein Körper, der von der Wasseroberfläche fallen gelassen wird, am Loch vorbei fliegt. Folglich ist der Leckstrom gleich <br> <math>I_{V2}=A_L \sqrt{2gh}</math> |
||
|Der Leckstrom ist gleich einer Konstanten mal die Wurzel aus der Höhe <br> <math>k =\frac {I_{V2}}{\sqrt{h}}</math> <br> Die Konstante ''k'' lässt sich abschätzen. Nimmt man an, dass der Volumenstrom bei einer Füllhöhe von einem Meter ein Liter pro Sekunde beträgt, erhält man für die Konstante ''k'' = 0.001 {m2.5/ |
|Der Leckstrom ist gleich einer Konstanten ''k'' mal die Wurzel aus der Höhe. Die Konstante kann auch als Verhältnis der beiden Grössen geschrieben werden <br> <math>k =\frac {I_{V2}}{\sqrt{h}}</math> <br> Die Konstante ''k'' lässt sich abschätzen. Nimmt man an, dass der Volumenstrom bei einer Füllhöhe von einem Meter ein Liter pro Sekunde beträgt, erhält man für die Konstante ''k'' = 0.001 {m2.5/s} |
||
|[[Bild:Einfaches_Reservoir5.jpg|300px]] |
|[[Bild:Einfaches_Reservoir5.jpg|300px]] |
||
|- |
|- |
||
|'''Analysieren:''' <br> Das vorliegende Modell wird durch eine Differentialgleichung (nichtlinear, erster Ordnung) beschrieben. Alle |
|'''Analysieren:''' <br> Das vorliegende Modell wird durch eine Differentialgleichung (nichtlinear, erster Ordnung) beschrieben. Alle Beziehungen, die von BerkeleyMadonna erzeugt werden, sollen nun zu einer einzigen Gleichung zusammengefasst werden. Diese Differentialgleichung beschreibt das dynamische Verhalten ds Systems beschreibt. |
||
|Aktiviert man im Pull-Down-Menü '''Model''' den Befehl '''Equations''' ('''Ctrl+E'''), erscheint das abgebildete Fenster. Setzt man alle Beziehungen in die Bilanzgleichung ein, erhält man die Differentialgleichung <br> <math>\dot V=I_{V0}-I_{V_{Punkt}}t-k\sqrt{\frac{V}{A}}</math> |
|Aktiviert man im Pull-Down-Menü '''Model''' den Befehl '''Equations''' ('''Ctrl+E'''), erscheint das abgebildete Fenster. Setzt man alle Beziehungen in die Bilanzgleichung ein, erhält man die Differentialgleichung <br> <math>\dot V=I_{V0}-I_{V_{Punkt}}t-k\sqrt{\frac{V}{A}}</math> |
||
|[[Bild:Einfaches_Reservoir6.jpg]] |
|[[Bild:Einfaches_Reservoir6.jpg]] |
||
|- |
|- |
||
|'''Daten ausgeben:''' <br> BerkeleyMadonna generiert die |
|'''Daten ausgeben:''' <br> BerkeleyMadonna generiert die graphische Ausgabe der Daten automatisch. Wie kann man die Graphik den eigenen Bedürfnissen anpassen? |
||
| |
|Die Grössen müssen zuerst sortiert werden, weil man nie verschiedene Grössen auf die gleiche Skala bringen sollte. Klickt man zwei Mal ins Diagramm hinein (Doppelklick) geht ein Dialogfenster auf. In diesem Fenster wählt man die Grössen aus, die auf der linken und der rechten ''y''-Skala erscheinen sollen. Zudem kann man die Grösse für die ''x''-Achse auswählen (man muss die verschiedenen Grössen nicht unbedingt gegen die Zeit auftragen). <br> Klickt man auf das schwarze Dreieck in der Kopfleiste, wird eine neue Seite generiert. So lassen sich alle Volumenströme auf der ersten Seite links, das Volumen rechts und die Höhe auf einer zweiten Seite links oder rechts auftragen. Doppelklickt man auf eine Beschriftung der Achse, erscheint ein Diaglogfenster für die Skalaierung und die Beschriftung. Probieren Sie doch einfach alles einmal aus. |
||
|[[Bild:Einfaches_Reservoir7.jpg|300px]] |
|[[Bild:Einfaches_Reservoir7.jpg|300px]] |
||
|} |
|} |
||
'''Zurück zum [[Tutorial|Inhalt]]''' |
|||
[[Kategorie:Modelle]] |
|||
Aktuelle Version vom 24. September 2007, 02:40 Uhr
Wasser strömt mit einer zeitabhängigen Stromstärke in ein Reservoir. Wie verändert sich der Inhalt des Reservoirs? Was passiert, wenn das Reservoir noch ein Leck aufweist? Dieses Problem eignet sich bestens, um in die systemdynamische Modellierungstechnik einzusteigen. Nachfolgend wird gezeigt, wie man diese Aufgabe mit BerkeleyMadonna löst.
Sobald das Programm geöffnet ist, sollten Sie das equations-Fenster wieder schliessen. Öffnen Sie dafür ein flowchart-Fenster (im Pull-Down-Menü File den Befehl New Flowchart auswählen oder mit der Tastenkombination Ctrl+Shift+N). In diesem Fenster, der eigentlichen Modellierungsebene, werden die Modelle als Systemdiagramme aufgebaut. Sollten Sie einmal ein Element zu viel gezeichnet haben, können Sie es mit der Maus aktivieren (erscheint dunkelrot) und mit Ctrl+Delete entfernen.
| Aufgabe | Aktion | Reaktion |
|---|---|---|
| Modellieren: Ein System, bestehend aus Reservoir und Zuleitung, soll modelliert werden. |
Das Modell wird wie folgt erstellt:
|
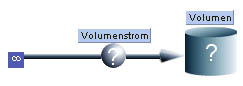 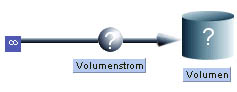
|
| Parametrisieren: Der Eingangsstrom soll sich gemäss folgender Beziehung verändern [math]I_V=I_{V0}-I_{VPunkt}\cdot t[/math] Für die Stärke des Anfangsstroms (I0) können 2 l/s und für die Änderungsrate (IVPunkt) 0.001 l/s2 angenommen werden. Den Inhalt des Reservoirs setze man zum Zeitnullpunkt auf Null. |
Die Parameter Anfangsstrom und Änderungsrate des Stromes bekommen ein eigenes Ikon
|
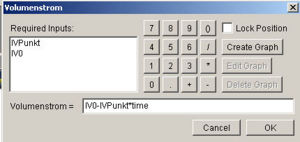 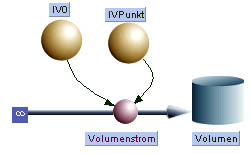
|
| Simulieren: Das Modell, bestehend aus Behälter und einem zeitabhängigen Zufluss, soll nun simuliert werden. Die Simulationszeit betrage 2000 Sekunden und der Zeitschritt kann auf 5 Sekunden gesetzt werden. Als Integrationsmethode verwende man die elementare Euler-Methode. |
Im Pull-Down-Menü Parameters den Befehl Parameter Window (Ctrl+Shift+P)auswählen und entsprechende Zeilen neu setzen bzw. umschreiben 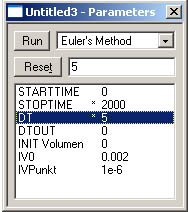 |
Sobald die Taste run im Parameter Window gedrückt wird, geht ein neues Fenster auf 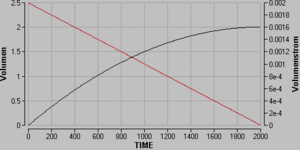
|
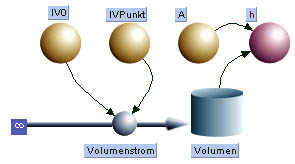
| Erweitern: Das Reservoir sei prismatisch oder zylinderförmig. Der Querschnitt messe 0.4 m2. Das Modell ist so zu erweitern, dass die Füllhöhe angezeigt wird. Was ist zu tun, wenn der Querschnitt als Funktion der Höhe gegeben ist? |
Die Erweiterung sollte nun keine Hexerei mehr sein: Parameter A (formula) für den Querschnitt einführen; Grösse h für die Höhe kreieren; Pfeile von Volumen und Querschnitt zu Höhe ziehen und dort den Quotienten h = Volumen/A bilden. Schwieriger wird die Sache, wenn der Querschnitt eine Funktion der Höhe ist. BerkeleyMadonna lässt keinen zweiten Pfeil von der Höhe zum Querschnitt zu (circular reference). In diesem Fall bleibt nichts anderes übrig, als die Funktion h(V) explizit zu berechnen und dann ins Modell einzufügen. |
|
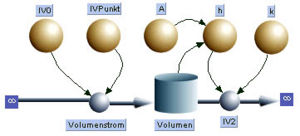
| Rückkoppeln: Das Reservoir leckt. Wie Evangelista Torricelli schon gezeigt hat, fliesst das Wasser gleich schnell aus einem Reservoir aus, wie ein Körper, der von der Wasseroberfläche fallen gelassen wird, am Loch vorbei fliegt. Folglich ist der Leckstrom gleich [math]I_{V2}=A_L \sqrt{2gh}[/math] |
Der Leckstrom ist gleich einer Konstanten k mal die Wurzel aus der Höhe. Die Konstante kann auch als Verhältnis der beiden Grössen geschrieben werden [math]k =\frac {I_{V2}}{\sqrt{h}}[/math] Die Konstante k lässt sich abschätzen. Nimmt man an, dass der Volumenstrom bei einer Füllhöhe von einem Meter ein Liter pro Sekunde beträgt, erhält man für die Konstante k = 0.001 {m2.5/s} |
|
| Analysieren: Das vorliegende Modell wird durch eine Differentialgleichung (nichtlinear, erster Ordnung) beschrieben. Alle Beziehungen, die von BerkeleyMadonna erzeugt werden, sollen nun zu einer einzigen Gleichung zusammengefasst werden. Diese Differentialgleichung beschreibt das dynamische Verhalten ds Systems beschreibt. |
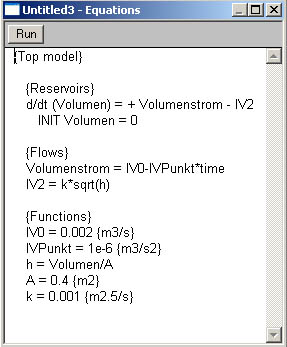
Aktiviert man im Pull-Down-Menü Model den Befehl Equations (Ctrl+E), erscheint das abgebildete Fenster. Setzt man alle Beziehungen in die Bilanzgleichung ein, erhält man die Differentialgleichung [math]\dot V=I_{V0}-I_{V_{Punkt}}t-k\sqrt{\frac{V}{A}}[/math] |
|
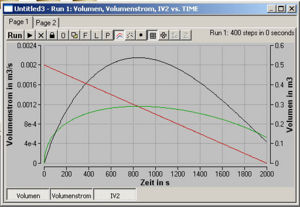
| Daten ausgeben: BerkeleyMadonna generiert die graphische Ausgabe der Daten automatisch. Wie kann man die Graphik den eigenen Bedürfnissen anpassen? |
Die Grössen müssen zuerst sortiert werden, weil man nie verschiedene Grössen auf die gleiche Skala bringen sollte. Klickt man zwei Mal ins Diagramm hinein (Doppelklick) geht ein Dialogfenster auf. In diesem Fenster wählt man die Grössen aus, die auf der linken und der rechten y-Skala erscheinen sollen. Zudem kann man die Grösse für die x-Achse auswählen (man muss die verschiedenen Grössen nicht unbedingt gegen die Zeit auftragen). Klickt man auf das schwarze Dreieck in der Kopfleiste, wird eine neue Seite generiert. So lassen sich alle Volumenströme auf der ersten Seite links, das Volumen rechts und die Höhe auf einer zweiten Seite links oder rechts auftragen. Doppelklickt man auf eine Beschriftung der Achse, erscheint ein Diaglogfenster für die Skalaierung und die Beschriftung. Probieren Sie doch einfach alles einmal aus. |
|
Zurück zum Inhalt