Ölfass u.a. als Speicher: Unterschied zwischen den Versionen

Inhalt hinzugefügt Inhalt gelöscht

Inline

Aktuelle Version vom 14. September 2017, 13:00 Uhr

In einem Schrebergarten wird ein stehendes Ölfass (Volumen 200 l, Höhe 1 m, Füllöffnung beim Fassboden) über eine horizontale Zuleitung durch eine Pumpe mit Wasser gefüllt. Die Pumpe liefert einen konstanten Volumenstrom von 20 l/min.

Berechnen Sie die Speicherkapazität und den Druckverlauf während der Füllzeit. Berechnen Sie auch die für das Füllen benötigte Energie.
Das Fass wird mit einem V-förmigen Gefäss (Volumen 200 l, Höhe 1 m, obere Gefässöffnung 80 cm x 50 cm) ersetzt. Die Füllöffnung befindet sich ebenfalls im tiefsten Punkt. Statt die Speicherkapazität zu berechnen, skizzieren Sie das V-p-Diagramm und bestimmen daraus die benötigte Energie. Sie können auch das I_V-p-t-Schaubild zeichnen und dann die Energie über das Volumen ermitteln. Falls Sie in Ihrer Lösung krummlinig begrenzte Flächen oder Volumen erhalten, nähern Sie diese mit 2 oder 3 Teilen an, die von geraden Linien oder ebenen Flächen begrenzt sind.

Hinweise: Gerades Rohrstück, Gravitationsfeldstärke g = 9.81 N/kg

Hinweise

Resultate

Lösung

Lösungsvideo zu 2

@@ Zeile 1: / Zeile 1: @@
-Eine Pumpe füllt ein stehendes Ölfass (Volumen 200 l, Höhe 1 m, Füllöffnung beim Fassboden) über eine horizontale Zuleitung (Innendurchmesser 6 mm, 10 m Länge). Die Pumpe liefert einen konstanten Volumenstrom von 20 l/min.
+[[Bild:V_Wanne.png|thumb|V-förmiges Gefäss]] In einem Schrebergarten wird ein stehendes Ölfass (Volumen 200 l, Höhe 1 m, Füllöffnung beim Fassboden) über eine horizontale Zuleitung durch eine Pumpe mit Wasser gefüllt. Die Pumpe liefert einen konstanten Volumenstrom von 20 l/min.
 #Berechnen Sie die Speicherkapazität und den Druckverlauf während der Füllzeit. Berechnen Sie auch die für das Füllen benötigte Energie.
-#Das Fass wird mit einem V-förmigen Gefäss (Öffnungswinkel 2 x 14°, Rinnenlänge 1 m) ersetzt. Die Füllöffnung befindet sich ebenfalls im tiefsten Punkt. Berechnen Sie wieder Speicherkapazität, Druckverlauf und benötigte Energie. Falls Sie in Ihrer Lösung Körpervolumen mit gekrümmten Flächen erhalten, nähern Sie diese Volumen mit 2 oder 3 Teilkörpern an, die von ebenen Flächen begrenzt sind.
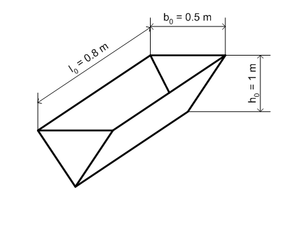
+#Das Fass wird mit einem V-förmigen Gefäss (Volumen 200 l, Höhe 1 m, obere Gefässöffnung 80 cm x 50 cm) ersetzt. Die Füllöffnung befindet sich ebenfalls im tiefsten Punkt. Statt die Speicherkapazität zu berechnen, skizzieren Sie das ''V-p-''Diagramm und bestimmen daraus die benötigte Energie. Sie können auch das ''I<sub>V</sub>-p-t-''Schaubild zeichnen und dann die Energie über das Volumen ermitteln. Falls Sie in Ihrer Lösung krummlinig begrenzte Flächen oder Volumen erhalten, nähern Sie diese mit 2 oder 3 Teilen an, die von geraden Linien oder ebenen Flächen begrenzt sind.
-'''Hinweis''': [[Gerades Rohrstück]]
+'''Hinweise''': [[Gerades Rohrstück]], Gravitationsfeldstärke g = 9.81 N/kg
+'''[[Hinweise zu Ölfass u.a. als Speicher|Hinweise]]'''
+'''[[Resultate zu Ölfass u.a. als Speicher|Resultate]]'''
 '''[[Lösung zu Ölfass u.a. als Speicher|Lösung]]'''
+'''[http://youtu.be/gUP5i52pbz0 Lösungsvideo zu 2]'''
 [[Kategorie: Hydro]] [[Kategorie: Aufgaben]]  [[Kategorie: HydroAuf]]  [[Kategorie: UebAV]]