Bananenflanke: Unterschied zwischen den Versionen

Inhalt hinzugefügt Inhalt gelöscht

Inline

Aktuelle Version vom 8. Juli 2008, 06:07 Uhr

Eine Bananenflanke ist ein Querpass des Fussballs vor das gegnerische Tor mit stark gekrümmter Flugbahn. Dazu muss der Ball aus dem Spiel heraus mit Effet getreten werden. Durch die unerwartete Bahn des Balls wird der Gegner häufig überrascht. Um eine Bananenflanke zu erzeugen, wird der Ball durch einen Innenspannstoss getreten. Dabei "wischt" der ausführende Fuss mit seiner Innenseite am Ball vorbei und sorgt so für eine seitliche Rotation des Balls.

Kräfte

Bei der Bananenflanke tauschen das Gravitationsfeld und die umgebende Luft Impuls mit dem Ball aus. Die durch das Gravitationsfeld im Ball erzeugte Impulsquelle nennt man Gewichtskraft. Die Einwirkung der Luft kann in einen Luftwiderstand und eine Magnuskraft zerlegt werden. Der Luftwiderstand wirkt in Richtung der Anströmung, also gegen die Geschwindigkeit des Balls. Die Magnuskraft steht normal zur Anströmung und normal zum Vektor der Winkelgeschwindigkeit.

Modellbildung

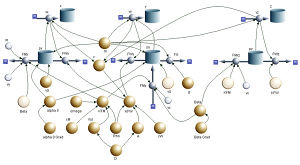
Die Bananenflanke lässt sich mit Hilfe der systemdynamischen Werkzeuge recht einfach simulieren. Dazu formuliert man drei Impulsbilanzen und drei Orts-Integratoren (für jede der drei Raumdimensionen je eine Impulsbilanz und eine Ortsberechnung). Die drei Achsen des rechthändigen Koordinatensystems werden so gewählt, dass die Gesetze und Anfangsbedingungen eine möglichst einfache Gestalt annehmen:

x-Achse horizontal in Abschussrichtung
y-Achse vertikal nach oben
z-Achse horizontal und normal zur Abschussrichtung

Die Gewichtskraft wird als konstante Impulssenke modelliert (das Gravitationsfeld entzieht dem Ball mit konstanter Rate Impuls)

[math]\vec F_G=m\vec g[/math]

Die Wirkung der Luft wird in einen Luftwiderstand

[math]\vec F_W=\frac \varrho 2 c_W Av\vec v[/math]

und eine Magnuskraft zerlegt

[math]\vec F_M=2\rho c_M V(\vec \omega\times \vec v)[/math]

Die beiden Formfaktoren oder Beiwerte c_W und c_M lassen sich näherungsweise mit Hilfe von CFD-Simulationen oder experimentell (Messungen im Windkanal oder Vermessung der Flugbahn) bestimmen. Die Verringerung der Winkelgeschwindigkeit infolge der Reibung (Abgabe von Drehimpuls an die Luft) ist vernachlässigbar.

Simulation

Die unten stehenden Bilder zeigen die Gleichungen sowie die verschiedenen Bahnen des Balls von oben gesehen. Die Winkelgeschwindigkeiten variiert in zwei Schritten von plus 60 s^-1 bis minus 60 s^-1 (entsprechend plus minus 10 Umdrehungen pro Sekunde). Der Abschuss erfolgt mit 108 km/h unter einem Winkel von 25°. Für die Widerstandszahl c_W ist hier 0.2 und für die Magnuszahl c_M 0.15 eingesetzt worden.

Gleichungen
Bahn: y und z gegen x

Weblinks

www.weltderphysik.de - Wieso ist die Bananenflanke krumm?

@@ Zeile 1: / Zeile 1: @@
-Eine '''Bananenflanke''' ist ein Querpass des [[Fussall]]s vor das gegnerische Tor mit stark gekrümmter Flugbahn. Dafür wird der Ball aus dem Spiel heraus mit [[Effet]] getreten. Durch die unerwartete Bahn des Balls wird der Gegner häufig überrascht. Technisch erreicht wird die Bananenflanke durch den so genannten Innenspannstoss. Dabei "wischt" der ausführende Fuss mit seiner Innenseite am Ball vorbei und sorgt so für eine seitliche Rotation des Balls.
+Eine '''Bananenflanke''' ist ein Querpass des [[Fussball]]s vor das gegnerische Tor mit stark gekrümmter Flugbahn. Dazu muss der Ball aus dem Spiel heraus mit [[Effet]] getreten werden. Durch die unerwartete Bahn des Balls wird der Gegner häufig überrascht. Um eine Bananenflanke zu erzeugen, wird der Ball durch einen Innenspannstoss getreten. Dabei "wischt" der ausführende Fuss mit seiner Innenseite am Ball vorbei und sorgt so für eine seitliche Rotation des Balls.
 ==Kräfte==
@@ Zeile 5: / Zeile 5: @@
 ==Modellbildung==
-[[Bild:Fussball_3_SD.jpg|thumb|Systemdiagramm (flowchart]] Die Bananenflanke lässt sich mit Hilfe der [[System Dynamics|systemdynamischen Werkzeuge]] recht einfach simulieren. Dazu formuliert man drei Impulsbilanzen und drei Orts-Integratoren (also für jede der drei Raumdimensionen je eine Impulsbilanz und eine Ortsberechnung). Die drei Achsen des [[rechte-Hand-Regel|rechthändigen]] Koordinatensystems werden so gewählt, dass die Gesetze und Anfangsbedingungen eine möglichst einfache Gestalt annehmen:
+[[Bild:Fussball_3_SD.jpg|thumb|Systemdiagramm (flowchart]] Die Bananenflanke lässt sich mit Hilfe der [[System Dynamics|systemdynamischen Werkzeuge]] recht einfach simulieren. Dazu formuliert man drei [[Impulsbilanz]]en und drei Orts-Integratoren (für jede der drei Raumdimensionen je eine Impulsbilanz und eine Ortsberechnung). Die drei Achsen des [[rechte-Hand-Regel|rechthändigen]] Koordinatensystems werden so gewählt, dass die Gesetze und Anfangsbedingungen eine möglichst einfache Gestalt annehmen:
 *''x-''Achse horizontal in Abschussrichtung
 *''y-''Achse vertikal nach oben
-*''z-''Achse horizontal normal zur Abschussrichtung
+*''z-''Achse horizontal und normal zur Abschussrichtung
-Die Gewichtskraft wird als konstante Impulsstromsenke modelliert (das Gravitationsfeld entzieht dem Ball mit konstanter Rate Impuls)
+Die Gewichtskraft wird als konstante Impulssenke modelliert (das Gravitationsfeld entzieht dem Ball mit konstanter Rate Impuls)
 :<math>\vec F_G=m\vec g</math>
 Die Wirkung der Luft wird in einen [[Luftwiderstand]]
+:<math>\vec F_W=\frac \varrho 2 c_W Av\vec v</math>
 und eine [[Magnus-Effekt|Magnuskraft]] zerlegt
+:<math>\vec F_M=2\rho c_M V(\vec \omega\times \vec v)</math>
-Die Verringerung der [[Winkelgeschwindigkeit]] infolge der Reibung (Abgabe von [[Drehimpuls]] an die Luft) kann man vernachlässigen.
+Die beiden Formfaktoren oder Beiwerte ''c<sub>W</sub>'' und ''c<sub>M</sub>'' lassen sich näherungsweise mit Hilfe von [[CFD]]-Simulationen oder experimentell (Messungen im Windkanal oder Vermessung der Flugbahn)  bestimmen. Die Verringerung der [[Winkelgeschwindigkeit]] infolge der Reibung (Abgabe von [[Drehimpuls]] an die Luft) ist vernachlässigbar.
 ==Simulation==
-Die unten stehenden Bilder zeigen das Systemdiagramm, die Gleichungen sowie die verschiedenen Bahnen des Balls von oben gesehen. Die Winkelgeschwindigkeiten variiert von plus 60 s<sup>-1</sup> bis minus 60 s<sup>-1</sup> (entsprechend plus minus 10 Umdrehungen pro Sekunde). Der Abschuss erfolgt mit 108 km/h unter einem Winkel von 45°.
+Die unten stehenden Bilder zeigen die Gleichungen sowie die verschiedenen Bahnen des Balls von oben gesehen. Die Winkelgeschwindigkeiten variiert in zwei Schritten von plus 60 s<sup>-1</sup> bis minus 60 s<sup>-1</sup> (entsprechend plus minus 10 Umdrehungen pro Sekunde). Der Abschuss erfolgt mit 108 km/h unter einem Winkel von 25°. Für die Widerstandszahl ''c<sub>W</sub>'' ist hier 0.2 und für die Magnuszahl ''c<sub>M</sub>'' 0.15 eingesetzt worden.
 <gallery>
  Bild:Fussball_3_Gl.png|Gleichungen