Lösung zu Ölfass u.a. als Speicher: Unterschied zwischen den Versionen

Inhalt hinzugefügt Inhalt gelöscht

Inline

Aktuelle Version vom 13. Oktober 2009, 13:11 Uhr

1. Ölfass

Ein Gefäss mit senkrechten Wänden ist ein linearer Speicher. Deshalb ist die Kapazität gleich

[math]C_V = \frac {\Delta V} {\Delta p} = \frac {V_0} {\rho * g * h_0} = \frac {0.2 m^3} {1000 kg/m^3 * 9.81 N/kg * 1 m} = 2.04 * 10^{-5} m^3/Pa [/math]

Der Druck (Überdruck relativ zum Umgebungsdruck) steigt während der Füllzeit t_F = V₀ / I_V = 10 min linear von 0 auf 0.098 bar an.

Die Energie ist gleich

[math]W = \frac {V_0^2} {2 C_V} = 980 J [/math]

2. V-förmiges Gefäss (Rinne)

Wir erhalten das V(p)-Diagramm, wenn wir Druck und Volumen in Abhängigkeit der momentanen Füllhöhe berechnen:

[math] p = \rho \cdot g \cdot h, \quad V = \frac {1} {2} \cdot b \cdot h \cdot l_0 [/math]

Die Dreiecke auf einer Seitenwand sind zueinander ähnlich. Deshalb gilt:

[math] \quad b / h = b_0 / h_0, \quad b = b_0 \cdot \frac {h} {h_0} [/math]

Wir setzen dies in die Formel für V ein und erweitern den Quotienten mit h₀:

[math] V = \frac {1} {2} \cdot b_0 \cdot \frac {h} {h_0} \cdot h \cdot l_0 = \frac {1} {2} \cdot b_0 \cdot \frac {h \cdot h_0 } {h_0^2} \cdot h \cdot l_0 = \frac {1} {2} \cdot b_0 \cdot h_0 \cdot l_0 \cdot \frac {h^2 } {h_0^2} [/math]

Mit

[math] V_0 = \frac {1} {2} \cdot b_0 \cdot h_0 \cdot l_0 \quad [/math]

erhalten wir

[math] V = V_0 \cdot(\frac {h} {h_0})^2[/math]

b ist proportional zu h, deshalb ist V proportional zu h² und auch zu p², weil ja p proportional zu h ist. Der Graph dieser Funktion ist eine nach oben geöffnete Parabelkurve durch den Nullpunkt (nichtlinearer Speicher), wobei p₀ = 9.81 kPa der Druck für das volle Gefäss ist:

[math]V = V_0 * (\frac {p} {p_0})^2[/math]

Um den Druckverlauf p(t) zu erhalten, lösen wir die Funktion V(p) nach p auf und setzen für V den Ausdruck I_V * t ein. Hier ist ja I_V konstant, deshalb nimmt das Volumen linear in der Zeit zu. Wir erhalten wieder eine Parabel, aber diesmal nach rechts geöffnet:

[math]p = p_0 * \sqrt {\frac{I_v * t} {V_0}} = p_0 * \sqrt {\frac{t} {t_F}} = 9.81 kPa * \sqrt {\frac{t} {600 s}} [/math]

Für die Berechnung der Energie brauchen wir das p(V)-Diagramm, also ein Diagramm mit dem Druck als Funktion des Volumens. Dazu vertauschen wir die Achsen des V(p)-Diagramms von oben: Wir erhalten hier auch eine Parabel, sie ist auch nach rechts geöffnet: [math]p = p_0 * \sqrt {\frac{V} {V_0}}[/math]. Die Fläche unter der Kurve approximieren wir mit 2 gleich breiten "Pommes Frites". Dafür brauchen wir den Druck bei halbem Volumen: p₅₀ = 6.94 kPa. Die mittleren Drucke beider Pommes Frites betragen dann:

für das erste (0 + 6.94 kPa)/2 = 3.5 kPa,

für das zweite (6.94 kPa + 9.81 kPa)/2 = 8.4 kPa.

Nun können wir die Fläche der Pommes berechnen:

W = 3.5 kPa * 0.1 m3 + 8.4 kPa * 0.1 m3 = 1.2 kJ.

Bei der Berechnung der Energie könnte man auch direkt das V(p)-Diagramm verwenden. Man müsste aber die Fläche rechts von der Kurve berechnen.

Aufgabe

@@ Zeile 3: / Zeile 3: @@
 Ein Gefäss mit senkrechten Wänden ist ein linearer Speicher. Deshalb ist die Kapazität gleich
-:<math>C_V = \frac {A} {\rho * g} = \frac {V_0} {\rho * g * h_0} = 2 * 10^{-5} m^3/Pa </math>
+:<math>C_V = \frac {\Delta V} {\Delta p} = \frac {V_0} {\rho * g * h_0} = \frac {0.2 m^3} {1000 kg/m^3 * 9.81 N/kg * 1 m} = 2.04 * 10^{-5} m^3/Pa </math>
-Der Druck gegen den Umgebungsdruck steigt während der Füllzeit t<sub>F</sub> = V<sub>0</sub> / I<sub>V</sub> = 10 min linear von 0 auf 0.1 bar an.
+Der Druck (Überdruck relativ zum Umgebungsdruck) steigt während der Füllzeit t<sub>F</sub> = V<sub>0</sub> / I<sub>V</sub> = 10 min linear von 0 auf 0.098 bar an.
 Die Energie ist gleich
-:<math>W = \frac {V_{end}^2} {2 C_V} = 1000 J </math>
+:<math>W = \frac {V_0^2} {2 C_V} = 980 J </math>
 ==2. V-förmiges Gefäss (Rinne)==
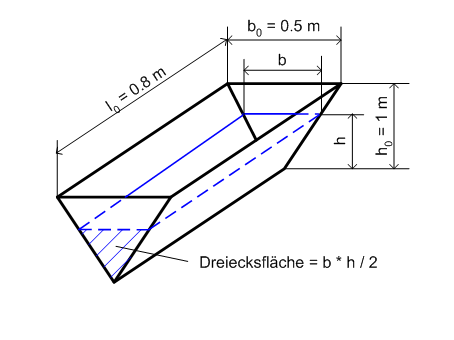
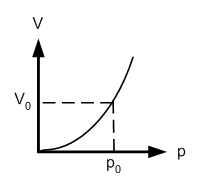
-[[Bild:V_Wanne_2.png|thumb|Volumenberechnung für die V-förmige Wanne]][[Bild:Graph_von_V_Wanne.png|thumb|V/p-Diagramm einer V-förmigen Wanne]] Wir erhalten das ''V-p-''Diagramm, wenn wir Druck und Volumen in Abhängigkeit der momentanen Füllhöhe berechnen:
+[[Bild:V_Wanne_2.png|Volumenberechnung für die V-förmige Wanne]][[Bild:Graph_von_V_Wanne.png|V/p-Diagramm einer V-förmigen Wanne]]
+Wir erhalten das ''V(p)-''Diagramm, wenn wir Druck und Volumen in Abhängigkeit der momentanen Füllhöhe berechnen:
-:<math>p = \rho * g * h, \quad V = \frac {1} {2} * A * h = V_0 *(\frac {h} {h_0})^2</math>
+:<math> p = \rho \cdot g \cdot h, \quad V = \frac {1} {2} \cdot b \cdot h \cdot l_0 </math>
-A ist proportional zu h, deshalb ist V proportional zu h<sup>2</sup>.
+Die Dreiecke auf einer Seitenwand sind zueinander ähnlich. Deshalb gilt:
-Der Graph dieser Funktion ist eine nach oben geöffnete Parabelkurve durch den Nullpunkt (nichtlinearer Speicher)
+:<math> \quad b / h = b_0 / h_0, \quad b  = b_0 \cdot \frac {h} {h_0}  </math>
+Wir setzen dies in die Formel für V ein und erweitern den Quotienten mit h<sub>0</sub>:
+: <math> V = \frac {1} {2} \cdot b_0 \cdot \frac {h} {h_0} \cdot h \cdot l_0 = \frac {1} {2} \cdot b_0 \cdot \frac {h \cdot h_0 } {h_0^2} \cdot h \cdot l_0  = \frac {1} {2} \cdot b_0 \cdot h_0 \cdot l_0 \cdot \frac {h^2 } {h_0^2} </math>
+Mit
+:<math> V_0 = \frac {1} {2} \cdot b_0 \cdot h_0 \cdot l_0 \quad </math>
+erhalten wir
+:<math> V = V_0 \cdot(\frac {h} {h_0})^2</math>
+b ist proportional zu h, deshalb ist V proportional zu h<sup>2</sup> und auch zu p<sup>2</sup>, weil ja p proportional zu h ist. Der Graph dieser Funktion ist eine nach oben geöffnete Parabelkurve durch den Nullpunkt (nichtlinearer Speicher), wobei p<sub>0</sub> = 9.81 kPa der Druck für das volle Gefäss ist:
 :<math>V = V_0 * (\frac {p} {p_0})^2</math>
-Um den Druckverlauf ''p(t)'' zu erhalten, lösen wir die Funktion ''V(p'') nach ''p'' auf und setzen für ''V'' den Ausdruck I<sub>V</sub> * t ein. Wir erhalten wieder eine Parabel, aber diesmal nach rechts geöffnet
+Um den Druckverlauf ''p(t)'' zu erhalten, lösen wir die Funktion ''V(p'') nach ''p'' auf und setzen für ''V'' den Ausdruck I<sub>V</sub> * t ein. Hier ist ja I<sub>V</sub> konstant, deshalb nimmt das Volumen linear in der Zeit zu. Wir erhalten wieder eine Parabel, aber diesmal nach rechts geöffnet:
+:<math>p = p_0 * \sqrt {\frac{I_v * t} {V_0}} = p_0 * \sqrt {\frac{t} {t_F}} = 9.81 kPa * \sqrt {\frac{t} {600 s}} </math>
+Für die Berechnung der Energie brauchen wir das ''p(V)''-Diagramm, also ein Diagramm mit dem Druck als Funktion des Volumens. Dazu vertauschen wir die Achsen des ''V(p)''-Diagramms von oben: Wir erhalten hier auch eine Parabel, sie ist auch nach rechts geöffnet: <math>p = p_0 * \sqrt {\frac{V} {V_0}}</math>. Die Fläche unter der Kurve approximieren wir mit 2 gleich breiten "Pommes Frites". Dafür brauchen wir den Druck bei halbem Volumen: p<sub>50</sub> = 6.94 kPa. Die mittleren Drucke beider Pommes Frites betragen dann:
+:für das erste (0 + 6.94 kPa)/2 = 3.5 kPa,
-:<math>p = p_0 * \sqrt {\frac{I_v * t} {V_0}} = p_0 * \sqrt {\frac{t} {t_F}} </math>
+:für das zweite (6.94 kPa + 9.81 kPa)/2 = 8.4 kPa.
-Die Energie berechnen wir im ''p-V-''Diagramm, das ist das ''V-p-''Diagramm von oben aber mit vertauschten Achsen: Hier erhalten wir auch eine nach rechts geöffnete Parabel: <math>p = p_0 * \sqrt {\frac{V} {V_0}}</math>
+Nun können wir die Fläche der Pommes berechnen:
-Die Fläche unter der Kurve approximieren wir mit 2 gleich breiten "Pommes Frites". Dafür brauchen wir den Druck bei halbem Volumen: p<sub>50</sub> = 7.1 kPa. Die mittleren Drucke beider Pommes Frites betragen dann 3.5 kPa, bzw. 8.5 kPa. Nun können wir die Fläche der Pommes berechnen:
-:W = 3.5 kPa * 0.1 m3 + 8.5 kPa * 0.1 m3 = 1200 J.
+:W = 3.5 kPa * 0.1 m3 + 8.4 kPa * 0.1 m3 = 1.2 kJ.
+Bei der Berechnung der Energie könnte man auch direkt das ''V(p)''-Diagramm verwenden. Man müsste aber die Fläche '''''rechts''''' von der Kurve berechnen.