Lösung zu Aviatik 2008/4: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
|||
| (5 dazwischenliegende Versionen von einem anderen Benutzer werden nicht angezeigt) | |||
| Zeile 14: | Zeile 14: | ||
==Aufgabe 3== |
==Aufgabe 3== |
||
Diese Aufgabe schreit förmlich nach dem [[Flüssigkeitsbild]]. Das Antriebssystem entzieht dem einen "Rad" [[Drehimpuls]] mit einer Stromstärke von 4.4 kNm und pumpt diesen in das andere "Rad". Beim Bremsen fliesst der Drehimpuls zurück. |
|||
Eine Raumstation hat die Form von zwei Tori (Donuts), d.h. die Raumstation sieht aus wie ein kleines und ein grosses Rad, die um eine gemeinsame Achse drehen. Der grosse Torus hat einen Aussendurchmesser von 50 m. Um den Bewohnern ein Leben wie auf der Erdoberfläche zu ermöglichen, werden die beiden „Räder“ in gegenläufige Rotation versetzt. Nach einer zehnstündigen Beschleunigungsphase mit einem [[Drehimpulsstrom]] der Stärke 4.4 kNm dreht sich das grosse Rad alle zehn Sekunden und das kleine alle sechs Sekunden einmal um die eigene Achse. |
|||
#Der total gepumpte Drehimpuls ist gleich Stromstärke mal Zeit. Nun kennt man auch noch die [[Winkelgeschwindigkeit]]en (Füllhöhen) am Schluss des Prozesses (0.628 1/s und -1.05 1/s). Folglich sind die beiden Massenträgheitsmomente (Inhalt durch Füllhöhe) gleich 2.52 10<sup>8</sup> kgm<sup>2</sup> und 1.51 10<sup>8</sup> kgm<sup>2</sup>. |
|||
#Wie gross sind die [[Massenträgheitsmoment]]e der beiden Teile der Raumstation? |
|||
#Die [[Prozessleistung]] ist immer gleich Stromstärke mal Pumphöhe, also gleich Drehmoment (Drehimpulsstrom) mal momentane Winkelgeschwindigkeit <math>P=\Delta\omega I_L</math> = 4.4 kNm * 0.838 1/s = 3.69 kW. |
|||
#Welche Leistung gibt das Antriebssystem nach der halben Beschleunigungsphase ab? |
|||
#Im Bremsvorgang fällt die Hälfte des gespeicherten Drehimpulses (0.5*1.58 10<sup>8</sup> Nms) in 30 Minuten im Mittel über 75% der maximalen Differenz der Winkelgeschwindigkeiten. Dies ergibt einen Strom von 44 kNm und eine freigesetzte Energie von 99.5 MJ. |
|||
#Das Bremssystem muss die Drehzahl in 30 Minuten vom Normwert (Umlaufzeit 10 s bzw. 6 s) auf die Hälfte absenken können. Wie stark ist bei diesem Vorgang der mittlere [[Drehimpulsstrom]]? Wie viel Energie wird dabei vom Bremssystem umgesetzt? |
|||
#In einem rotierenden System tritt ein zusätzliches Gravitationsfeld ([[Zentrifugalfeld]]) auf, dessen Stärke gleich <math>g_z=\omega^2r</math> ist. Mit dieser Formel erhält man für das grosse Rad eine Feldstärke von 9.87 N/kg und für das kleine einen Durchmesser von 18 m. |
|||
#Wie stark ist das [[Zentrifugalfeld]] an der Peripherie (beim Aussenradius) des grossen Torus im Normalbetrieb? Welchen Durchmesser muss der kleine Torus aufweisen, damit die Feldstärke an dessen Peripherie den gleichen Wert aufweist? |
|||
==Aufgabe 4== |
==Aufgabe 4== |
||
Diese Aufgabe orientiert sich an der Problemstellung [[Kinematik des Bugrades]]. |
|||
Ein landendes Flugzeug bewegt sich zu einem bestimmten Zeitpunkt mit einer Geschwindigkeit von 72 km/h über die Piste. Im gleichen Moment dreht sich das Bugrad (Durchmesser 0.8 m) mit 48 U/min und erfährt eine [[Winkelbeschleunigung]] von 5 s-2. Das Flugzeug und somit auch die Achse des Bugrades werden mit -2 m/s<sup>2</sup> abgebremst. |
|||
#<math>v_1=v_0-\omega r</math> = 18 m/s. |
|||
#Welche [[Geschwindigkeit]] hat im fraglichen Moment der unterste Teil des Rades? |
|||
#Die Normalbeschleunigung auf einer rotierenden Scheibe ist gleich <math>a_n=\omega^2r</math> = 10.11 m/s<sup>2</sup> und die Tangentialbeschleunigung gleich <math>a_t=\alpha r</math> = 2 m/s<sup>2</sup>. Zählt man diese Teilbeschleunigungen vektoriell mit der Beschleunigung der Achse zusammen, erhält man einen Wert von 10.87 m/s<sup>2</sup>. |
|||
#Welche Beschleunigung erfährt dann dieser Teil des Rades? |
|||
#Mit einer zu Teilaufgabe 2 analogen Lösung findet man den Wert 12.27 m/s<sup>2</sup>. |
|||
#Wie gross ist dann Beschleunigung des vordersten Teiles des Rades? |
|||
#Aus der Rollbedingung <math>v_0-\omega r=0</math> folgt für die Winkelgeschwindigkeit ''ω'' = 50 1/s (477.5 U/min). |
|||
#Wie schnell müsste sich das Bugrad drehen, damit es auf der Piste abrollt? |
|||
==Aufgabe 5== |
==Aufgabe 5== |
||
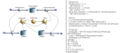
Als Basismodell nimmt man am besten den [[Carnotor]]. Doch statt über eine Verdrängerflüssigkeit das Volumen zu beeinflussen kann nun direkt die Volumenänderung modelliert werden. Dabei ist zu beachten, dass bei der Kompression die Volumenänderungsrate kleiner Null wird. Folglich sind die Bezugsrichtungen für die ¨Volumenänderungsrate und den mechanischen Energiestrom gegeneinander gerichtet. Die nachfolgenden Bilder zeigen das Modell mit den Gleichungen sowie die beiden Diagramme |
|||
Der Arbeitszyklus eines Benzinmotors kann durch die Abfolge von 4 Iso-Schritten idealisiert werden: |
|||
#[[isentrop]]: Verdichten |
|||
<gallery> |
|||
#[[isochor]]: Verbrennen |
|||
Bild:Aviatik 08 4 L50.jpg|Systemdiagramm und Gleichungen |
|||
#[[isentrop]]: Expansion |
|||
Bild:Aviatik 08 4 L52.png|''T-S-''Diagramm |
|||
#[[isochor]]: Ausstossen und neue Luft ansaugen |
|||
Bild:Aviatik 08 4 L53.png|''p-V-''Diagramm |
|||
Modellieren Sie den 1. (Teilaufgabe 2) und den 2. Schritt (Teilaufgabe 3) mit [[Entropiebilanz|Entropie-]], [[Volumenbilanz|Volumen-]] und Innere [[Energiebilanz]] in einem Zylinder des Motors. Beim Verdichten wird das Maximalvolumen von 0.5 Liter auf 10% komprimiert. Der 1. Schritt soll 10 ms, der 2. Schritt 2 ms dauern. Beim Verbrennungsschritt wird eine Energie von 400 J zugeführt. |
|||
</gallery> |
|||
#Zeichnen Sie zuerst ein qualitatives p-V- und T-S-Diagramm der ersten beiden Schritte. |
|||
#Skizzieren Sie das [[Systemdiagramm]] (flowchart) für den 1. Schritt des Benzinmotorzyklus. Schreiben Sie die zur Berechnung notwendigen Gleichungen nicht ins Systemdiagramm hinein, sondern auf einer separaten Liste daneben oder unterhalb. |
|||
'''[[Aviatik 2008/4|Aufgabe]]''' |
|||
#Skizzieren Sie das [[Systemdiagramm]] (flowchart) für den 2. Schritt zu diesem Modell (Entropie-, Volumen- und Innere Energiebilanz). Schreiben Sie die zur Berechnung notwendigen Gleichungen nicht ins Systemdiagramm hinein, sondern auf einer separaten Liste daneben oder unterhalb. Falls dieses Flowchart fast gleich aussieht wie das erste, können Sie die abweichenden Symbole und Pfeile auch mit einer anderen Farbe unter 2. eintragen. |
|||
Aktuelle Version vom 6. Juli 2009, 14:00 Uhr
Aufgabe 1
Die Wärmepumpe muss die Entropie, die andauernd von aussen in die Truhe eindringt, weg pumpen. Beim Hineinfliessen vermehrt sich die Entropie und die Energie bleibt erhalten.
- Eines der grundlegendsten Gesetze der Systemphysik besagt, dass die aufzuwendende Energie gleich Menge mal Pumphöhe ist. Hier ist die Menge die Entropie und die Pumphöhe die Temperaturdifferenz. Demnach gilt [math]S_{gepumpt}=\frac{W}{\Delta T}=\frac{4.32 MJ}{70 K}[/math] = 61.7 kJ/K.
- Der durch die Wärmepumpe fliessende Entropiestrom hat die Stärke [math]I_S=\frac{P}{\Delta T}[/math] = 0.714 W/K. Folglich hat der in die Wärmepumpe hinein fliessende Entropiestrom eine Stärke von [math]I_W=T_{unten}I_S[/math] = 171 W. Damit sich in der Truhe nichts ändert, muss der in die Kühltruhe hinein fliessende Energiestrom auch gleich 171 W sein.
- Der thermische Leitwert ist gleich [math]G_W=\frac{I_W}{\Delta T_2}[/math] = 4.51 W/K
- Im System Kühltruhe ändert sich nichts. Folglich wird der Umgebung netto die vom elektrischen Strom frei gesetzte Energie in Form von Wärme zugeführt, d.h. die insgesamt produzierte Entropie trägt diese Energie nach aussen weg: [math]S_{erz}=\Delta S_{Umgebung}=\frac{\Delta W_{Umgebung}}{T_{Umgebung}}=\frac{W_{el}}{T_{Umgebung}}[/math] = 14.7 kJ/.
Aufgabe 2
Die vier Grundprozesse (isochor, isobar, isentrop und isotherm) verlaufen entweder im T-S- oder im p-V-Diagramm entlang von Koordinatenlinien. Elementare Kreisprozesse werden aus diesen vier Grundprozessen zusammen gesetzt.
- Für die Teilprozesse siehe ideales Gas.
- Nach den isochoren Heizen ist der Druck gleich [math]p_2=p_1\frac{T_2}{T_1}[/math] = 30 bar. Nach der isentropen Expansion vergrössert sich das Volumen auf [math]V_3=V_2\left(\frac{p_2}{p_3}\right)^\frac{1}{\kappa}[/math] = 133.6 Liter
- Für die thermisch zugeführte Energie gilt [math]W_{therm}=\Delta W=n\hat c_V\Delta T=\frac 52\frac{p_1V_1}{T_1}\Delta T[/math] = 250 kJ. Die zugeführte Entropie entspricht der Zunahme im Gas: [math]S=n\hat c_V\ln\left(\frac{T_1}{T_2}\right)[/math] = 675.8 J/K.
- Nach dem ganzen Kreisprozess ist die mechanische abgeführte Energie gleich der thermisch zugeführten. Diese Energie ist in beiden Diagrammen als ausgeschnittene Fläche zu erkennen. Nun kann man den totalen Energieaustausch sowohl auf der thermischen als auch auf der mechanischen Seite rechnen. Nimmt man die thermische Seite, gilt [math]W_{Nutz}=W_{therm_1}+W_{therm_2}=n\left(\hat c_V\Delta T_{12}+\hat c_p\Delta T_{31}\right)[/math] = 14.8 kJ. Die Anfangstemperatur für den dritten Teilprozess beträgt [math]T_3=T_1\frac{V_3}{V_1}[/math] = 400.7 K.
Aufgabe 3
Diese Aufgabe schreit förmlich nach dem Flüssigkeitsbild. Das Antriebssystem entzieht dem einen "Rad" Drehimpuls mit einer Stromstärke von 4.4 kNm und pumpt diesen in das andere "Rad". Beim Bremsen fliesst der Drehimpuls zurück.
- Der total gepumpte Drehimpuls ist gleich Stromstärke mal Zeit. Nun kennt man auch noch die Winkelgeschwindigkeiten (Füllhöhen) am Schluss des Prozesses (0.628 1/s und -1.05 1/s). Folglich sind die beiden Massenträgheitsmomente (Inhalt durch Füllhöhe) gleich 2.52 108 kgm2 und 1.51 108 kgm2.
- Die Prozessleistung ist immer gleich Stromstärke mal Pumphöhe, also gleich Drehmoment (Drehimpulsstrom) mal momentane Winkelgeschwindigkeit [math]P=\Delta\omega I_L[/math] = 4.4 kNm * 0.838 1/s = 3.69 kW.
- Im Bremsvorgang fällt die Hälfte des gespeicherten Drehimpulses (0.5*1.58 108 Nms) in 30 Minuten im Mittel über 75% der maximalen Differenz der Winkelgeschwindigkeiten. Dies ergibt einen Strom von 44 kNm und eine freigesetzte Energie von 99.5 MJ.
- In einem rotierenden System tritt ein zusätzliches Gravitationsfeld (Zentrifugalfeld) auf, dessen Stärke gleich [math]g_z=\omega^2r[/math] ist. Mit dieser Formel erhält man für das grosse Rad eine Feldstärke von 9.87 N/kg und für das kleine einen Durchmesser von 18 m.
Aufgabe 4
Diese Aufgabe orientiert sich an der Problemstellung Kinematik des Bugrades.
- [math]v_1=v_0-\omega r[/math] = 18 m/s.
- Die Normalbeschleunigung auf einer rotierenden Scheibe ist gleich [math]a_n=\omega^2r[/math] = 10.11 m/s2 und die Tangentialbeschleunigung gleich [math]a_t=\alpha r[/math] = 2 m/s2. Zählt man diese Teilbeschleunigungen vektoriell mit der Beschleunigung der Achse zusammen, erhält man einen Wert von 10.87 m/s2.
- Mit einer zu Teilaufgabe 2 analogen Lösung findet man den Wert 12.27 m/s2.
- Aus der Rollbedingung [math]v_0-\omega r=0[/math] folgt für die Winkelgeschwindigkeit ω = 50 1/s (477.5 U/min).
Aufgabe 5
Als Basismodell nimmt man am besten den Carnotor. Doch statt über eine Verdrängerflüssigkeit das Volumen zu beeinflussen kann nun direkt die Volumenänderung modelliert werden. Dabei ist zu beachten, dass bei der Kompression die Volumenänderungsrate kleiner Null wird. Folglich sind die Bezugsrichtungen für die ¨Volumenänderungsrate und den mechanischen Energiestrom gegeneinander gerichtet. Die nachfolgenden Bilder zeigen das Modell mit den Gleichungen sowie die beiden Diagramme
-
Systemdiagramm und Gleichungen
-
T-S-Diagramm
-
p-V-Diagramm