DGL aus Berkeley Madonna: Unterschied zwischen den Versionen
Inhalt hinzugefügt Inhalt gelöscht
(Die Seite wurde neu angelegt: «In der Vorlesung haben Sie das Berkeley-Madonna Modell zum Abkühlen einer Bierflasche kennengelernt. Die Abbildung zeigt das Flowchart dieses Modells. Die z…») |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
In der Vorlesung haben Sie das Berkeley-Madonna Modell zum Abkühlen einer Bierflasche kennengelernt. Die Abbildung zeigt das [[Flowchart]] dieses Modells. Die zugehörigen Gleichungen lauten |
[[Datei:BierflascheBM.jpg|thumb|Flowchart zur Bierflasche]]In der Vorlesung haben Sie das Berkeley-Madonna Modell zum Abkühlen einer Bierflasche kennengelernt. Die Abbildung zeigt das [[Flowchart]] dieses Modells. Die zugehörigen Gleichungen lauten |
||
<code>{Top model} |
<code>{Top model} |
||
{Reservoirs} |
{Reservoirs} |
||
| Zeile 17: | Zeile 17: | ||
#Verwenden Sie die Anfangsbedingung, um die unbestimmte Konstante in der Lösung der DGL zu bestimmen. Formulieren Sie die vollständige DGL mit allen bekannten Zahlenwerten. |
#Verwenden Sie die Anfangsbedingung, um die unbestimmte Konstante in der Lösung der DGL zu bestimmen. Formulieren Sie die vollständige DGL mit allen bekannten Zahlenwerten. |
||
#Stellen Sie diese DGL graphisch dar, z.B. in einem graphikfähigen Taschenrechner, in Wolfram Alpha, mit Microsoft Mathematics, mit Excel, Matlab oder einem anderen Tool Ihrer Wahl. Vergleichen Sie Ihr Resultat mit jenem von Berkeley-Madonna. |
#Stellen Sie diese DGL graphisch dar, z.B. in einem graphikfähigen Taschenrechner, in Wolfram Alpha, mit Microsoft Mathematics, mit Excel, Matlab oder einem anderen Tool Ihrer Wahl. Vergleichen Sie Ihr Resultat mit jenem von Berkeley-Madonna. |
||
'''[[Lösung zu DGL aus Berkeley Madonna|Lösung]]''' |
|||
Aktuelle Version vom 21. April 2015, 13:41 Uhr
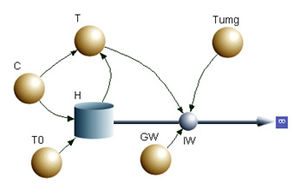
In der Vorlesung haben Sie das Berkeley-Madonna Modell zum Abkühlen einer Bierflasche kennengelernt. Die Abbildung zeigt das Flowchart dieses Modells. Die zugehörigen Gleichungen lauten
{Top model}
{Reservoirs}
- d/dt (H) = - IW
- INIT H = C*T0
{Flows}
- IW = GW * ( T - Tumg )
{Functions}
- C = 3770 {J/kg/K}
- T = H / C
- Tumg = 280 {K}
- GW = 8 {W/m/K}
T0 = 300 {K}
- Formulieren Sie aus den Gleichungen (Equations) des BM Modelles die zugehörige DGL.
- Lösen Sie die DGL mittels Wolfram Alpha oder eines CAS-fähigen Taschenrechners.
- Verwenden Sie die Anfangsbedingung, um die unbestimmte Konstante in der Lösung der DGL zu bestimmen. Formulieren Sie die vollständige DGL mit allen bekannten Zahlenwerten.
- Stellen Sie diese DGL graphisch dar, z.B. in einem graphikfähigen Taschenrechner, in Wolfram Alpha, mit Microsoft Mathematics, mit Excel, Matlab oder einem anderen Tool Ihrer Wahl. Vergleichen Sie Ihr Resultat mit jenem von Berkeley-Madonna.