U-Rohr

System

Ein offenes U-Rohr-Manometer beginnt zu schwingen, sobald man die eine Säule durch Anlegen eines Überdrucks hinunter presst und dann los lässt. Vergleicht man das Schwingungsverhalten eines mit Wasser gefüllten Manometers mit einem Quecksilbermanometer, stellt man in ihrem Schwingungsverhalten weder bezüglich Schwingungsdauer noch bezüglich Abklingverhalten einen grossen Unterschied fest. Beim Quecksilber muss man aber etwa dreizehn Mal stärker drücken als bei Wasser, um die gleich Auslenkung zu erhalten.

Modell

Systemdynamikmodell der U-Rohr-Schwingung

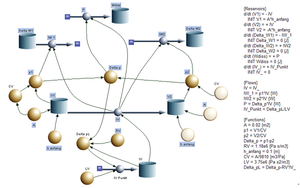
Das System U-Rohr kann in zwei Kapazitäten, einen Widerstand und eine Induktivität zerlegt werden. Die hydraulische Kapazität eines zylindrischen Gefässes ist gleich Querschnitt durch Dichte und Gravitationsfeldstärke. Widerstand und Induktivität können vom geraden Rohr übernommen werden. Messungen zeigen, dass diese Modellierung des Widerstandes zu grosse Abweichungen zwischen Modell- und Systemverhalten führt.

Das Volumen der beiden Kapazitäten darf bezüglich des Gleichgewichtszustandes angegeben werden. So bleibt das Gesamtvolumen der beiden Kapazitäten während des ganzen Vorganges gleich Null, d.h. der Druck in den beiden Kapazitäten schwingt um den Nullpunkt herum. Im vorliegenden Modell ist der Widerstand als reine Laminarströmung modelliert worden. Diese Annahme ist bequem und numerisch stabil, dürfte das Verhalten des realen Systems aber nicht all zu präzis beschreiben. Der Widerstandes in einem gekrümmten Rohr mit pulsierender Strömung ist sicher nicht einfach zu beschreiben sein.

Das Systemdiagramm zeigt die dynamische Struktur mit der Volumenbilanz, den beiden Rückkopplungsschleifen über kapazitives, resistives und induktives Gesetz sowie der Energiebetrachtung auf einer zweiten Bilanzebene. Die Energiebilanz umfasst die Änderung in den beiden Kapazitäten (Gravitationsenergie) sowie den Energieumsatz im Rohr (Bewegungsenergie und dissipierte Energie).

Simulation

IV, Δp_links sowie Δp_rechts

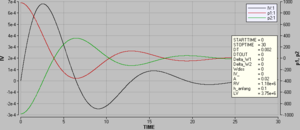
Verglichen mit dem Experiment klingt die Schwingung zu schnell ab. Das Dämpfungsverhalten der Wassersäule könnte mit Hilfe der Theorie der gedämpften Schwingung sicher besser abgeschätzt werden.

IV, Δp_links sowie Δp_rechts

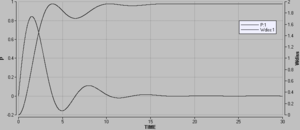
Das zweite Diagramm zeigt die hydraulische Prozessleistung über der Wassersäule sowie die vom Wasser aufgenommene Energie. Die Bezeichnung Diss für Dissipation ist nicht korrekt. Um die dissipierte Energie zu rechnen, dürfte man bei der Prozessleistung nur die Druckdifferenz über dem Widerstandselement einsetzen. Die hier formulierte Prozessleistung bezieht sich auf das resistive und das induktive Glied.