Fadenspule: Unterschied zwischen den Versionen
Inhalt hinzugefügt Inhalt gelöscht
Admin (Diskussion | Beiträge) KKeine Bearbeitungszusammenfassung |
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
[[Bild:Fadenspule. |
[[Bild:Fadenspule.png|thumb|Fadenspule]] |
||
Auf die nebenstehend skizzierte, ruhende Fadenspule ([[Masse]] 4 kg, [[Massenträgheitsmoment]] 0.1 kgm<sup>2</sup>, Abrollradius 30 cm, Wickelradius 20 cm) wirkt eine Kraft ein, die in vier Sekunden linear von Null auf 20 N anwächst. Die maximal mögliche Haftreibungskraft zwischen Spule und Unterlage beträgt 10 N. Sobald die Spule rutscht, nimmt die Gleitreibung auch den Wert von 10 N an. |
Auf die nebenstehend skizzierte, ruhende Fadenspule ([[Masse]] 4 kg, [[Massenträgheitsmoment]] 0.1 kgm<sup>2</sup>, Abrollradius 30 cm, Wickelradius 20 cm) wirkt eine Kraft ein, die in vier Sekunden linear von Null auf 20 N anwächst. Die maximal mögliche Haftreibungskraft zwischen Spule und Unterlage beträgt 10 N. Sobald die Spule rutscht, nimmt die Gleitreibung auch den Wert von 10 N an. |
||
#[[Freischneiden|Schneiden]] Sie die Fadenspule frei, d.h zeichnen Sie alle Kräfte ein, die auf die Spule wirken. |
#[[Freischneiden|Schneiden]] Sie die Fadenspule frei, d.h zeichnen Sie alle Kräfte ein, die auf die Spule wirken. |
||
Version vom 26. April 2007, 05:42 Uhr
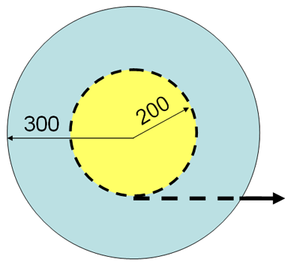
Auf die nebenstehend skizzierte, ruhende Fadenspule (Masse 4 kg, Massenträgheitsmoment 0.1 kgm2, Abrollradius 30 cm, Wickelradius 20 cm) wirkt eine Kraft ein, die in vier Sekunden linear von Null auf 20 N anwächst. Die maximal mögliche Haftreibungskraft zwischen Spule und Unterlage beträgt 10 N. Sobald die Spule rutscht, nimmt die Gleitreibung auch den Wert von 10 N an.
- Schneiden Sie die Fadenspule frei, d.h zeichnen Sie alle Kräfte ein, die auf die Spule wirken.
- Formulieren Sie die drei Bilanzgleichungen, die Grundgesetze der Mechanik.
- Welche zusätzliche Bedingung gilt in der Rollphase, welche in der Rutschphase?
- Wann beginnt die Spule zu gleiten?
- Wie schnell bewegt sich die Körperachse nach diesen vier Sekunden?
Quelle: Technikum Winterthur, Reformstudium Elektrotechnik 1996