Lösung zu Klotz auf schiefer Ebene

Aufgaben zur schiefen Ebene muss fast jeder Mittelschüler irgend einmal lösen. Doch wozu? Was lernt man dabei? Wenn man die fehlerhaften Lösungen in den gängigen Formelbüchern anschaut, kann man nur hoffen, dass dieses Paradepferd aus Ötzis Tagebuch bald aus den Schulstuben verschwinden wird.

1.

Kräfte und ihre Komponenten

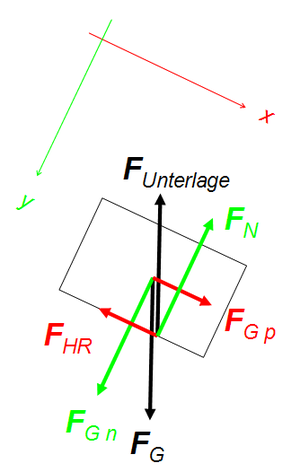
Auf den Klotz wirken nur die Gewichtskraft und die Unterlagskraft ein. Wählt man die z-Achse gegen unten, fliesst über das Gravitationsfeld z-Impuls in den Klotz hinein. Weil die Ebene den Klotz am Fallen hindert, muss dieser Impuls augenblicklich an die Unterlage weg strömen. Die Stärke des gravitativen Zuflusses nennt man Gewichtskraft, die Stärke des abfliessenden Impulsstromes heisst Unterlagskraft. Wählt man die x-Achse parallel und die y-Achse normal zur Ebene, können sowohl die Gewichts- als auch die Unterlagskraft in je zwei Komponenten zerlegt werden. Die Komponenten der Unterlagskraft heissen Normalkraft und Haftreibungskraft. Die eine Komponente der Gewichtskraft nennt man oft Hangabtrieb. Dass die andere Komponente der Gewichtskraft im deutschen Sprachraum ebenfalls Normkraft genannt wird, zeigt augenfällig, wie stümperhaft Mechanik an den Schulen unterrichtet wird. Wie kann man eine Komponente einer Oberflächenkraft mit der Komponente einer Volumenkraft verwechseln? Wer einmal begriffen hat, dass eine Kraft entweder die Stärke eines Impulsstromes bezüglich eines Körpers oder die Stärke der gravitativen Quelle im Körper beschreibt, kann sich ob so viel Unverstand nur wundern. Da sind die Ingenieure mit ihrem Schnittbild den Physiklehrern weit überlegen.

2. Jede Kraft lässt sich zu einer Wechselwirkung ergänzen, indem man den Partner einbezieht:

• Die Erde zieht den Klotz mit der Gewichtskraft nach unten. Folglich zieht der Klotz die Erde mit der entgegengesetzt gleichen Kraft nach oben.
• Die schiefe Ebene drückt mit der Unterlagskraft den Klotz nach oben und der Klotz drückt mit der entgegengesetzt gleichen Kraft die schiefer Ebene nach unten.

Das Wechselwirkungsprinzip enthält nur die triviale Aussage, wonach ein Impulsstrom von den beiden beteiligten Körpern aus gesehen die entgegengesetzt gleiche Stärke aufweist.

3. Die Haftreibungszahl beschreibt das Verhältnis von maximal möglicher Haftreibungskraft zur Normalkraft. Weil die Haftreibungskraft ihre Grenze erreicht hat, sobald der Klotz zu rutschen anfängt, kann die Haftreibungszahl aus der Analyse des Gleichgewichts im Grenzfall gewonnen werden

x-Richtung: [math]F_G \cos \varphi - F_{HRmax} = 0[/math]

y-Richtung: [math]F_N - F_G \sin \varphi = 0[/math]

Materialgesetz: [math]F_{HRmax} = \mu_H F_N[/math]

Die Lösung dieses Gleichungssystems liefert die Haftreibungszahl als Funktion des Grenzwinkels

[math]\mu_H = \tan \varphi[/math]

Für einen Grenzwinkel von 35° hat die Haftreibungszahl einen Wert von 0.7.

4. Weil sich der Körper danach in x-Richtung in Bewegung setzt, speichert er x-Impuls. Die Bilanzgleichungen für die beiden Impulskomponenten sowie das modifizierte Reibungsgesetz lauten dann

x-Richtung: [math]F_G \cos \varphi - F_{HRmax} = \dot p_x = m a[/math]

y-Richtung: [math]F_N - F_G \sin \varphi = = \dot p_y = 0[/math]

Materialgesetz: [math]F_R = \mu F_N[/math]

Dieses Gleichungssystem liefert für die Beschleunigung in x-Richtung einen Wert von

[math]a = g (\sin \varphi - \mu \cos \varphi)[/math] = 0.8 m/s².

5. Bewegt sich die Körper nach oben, wirkt die Gleitreibung nach unten. Deshalb muss das Vorzeichen vor der Gleitreibung geändert werden, was den Wert der Beschleunigung wesentlich verändert

[math]a = g (\sin \varphi + \mu \cos \varphi)[/math] = 10.5 m/s².

Was soll das?

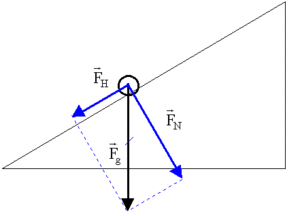
Als abschreckendes Beispiel sei hier noch eine Skizze aus dem Internet beigefügt:

• die Normalkomponente der Gewichtskraft wird hier als Normalkraft bezeichnet; mit dieser Bezeichnung kann in all den Beispielen, in denen die Normalkraft nicht gleich der Normalkomponente der Gewichtskraft ist (weil weitere Kräfte wirken oder die Unterlage gewölbt ist), das Gleitreibungsgesetz nicht mehr angewendet werden.
• die Unterlagskraft mit den beiden Komponenten Normalkraft und Haftreibungskraft fehlt; dabei ist gerade die Haftreibungskraft, die in diesem Fall nicht entgegengesetzt gleich gross wie die "Hangabtriebskraft" ist, für das Rollen auf der schiefen Ebene verantwortlich.

Aufgabe