Energiestrom und Prozessleistung

Der Begriff Energie ist vom schottischen Physiker William Rankine im Jahr 1852 eingeführt worden. Das Wort Energie leitet sich aus dem Griechischen ab (ἐν = in, innen und ἔργον = Werk, Wirken). Vor der Entdeckung des ersten Hauptsatzes der Wärmelehre, der die Energiebilanz bezüglich eines homogenen Systems beschreibt, kannte man die Energie nur in der Mechanik. Deshalb nannte man sie auch "lebendige Kraft" und sprach von der "Erhaltung der Kraft". 1905 hat Albert Einstein die Energie als eigenständige Grösse wieder abgeschafft, indem er zeigte, dass Energie und Masse äquivalent sind. Energie ist Masse, d.h. die Energie selber macht die Körper schwer und träge. Masse kann demnach auch nicht in Energie umgewandelt werden, weil Masse schon Energie ist.

Trotz der von Einstein gefundenen Gleichwertigkeit von Energie und Masse tun wir auch heute noch so, wie wenn die Energie eine eigenständige Grösse wäre. Dies ist auch ein Stück weit korrekt und sinnvoll. Nur sollte man sich immer bewusst sein, dass dem so verwendeten Energiebegriff enge Grenzen gesetzt sind.

Die Physik der dynamischen Systeme weist der Energie eine klare Rolle zu, die sich über alle Zweige der klassischen Physik erstreckt. Energie kann von einer zweiten Grösse transportiert und zusammen mit dieser gespeichert werden. Die pro Zeit mittransportierte Energie nennt man dann zugeordneter Energiestrom. Energie kann aber auch in einem Prozess von einem Energieträger auf einen andern umgeladen werden. Dabei setzt der erste Trägerstrom eine Prozessleistung frei und der zweite nimmt sie auf.

In dieser Vorlesung lernen Sie den zugeordneten Energiestrom und die Prozessleistung am Beispiel des Massen- und Volumenstromes kennen. Prägen Sie sich diese Grundstrukturen ein, denn diese tauchen immer wieder auf.

Lernziele

In dieser Vorlesung lernen Sie

• wie der zugeordnete Energiestrom in der Hydrodynamik berechnet wird
• von welchen Grössen die Leistung bei einem hydrodynamischen Prozess abhängt
• wann Energie Arbeitsvermögen und wann nur eine Bilanzgrösse ist
• wie man die transportierte Energie aus Volumenstrom und Druck berechnet
• wie man die umgesetzte Energie aus Volumenstrom und Druckdifferenz berechnet

Energiesysteme in einem Flugzeug

Energiesystem beim A380

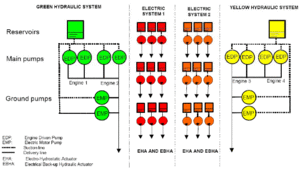
Gewöhnlich haben grosse Passagierflugzeuge drei unabhängig voneinander arbeitende hydraulische Systeme, mit denen Ruder und Klappen in den Flügeln bewegt werden. Diese Systeme arbeiten bisher mit einem Druck von 3000 psi (207 bar). Beim A 380 wurde der Druck in den Hydrauliksystemen auf 5000 psi (345 bar) erhöht. Dadurch können Leitungen mit einem um 30 % geringeren Durchmesser verwendet werden. Hätte man den Druck bei 3000 psi belassen, wären die Leitungen schnell armdick geworden. Jetzt liegt der maximale Durchmesser bei gut 2 Zoll (5,08 cm). Zudem wird es im Airbus A 380 nicht mehr drei, sondern nur noch zwei hydraulische Systeme geben. Das dritte System wird durch zwei elektrische ersetzt. Die Stellmotoren für Klappen und Ruder werden so entweder mit hydraulischer Energie fernversorgt oder eine elektrische Pumpe erzeugt den elektrischen Druck vor Ort am Stellantrieb.

Die Konstrukteure grosser Verkehrsflugzeuge können offensichtlich zwischen zwei Energietransportsystemen wählen, dem elektrischen und dem hydraulischen System. In beiden Fällen hängt der Energietransport von der Stromstärke und einer zweiten Grösse, die man Potenzial nennt, ab. Die Energiestromstärke (gemessen in Watt) hängt folglich von der elektrischen bzw. der Volumenstromstärke und dem elektrischen Potenzial bzw. dem Druck ab. Im internationalen Einheitensystem sind die Grössen so definiert, dass zur Berechnung des Energiestromes nur das Produkt aus Stromstärke (Energieträger)und Potenzial (Beladungsmass) gebildet muss.

Druck als Energiebeladungsmass

Eine unter Druck stehende Flüssigkeit wirkt allseits mit einer Kraft auf die Gefässwand ein. Schneidet man in Gedanken ein Stück aus der Gefässwand aus, ist diese Kraft gleich Fläche mal Druck. Nun ist, wie Sie vielleicht schon gehört haben, eine Kraft eine Impulsstromstärke bezüglich eines Körpers. Der Druck darf deshalb als Impulsstromstärke pro Querschnittfläche bezeichnet werden. Der Druck ist also eine Impulsstromdichte. Leider ist der Sachverhalt etwas komplexer. In ruhenden Flüssigkeiten und Gasen beschreibt der Druck eine dreifache Impulsstromdichte. In diesen Medien fliesst jede der drei Impulskomponenten mit gleicher Stärke in die eigene Bezugsrichtung. In bewegten Fluiden und festen Körpern können dagegen alle drei Komponente des Impulses in alle drei Richtungen transportiert werden. Folglich benötigt man neun Zahlen (drei Mengen und drei Raumrichtungen), um den Impulstransport an einem bestimmten Punkt eines Körpers zu beschreiben. Die Fachleute bezeichnen die (negative) Impulsstromdichte auch als Spannungstensor. Mehr dazu im Teil Translationsmechanik.

In der Hydro- und Thermodynamik erscheint der Druck als Potenzial. Der Druck ist das Energiebeladungsmass der Volumenstromes: je höher der Druck in einer Flüssigkeit oder einem Gas, desto mehr Energie wird vom Fluidum mitgenommen. Diese Bedeutung des Drucks ist viel einfacher zu verstehen als der Zusammenhang mit Kraft und Impuls. Als betrachten wir den Druck vorerst nur als Energiebeladungsmass oder hydrodynamisches Potenzil.

In hydraulischen Systemen wird Energie transportiert. Der vom Öl transportierte Energiestrom ist um so grösser, je höher der Druck ist und je mehr Öl durch die Leitung fliesst. Der Zusammenhang zwischen der Volumenstromstärke I_V, dem Druck und dem zugeordnetem Energiestrom ist denkbar einfach: der zugeordnete Energiestrom I_W ist gleich Druck mal Volumenstromstärke

[math]I_W = p I_V[/math]

Der Energiestrom wird in Watt (W) gemessen und der Volumenstrom in Kubikmeter pro Sekunde. Folglich muss der Druck in Wattsekunde pro Kubikmeter oder Joule pro Kubikmeter angegeben werden. Für diese Druckeinheit existiert ein eigener Name: Pascal (Pa). Ein Pascal ist ein Joule pro Kubikmeter. Mit Hilfe des internationalen Einheitensystems kann Pascal auf die Basiseinheiten zurückgeführt werden

1 Pa = 1 kg/(s²m) )= 1 Ws/m³ = 1 J/m²

Verteilt man eine Tafel (100 g) Schokolade gleichmässig über einen Tisch mit einem Quadratmerter Tischfläche, ist der Druck an der Unterseite der Schokoladeschicht um ein Pascal grösser als auf der Oberseite. Pascal ist eine sehr kleine Einheit. Deshalb ist mit Bar auch noch eine zweite Druckeinheit zugelassen. Ein Bar sind hunderttausend Pascal

1 bar = 10⁵ Pa

Misst man den Druck in Bar statt in Pascal, muss der Volumenstrom in Zentiliter pro Sekunde messen, damit für den Energiestrom wieder Watt heruaskommt

1 W = 1 bar * 1 cl/s

zugeordneter Energiestrom

Die in einem hydraulischen System transportiere Energie ist gleich Druck mal Volumenstromstärke

[math]I_W = p I_V[/math]

Druck und Volumenstrom in der Arterie

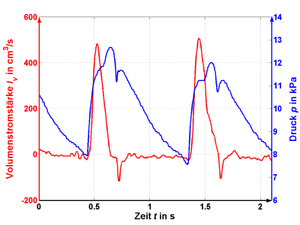
Das Bild zeigt Druck und Volumenstrom in der Arterie eines Menschen in Funktion der Zeit. Bei einem Herzschlag steigt der Druck in kurzer Zeit an und es fliesst viel Blut durch die Aorta. Der Volumenstrom fällt dann rasch ab und der Druck steigt noch etwas höher. Danach kommt es zum interessanten Phänomen der Blutrückflusses. Anhand dieses Diagramms kann man nun mehrere Fragen beantworten

• Wann transportiert der Blutstrom am meisten hydraulische Energie?
• Wie gross ist dann die Fliessgeschwindigkeit?
• Wie wird die Energie beim Rückfluss des Blutes transportiert?
• Wie viel Energie wird während eines Herschlags durch die Aorta transportiert?

Das Produkt aus Druck und Volumenstrom ergibt den zugeordneten Energiestrom. Solange beide Grössen in der Zeit zunehmen, wächst die Stromstärke der mittransportierten Energie an. Weil im Bereich der Stromspitze der Druck nur noch leicht zunimmt, liegt das Maximum der Energiestromstärke ein klein wenig rechts des maximalen Volumenstromes. Der Strom erreicht einen Spitzenwert von 480 cm³/s bei einem Druck von 11.7 kPa. Rechnet man den Volumenstrom in Kubikmeter pro Sekunde und den Druck in Pascal um, ergibt das Produkt der beiden Grössen einen zugeordneten Energiestrom von 5.6 Watt. 60 Mal die Sekunde während etwa 80 Jahren muss das Herz diese Spitzenleistung erbringen (Sport, Stress und Sex noch nicht mitgerechnet).

Die Fliessgeschwindigkeit ist gleich Volumenstromstärke durch Querschnittfläche (vergl.: Bilanzieren). Bei einem Querschnitt von 6 cm² ergibt dies eine Geschwindigkeit von 80 cm/s oder 0.8 m/s. Dieser Wert sollte nicht mit der Pulsgeschwindigkeit, die bei einem gesunden Menschen etwa 4 - 9 m/s beträgt, verwechselt werden.

Kurzfristig strömt das Blut in der Aorta gegen das Herz. Nimmt man die Spitze von 110 cm³/s und multipliziert diesen Wert mit dem Druck, der dann immer noch 11.7 kPa beträgt, erhält man einen zugeordneten Energiestrom von 1.3 W, der mit dem Blut und damit gegen das Herz fliesst. Die Energie wird mit dem Volumen transportiert, solange der Druck positiv ist. Weil wir hier mit dem Überdruck gegen die Umgebung rechnen, könnte der Druck negativ werden. Das passiert beim Einatmen. Dann fliesst die Luft durch die Luftröhre und Bronchien in die Lunge hinein, der zugeordnete Energiestrom fliesst dann infolge des negativen Drucks (Unterdruck) in die entgegengesetzte Richtung, also gegen Mund und Nase. Dies entspricht auch unserer Empfindung. Die Lunge erzeugt einen Sog, der die Luft aktiv hinein zieht. Nimmt man statt des Über- oder Unterdrucks den Absolutdruck, der immer positiv ist, fliesst die Energie ohne Einschränkung mit dem Volumenstrom. Zudem würden alle Werte des zugeordneten Energiestromes um ein Bar mal die Volumenstromstärke grösser.

Merken wir uns zwei Dinge

1. Die zugeordnete Energiestrom ist eine reine Bilanzgrösse. Sein Wert, die Energiestromstärke gemessen in Watt, hängt von der Wahl des Bezugspunktes des Drucks ab (Nullpunkt des Potentials).
2. Solange der Druck positiv ist, fliesst die Energie mit dem Volumenstrom. Nimmt der Druck negative Werte an, fliessen Volumen und Energie gegeneinander.

transportierte Energie

transportierte Energie

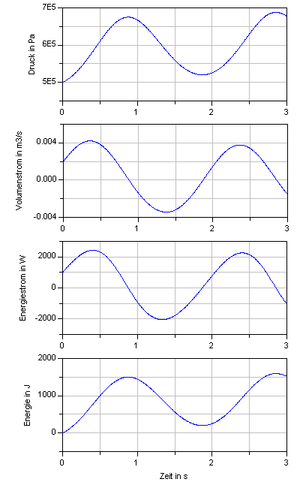
Solange Druck und Volumenstrom konstant bleiben, ist die Frage nach der transportierten Energie einfach zu beantworten. Man berechnet zuerst den zugeordneten Energiestrom (Druck mal Volumenstrom) und multipliziert diesen Wert danach mit der Zeit. Steigen Druck und Volumenstrom linear an, könnte man die Werte nach dem halben Zeitabschnitt (Mittelwerte) nehmen, das Produkt bilden und mit dem Zeitabschnitt multiplizieren. Dieses Verfahren liefert aber den falschen Wert. Nachfolgend werden nun zwei Berechnungsverfahren vorgestellt. Mindestens eines der beiden sollten Sie beherrschen. Im Modellbildungslabor werden Sie dann noch lernen, wie man die transportierte Energie mit Hilfe eines systemdynamischen Werkzeuges ermittelt.

Beim ersten Verfahren bestimmt man den zugeordneten Energiestrom zu verschiedenen Zeitpunkten (möglichst viele) und überträgt diese Werte in ein Energiestrom-Zeit-Diagramm. Danach wendet man das gleiche Verfahren wie beim Volumgenstrom an: die transportierte Energie ist gleich der Fläche unter dem Energiestrom-Zeit-Diagramm (vergl.:Bilanzieren). Nimmt der Energiestrom negative Werte an, weil das Volumen zurück fliesst oder der Druck negativ wird, müssen die entsprechenden Flächenabschnitte negativ gezählt werden.

Das zweite Verfahren, das auf die Idee eines Studierenden am TWI zurückgeht, basiert auf einem dreidimensionalen Schaubild. Man fügt das Volumenstrom-Zeit- und das Druck-Zeit-Diagramm längs der Zeitachse so zusammen, dass sich die Volumenstrom und die Druckachse in einem rechten Winkel schneiden. Schaut man von vorn auf dieses 3D-Schaubild, bilden Volumenstrom- und Druckachse zusammen mit dem momentanen Wert ein Rechtecke, dessen Fläche dem zugeordneten Energiestrom entspricht. Die Summe über all diese Rechtecke bildet dann einen Körper, der den Wert der transportierten Energie repräsentiert. Aus diesem Schaubild können neben den Werten von Druck und Volumenstrom der zugeordnete Energiestrom (Fläche des Rechtecks), das transportiert Volumen (Fläche unter der Volumenstrom-Zeit-Kurve) und die transportierte Energie (Volumen eines Körpers) herausgelesen werden.

Der Zusammenhang zwischen Druck, Volumenstrom und zugeordneten Energiestrom kann mittels eines Java-Applets dynamisch dargestellt werden. Lassen Sie das Applet einmal laufen, geben Sie eigene Werte ein und versuchen Sie, alle Zusammenhänge zu begreifen.

Prozessleistung

Im Gravitationsfeld der Erde schreibt man jedem Körper eine Gravitationsenergie (potentielle Energie) zu. Diese Energie ist gleich dem Produkt aus Masse und Gravitationspotenzial. Demnach wird das Gravitationspotenzial in Joule pro Kilogramm gemessen. Das Gravitationspotenzial mimmt in der Nähe der Erdoberfläche pro Meter Höhe um zehn Joule pro Kilogramm zu. Setz man das Gravitationspotenzial auf Meereshöhe gleich Null, weist der Titicaca-See an der Oberfläche (3800 m.ü.M.) ein Gravitationspotenzial von 38 kJ/kg, der Zürichsee (400 m.ü.M.) 4 kJ/kg und das Tote Meer (400 m.u.M.) -4 kJ/kg auf. Folglich kann jedem Liter Wasser, der in der Limmat durch Zürich fliesst, eine potenzielle Energie von 4 kJ zugeschrieben werden. Führt die Limmat 100 m³ oder 100 t Wasser pro Sekunde, transportiert sie einen zugeordneten Energiestrom von 400 MJ/s oder 400 MW. Mit diesem Strom könnte man einen beachtlichen Teil der Stadt mit Energie versorgen.

Wasser, das von Zürich bis nach Holland fliesst, setzt pro Kilogramm eine Energie von 4 kJ frei. Die Energie wird aber nur an den Stellen freigesetzt, an denen ein Gefälle vorhanden ist. Und damit kommen wir zu einem wesentlichen Punkt im Umgang mit der Energie:

• jedem Massenstrom wird ein Energiestrom zugeordnet: [math]I_W = \varphi_G I_m[/math]
• fällt der Massenstrom über eine Stufe hinunter, wird eine Prozessleistung freigesetzt: [math]P = I_{W1} - I_{W2} = \Delta \varphi I_m[/math]

Mathematisch kann die Prozessleistung aus dem zugeordneten Energiestrom durch Vergleich an zwei Punkten abgeleitet werden. Dennoch besteht zwischen diesen beiden Grössen ein grosser Unterschied

• zugeordneter Energiestrom:
  • reine Bilanzgrösse
  • Wert hängt vom Bezugspunkt des Potenzials ab
• Prozessleistung:
  • Arbeitsvermögen pro Zeit
  • Wert hängt von keinem Bezug ab

Geht man vom Massenstrom zum Volumenstrom über, muss das Gravitationspotenzial durch den Druck ersetzt werden. Am Unterschied zwischen zugeordnetem Energiestrom und Prozessleistung ändert sich aber nichts

• jedem Volumenstrom wird ein Energiestrom zugeordnet: [math]I_W = p I_V[/math]
• fällt der Volumenstrom über ein Druckgefälle, wird eine Prozessleistung freigesetzt: [math]P = I_{W1} - I_{W2} = \Delta p I_V[/math]

Materialien

Zurück zum Inhalt