Ladungs- und Energiespeicher: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) |
||
| Zeile 23: | Zeile 23: | ||
wobei mit ''r<sub>1</sub>'' der Aussenradius der Innenkugel und mit ''r<sub>2</sub>'' der Innenradius der Aussenkugel gemeint ist. Auf der Innenkugel sitzt die Ladung auf der Aussenfläche und auf der Aussenkugel auf der Innenfläche, weil sich das elektrische Feld nur über den Zwischenraum erstreckt (ein elektrisches Feld in den Metallteilen würde gemäss dem Ohmschen Gesetz einen Strom antreiben). |
wobei mit ''r<sub>1</sub>'' der Aussenradius der Innenkugel und mit ''r<sub>2</sub>'' der Innenradius der Aussenkugel gemeint ist. Auf der Innenkugel sitzt die Ladung auf der Aussenfläche und auf der Aussenkugel auf der Innenfläche, weil sich das elektrische Feld nur über den Zwischenraum erstreckt (ein elektrisches Feld in den Metallteilen würde gemäss dem Ohmschen Gesetz einen Strom antreiben). |
||
Je kleiner der Spalt zwischen den beiden Kugeln (''r<sub>2</sub> - r<sub>1</sub>''), desto kürzer das Feld, desto kleiner die Spannung bei gegebener Ladung und um so grösser die Kapazität. Wählt man den Spalt immer enger, darf die Spannung zwischen den beiden Kugeln nicht zu gross werden, weil die Elektronen durch das starke Feld heraus gerissen werden können und so einen Kurzschlussstrom bilden, der die Ladung ausgleichen. Um diesen Kurzschluss zu verhindern, füllt man den Zwischenraum mit einem Material, dem [[Dielektrikum]], aus. Mit dem Dielektrikum erhöht man nicht nur die maximal möglich Spannung, sondern schwächt auch noch das durch die Ladung erzeugte Feld ab. |
Je kleiner der Spalt zwischen den beiden Kugeln (''r<sub>2</sub> - r<sub>1</sub>''), desto kürzer das Feld, desto kleiner die Spannung bei gegebener Ladung und um so grösser die Kapazität. Wählt man den Spalt immer enger, darf die Spannung zwischen den beiden Kugeln nicht zu gross werden, weil die Elektronen durch das starke Feld heraus gerissen werden können und so einen Kurzschlussstrom bilden, der die Ladung ausgleichen. Um diesen Kurzschluss zu verhindern, füllt man den Zwischenraum mit einem Material, dem [[Dielektrikum]], aus. Mit dem Dielektrikum erhöht man nicht nur die maximal möglich Spannung, sondern schwächt auch noch das durch die Ladung erzeugte Feld ab. Den Einfluss des durch das Dielektrikum verursachte Schwächung des elektrischen Feldes wird mit der Dielektrizitätszahl beschrieben. Das Produkt aus '''elektrischer Feldkonstante''' (''ε<sub>0</sub>'') und '''Dielektrizitätszahl''' (''ε<sub>r</sub>'') nennt '''Dielektrizitätskonstante''' (''ε'') |
||
:<math>\varepsilon=\varepsilon_r\varepsilon_0</math> |
|||
Diese Konstruktion mag etwas kompliziert tönen, hat aber den Vorteil, dass die [[Kapazität]]en der [[Kondensator]]en im Vakuum berechnet und können. Ist der Zwischenraum mit einem Dielektrikum gefüllt, schreibt man überall statt ''ε<sub>0</sub>'' nur ''ε''. |
|||
==hydroelektrische Analogie== |
==hydroelektrische Analogie== |
||
Version vom 27. September 2007, 07:46 Uhr
Elektrische Ladung kann kaum gespeichert werden, weil das von dieser Ladung erzeugte Feld extrem stark ist. Würde man die Natrium- und Chlor-Ionen von nur einem Gramm Kochsalz trennen und auf den Nordpol bzw. dem Südpol der Erde bringen, würden sich diese beiden Teile des Kochsalzes mit 150 N anziehen.
Ladung kann nur gespeichert werden, wenn das zugehörige Feld möglichst klein und möglichst schwach gehalten wird. Deshalb sind elektrische Kondensatoren so gebaut, dass das von der Ladung erzeugte Feld möglich geschwächt und in seiner räumlichen Ausdehnung weitgehend begrenzt wird.
Kapazität einer Kugel
In den einführenden Experimenten haben wir isolierte Metallkugeln mit einem geriebenen Glasstab geladen oder mit einem geriebenen Bernstein entladen. Die mit den Kugeln verbundenen Elektrometer zeigten dann das zugehörige Potenzial, die Spannung gegen Erde, an. Nun kann man auf eine grosse Kugel mehr Ladung bringen als auf eine kleine, weil die grosse Kugel über mehr Kapazität als die kleine verfügt. In der Elektrodynamik wird die Kapazität analog zur Hydrodynamik definiert. Die Kapazität ist gleich dem Verhältnis von gespeicherter Ladung zu der dadurch verursachten Spannung
- [math]C=\frac{Q}{U}[/math]
Im falle der Metallkugel (es könnte auch ein anders geformter Körper sein) ist die Spannung immer gegen Erde zu nehmen. Weil die umgebenden Körper das zugehörige elektrische Feld beeinflussen, wirken sich diese auch auf das Potenzial der Kugel aus. Befindet sich die Metallkugel (Radius r) weit weg von allen andern Leitern, kann für deren Kapazität eine einfache Formel angegeben werden
- [math]C=4\pi\varepsilon_0 r[/math]
Epsilon ist die elektrische Feldkonstante (ε0 = 8.854 10-12 F/m). Interessanterweise nimmt die Kapazität einer Kugel nicht proportional zum Volumen oder zur Oberfläche sondern linear mit dem Radius zu. Um dies zu zeigen, muss man mehr von elektrischen Feldern verstehen.
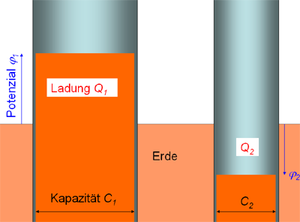
Der Zusammenhang zwischen Ladung, Kapazität und Potenzial lassen sich sehr schön im Flüssigkeitsbild darstellen. Stellt man sich die Ladung als Flüssigkeit, die Körper als zylindrische Gefäss und die Kapazität als Querschnitt dieser Gefässe vor, verwandelt sich das Potenzial in eine Füllhöhe. Die Ladung kann dann als Kapazität mal Potenzial (Grundfläche mal Höhe) geschrieben werden.
Kondensatoren
Umhüllt man eine elektrisch geladene Metallkugel mit einer zweiten, die geerdet ist, fliess von der zweiten Kugel gleich viel Ladung weg, wie auf der ersten gespeichert ist. Dieses Phänomen, Influenz genannt, führt dazu, dass ausserhalb der beiden Kugeln kein elektrisches Feld mehr nachzuweisen ist. So erreicht man zwei Dinge: erstens stört das eingeschlossene Feld keine andern Systeme im Aussenraum und zweitens wird das elektrische Feld räumlich begrenzt, was die Kapazität beträchtlich erhöht. Die Kapazität eines Kugelkondensators (zwei konzentrische Kugeln mit je einem Anschluss) ist gleich
- [math]C=4\pi\varepsilon_0\frac{r_2r_1}{r_2-r_1}[/math]
wobei mit r1 der Aussenradius der Innenkugel und mit r2 der Innenradius der Aussenkugel gemeint ist. Auf der Innenkugel sitzt die Ladung auf der Aussenfläche und auf der Aussenkugel auf der Innenfläche, weil sich das elektrische Feld nur über den Zwischenraum erstreckt (ein elektrisches Feld in den Metallteilen würde gemäss dem Ohmschen Gesetz einen Strom antreiben).
Je kleiner der Spalt zwischen den beiden Kugeln (r2 - r1), desto kürzer das Feld, desto kleiner die Spannung bei gegebener Ladung und um so grösser die Kapazität. Wählt man den Spalt immer enger, darf die Spannung zwischen den beiden Kugeln nicht zu gross werden, weil die Elektronen durch das starke Feld heraus gerissen werden können und so einen Kurzschlussstrom bilden, der die Ladung ausgleichen. Um diesen Kurzschluss zu verhindern, füllt man den Zwischenraum mit einem Material, dem Dielektrikum, aus. Mit dem Dielektrikum erhöht man nicht nur die maximal möglich Spannung, sondern schwächt auch noch das durch die Ladung erzeugte Feld ab. Den Einfluss des durch das Dielektrikum verursachte Schwächung des elektrischen Feldes wird mit der Dielektrizitätszahl beschrieben. Das Produkt aus elektrischer Feldkonstante (ε0) und Dielektrizitätszahl (εr) nennt Dielektrizitätskonstante (ε)
- [math]\varepsilon=\varepsilon_r\varepsilon_0[/math]
Diese Konstruktion mag etwas kompliziert tönen, hat aber den Vorteil, dass die Kapazitäten der Kondensatoren im Vakuum berechnet und können. Ist der Zwischenraum mit einem Dielektrikum gefüllt, schreibt man überall statt ε0 nur ε.