Impulsstrombild

Impuls kann leitungsartig, feldartig oder konvektiv durch den Raum transportiert werden. Im Falle des leitungsartigen Transportes entspricht die Impulsstromdichte (Impuls pro Zeit und Querschnittfläche) bis auf das Vorzeichen dem Spannungstensor. Zerlegt man den Spannungstensor mit Hilfe eines Koordinatensystems in seine neun Komponenten, erhält man eine symmetrische Matrix mit drei Zeilen und drei Spalten. Nun beschreibt jede dieser Spalten die Stromdichte einer der drei Impulskomponenten. Ordnet man jeder Spalte einen eigenen Vektor zu, erhält man insgesamt drei Bilder, welche den Transport von je einer Impulskomponente darstellen. Aus diesen drei Impulsstrombildern geht hervor, wie der Impuls durch ein Bauteil fliesst. Nachfolgend ein paar Beispiele

Blechstück unter Zug

x- und y-Impulsstrom in einem Stück Blech

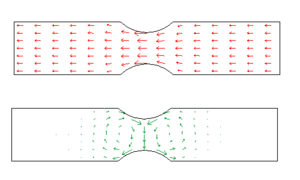
Das erste Bild zeigt den Impulsstrom durch einen beidseits eingekerbten Blechstreifen. Im Bereich der Kerben wird der primäre Impulsstrom gegen die Mitte hin abgelenkt. Dabei entstehen Wirbelströme der zweiten Impulskomponente. Schuld an dieser Wirbelbildung ist das Prinzip der zugeordneten Schubspannung (Symmetrie des Spannungstensors). In der Sprache der Impulsströme besagt dieses Prinzip, dass ein y-Impulsstrom in x-Richtung fließen muss, sobald der x-Impulsstrom in die y-Richtung ausweicht. Allgemein formuliert muss die j-Komponente der i-Impulsstromdichte an jedem Ort gleich der i-Komponente der j-Impulsstromdichte sein (i und j stehen für x, y und z).

Im naiven Bild des Kraftflusses nimmt man an, dass das eingekerbte Blech an der schwächsten Stelle reist, weil dort die Kraft auf einen engeren Querschnitt konzentriert ist. Doch weil der gegen die Mitte abgelenkte Primärfluss (hier rot dargestellt) zusätzlich noch Wirbel der konjugierten Komponente verursacht, wächst in der Umgebung der Kerbe die Belastung des Material stärker an, das naive Bild des Kraftflusses vermuten lässt.