Impulsstrombild
Impuls kann leitungsartig, feldartig oder konvektiv durch den Raum transportiert werden. Im Falle des leitungsartigen Transportes entspricht die Impulsstromdichte (Impuls pro Zeit und Querschnittfläche) bis auf das Vorzeichen dem Spannungstensor. Zerlegt man den Spannungstensor mit Hilfe eines Koordinatensystems in seine neun Komponenten, erhält man eine symmetrische Matrix mit drei Zeilen und drei Spalten. Nun beschreibt jede dieser Spalten die Stromdichte einer der drei Impulskomponenten. Ordnet man jeder Spalte einen eigenen Vektor zu, erhält man insgesamt drei Bilder, welche den Transport von je einer Impulskomponente darstellen. Aus diesen drei Impulsstrombildern geht hervor, wie der Impuls durch ein Bauteil fliesst. Nachfolgend ein paar Beispiele
Blechstück unter Zug
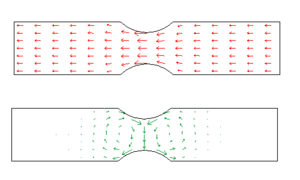
Das erste Bild zeigt den Impulsstrom durch einen beidseits eingekerbten Blechstreifen. Im Bereich der Kerben wird der primäre Impulsstrom gegen die Mitte hin abgelenkt. Dabei entstehen Wirbelströme der zweiten Impulskomponente. Schuld an dieser Wirbelbildung ist das Prinzip der zugeordneten Schubspannung (Symmetrie des Spannungstensors). In der Sprache der Impulsströme besagt dieses Prinzip, dass ein y-Impulsstrom in x-Richtung fließen muss, sobald der x-Impulsstrom in die y-Richtung ausweicht. Allgemein formuliert muss die j-Komponente der i-Impulsstromdichte an jedem Ort gleich der i-Komponente der j-Impulsstromdichte sein (i und j stehen für x, y und z).
Im naiven Bild des Kraftflusses nimmt man an, dass das eingekerbte Blech an der schwächsten Stelle reist, weil dort die Kraft auf einen engeren Querschnitt konzentriert ist. Doch weil der gegen die Mitte abgelenkte Primärfluss (hier rot dargestellt) zusätzlich noch Wirbel der konjugierten Komponente verursacht, wächst in der Umgebung der Kerbe die Belastung des Material stärker an, das naive Bild des Kraftflusses vermuten lässt.
Die Impulsstromdichte, die Spannung, erzeugt die Deformation. Bei homogenen Stoffen kann der Zusammenhang zwischen Impulsstromdichte (Spannungstensor) und Dehnung (Dehnungstensor) mit nur zwei Materialgrössen (z.B. Kompressionsmodul und Schubmodul) beschrieben werden. Die exakte Gestalt der Impulsstrombilder, die Spannungsverteilung über das ganze Bauteil, ist das Ergebnis aus dem Zusammenspiel von Spannung (Impulsstromdichte) und Geometrie (Dehnung).
Bügel
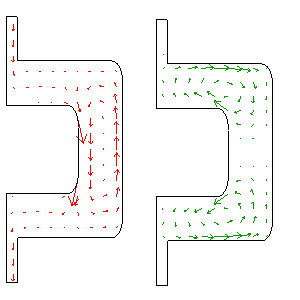
Ein Bügel steht unter Zug, d.h. der Bügel wird von einem primären Impulsstrom (rot, nachfolgend x-Komponente genannt) durchflossen. Zug bedeutet, dass die entsprechende Impulskomponente gegen die eigene Bezugsrichtung transportiert wird. Der Bügel zwingt den x-Impulsstrom zu einem Umweg in y-Richtung (nach rechts). Dadurch bildet sich in beiden Armen des Bügels je ein Impulswirbel (grün, nachfolgend y-Komponente genannt). Im zentralen Teil des Bügels entsteht sogar ein Tertiärwirbel. Das Bild mit den roten Pfeilen zeigt dort die Überlagerung aus Primär- und Tertiärstrom.
Die Impulsstrombilder zeigen die Stärke und die Art der Belastung
- Entlang der äusseren Begrenzung des Bügels fliessen sowohl die x- (rot) als auch die y-Ströme (grün) in die eigene Bezugsrichtung; folglich ist dort das Material auf Druck belastet.
- Im inneren Teil des Bügels fliessen beide Impulskomponenten gegen die eigene Bezugsrichtung; diese Impulsströme belasten das Material auf Zug.
Weil die Wirbelströme bedeutend stärker als der primäre Strom sind, muss jeder Bügel, der zwischen zwei Seile gespannt wird, stark genug gebaut werden.
Auf einer zweiten Beschreibungsebene kann der Transport von Drehimpuls diskutiert werden:
- im oberen Arm des Bügels bildet der in y-Richtung fliessende x-Impulsstrom eine z-Drehimpulsquelle (Hebelgesetz)
- im unteren Arm erzeugt der gleiche Strom eine entgegen gesetzt gleich starke Senke.
- der von der Quelle zur Senke fliessende Drehimpulsstrom wird von zusätzlichen Impulsströmen begleitet (Sekundär- und Tertiärwirbel)
In der Statik nennt man die Stärke des Drehimpulsstromes je nach Transportrichtung Biegemoment (quer zur Bezugsrichtung) oder Torsionsmoment (parallel zur Bezugsrichtung). Zeichnet man die Stärke des in einem Balken querfliessenden Drehimpulsstromes auf, sprechen die Fachleute von Biegemomentenverlauf.