Lösung zu Steigflug: Unterschied zwischen den Versionen
Inhalt hinzugefügt Inhalt gelöscht
(Detaillieren) |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
Das Flugzeug kann nur mit dem Gravitationsfeld und der umgebenden Luft [[Impuls]] austauschen. Die [[Impulsstrom]]stärke bezüglich der gesamten Flugzeugoberfläche kann in einen statischen sowie einen dynamischen Auftrieb, einen Luftwiderstand und eine Schubkraft zerlegt werden. Den statischen Auftrieb berücksichtigt man meistens nicht (mit einer Waage misst man immer die Differenz von Gewichtskraft und statischem Auftrieb in Luft). |
Das Flugzeug kann nur mit dem Gravitationsfeld und der umgebenden Luft [[Impuls]] austauschen. Die [[Impulsstrom]]stärke bezüglich der gesamten Flugzeugoberfläche kann in einen statischen sowie einen dynamischen Auftrieb, einen Luftwiderstand und eine Schubkraft zerlegt werden. Den statischen Auftrieb berücksichtigt man meistens nicht (mit einer Waage misst man immer die Differenz von Gewichtskraft und statischem Auftrieb in Luft). |
||
[[Bild:Kraefte Steigflug.jpg|thumb|Kräfte-Diagramm]] |
|||
Steigwinkel <math>\beta = arctan(\frac {10 m/s} {90 m/s}) = 6.34^\circ</math> |
Steigwinkel <math>\beta = arctan(\frac {10 m/s} {90 m/s}) = 6.34^\circ</math> |
||
Version vom 27. Dezember 2007, 12:28 Uhr
Das Flugzeug kann nur mit dem Gravitationsfeld und der umgebenden Luft Impuls austauschen. Die Impulsstromstärke bezüglich der gesamten Flugzeugoberfläche kann in einen statischen sowie einen dynamischen Auftrieb, einen Luftwiderstand und eine Schubkraft zerlegt werden. Den statischen Auftrieb berücksichtigt man meistens nicht (mit einer Waage misst man immer die Differenz von Gewichtskraft und statischem Auftrieb in Luft).
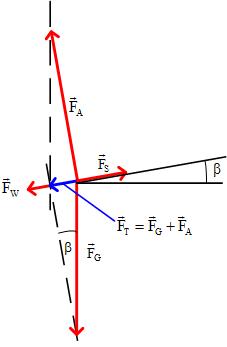
Steigwinkel [math]\beta = arctan(\frac {10 m/s} {90 m/s}) = 6.34^\circ[/math]
- Gewichtskraft, Luftwiderstand, dynamischer Auftrieb und Schub halten hier das Flugzeug im Gleichgewicht. Folglich muss der dynamische Auftrieb gleich der normal zur Anströmung stehenden Komponente der Gewichtskraft, also kleiner als die Gewichtskraft, sein.
- Der Auftrieb ist gleich [math]F_A= F_G \cdot \cos (\beta) = m g \cos (\beta)[/math] = 117 kN.
- In Flugrichtung wirken die Tangentialkomponente des Gewichts, der Luftwiderstand und die Schubkraft. Folglich ist der Luftwiderstand gleich [math]F_W= \frac {F_G}{4} - \frac {10}{90} F_G = \frac {5}{36} m g[/math] = 16.35 kN.
- Aus der Formel für den dynamischen Auftrieb folgt [math]A = \frac {2 F_A}{\rho c_A v^2}[/math] = 23.9 m2.
- Auftriebsbeiwert und Widerstandsbeiwert stehen im gleichen Verhältnis wie Auftriebskraft zu Widerstandskraft, falls sich die Beiwerte - wie hier angenommen - auf die gleiche wirksame Fläche beziehen. Also ist der Widerstandsbeiwert gleich 0.154.