Fussball: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) |
||
| Zeile 36: | Zeile 36: | ||
Die Zahl ''c<sub>M</sub>'' heisst Mangusbeiwert und hängt von der Beschaffenheit des Balls sowie von der Anströmgeschwindigkeit ab. |
Die Zahl ''c<sub>M</sub>'' heisst Mangusbeiwert und hängt von der Beschaffenheit des Balls sowie von der Anströmgeschwindigkeit ab. |
||
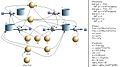
Das erste Bild zeigt das Systemdiagramm (flowchart) zur Berechnung des Abstosses. Im Gegensatz zur Magnusrolle ist hier die Abnahme der Winkelgeschwindigkeit infolge der Luftreibung nicht modelliert. Im zweiten Bild ist die Bahn des Balls mit einer Winkelgeschwindigkeit von 60 s<sup>-1</sup> (etwa 10 Umdrehungen pro Sekunde)und verschiedenen Abschusswinkeln dargestellt. Das dritte Bild zeigt die Bahnen bei einem Abschusswinkel von 25° und verschiedenen Winkelgeschwindigkeiten. |
|||
<gallery> |
<gallery> |
||
Bild:Fussball 2SD.jpg|Systemdiagramm (flowchart) |
Bild:Fussball 2SD.jpg|Systemdiagramm (flowchart) |
||
Version vom 4. Juni 2008, 06:27 Uhr
Fußssball ist eine Sportart, bei der zwei Mannschaften mit je elf Spielern (einem Torhüter und zehn Feldspielern) gegeneinander antreten. Ziel des Spiels ist es, den Ball möglichst oft ins gegnerische Tor zu bringen. Nach den Regeln des DFB ist ein Fussball regelgerecht, wenn er
- kugelförmig ist,
- aus Leder oder einem anderen geeigneten Material gefertigt ist,
- einen Umfang zwischen mindestens 68 und höchstens 70 cm hat,
- zu Spielbeginn mindestens 410 und höchstens 450 Gramm wiegt und
- sein Überdruck 0.6–1.1 Atmosphären beträgt.
Unser Modellball habe eine Masse von 0.44 kg und einen Durchmesser von 22 cm (Querschnitt 3.8 dm2).
Abstoss
Der Abstoss wird meist von einem Torwart ausgeführt, in seltenen Fällen auch von einem Spieler. Beim Abstoss darf sich kein weiterer Spieler im Strafraum aufhalten. Im Fussball werden Anfangsgeschwindigkeiten von über 100 km/h erreicht. Es sind schon Werte bis 183 km/h gemessen worden (David Hirst, September 1996).
Das systemdynamische Modell für den Abstoss besteht aus einer Impulsbilanz für die horizontale und eine für die vertikale Richtung, sowie den beiden Integratoren für den Ort in x-Richtung und in y-Richtung (nach oben). Das Gravitationsfeld entzieht dem Ball mit konstanter Rate Impuls (Gewichtskraft zeigt gegen die y-Richtung). Die Wirkung des Luftwiderstands ist proportional zur Dichte der kinetischen Energie der Anströmung und der Querschnittfläche. Der Einfluss von Form und Oberfläche des Balls wird mit Hilfe des Widerstandsbeiwerts beschrieben. Der Widerstandsbeiwert einer glatten Kugel ist bis zu einer Reynolds-Zahl von etwa 3*105 gleich 0.4 (andere Quellen geben einen Anstieg bis gegen 0.5 an). Danach fällt der Widerstandsbeiwert auf etwa 0.09 (Re = 4*105), um sich danach wieder dem Wert 0.2 zu nähern (Re = 8*106). Der Grund für diesen Einbruch liegt in bei der Querschnittsverringerung der Wirbelstrasse infolge schnelleren Abrisses der Wirbel. Den gleichen Effekt erzeugen die Nähte des Fussballs. Gemäss verschiedener Quellen soll der Widerstandsbeiwert eines Fussballs im Schnitt nur etwa 0.2 betragen.
Die Luft wirkt in beide Richtungen, d.h. zwischen Luft und Ball werden beide Impulskomponenten ausgetauscht. Um die Stärken dieser Impulsströme mathematisch sauber zu formulieren, schreiben wir die Luftwiderstandskraft als Vektor
- [math]\vec F_W=\frac \varrho 2 v^2 c_W A\vec e_v=\frac \varrho 2 v^2 c_W A\frac{\vec v}{v}=\frac \varrho 2 c_W Av\vec v[/math]
Die x-Komponente ist demnach gleich einer Konstanten mal der Betrag der Geschwindigkeit mal die x-Komponente der Geschwindigkeit.
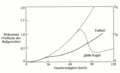
Die ersten drei Bilder zeigen das Systemdiagramm, die Bahnen des Balls unter Variation des Widerstandsbeiwerts (0, 0.2, 0.4) sowie unter Variation des Abschusswinkels (40°, 45° und 50°) bei einer Abschussgeschwindigkeit von 30 m/s (108 km/h). Die Graphik im vierten Bild zeigt den Luftwiderstand in Funktion der Geschwindigkeit für einen Fussball. Im fünften Bild ist die Bahn des Fussballs zu sehen, wobei einmal mit dem Widerstandsbeiwert 0.2 (schwarz), dem gemessenen Luftwiderstand in Funktion der Geschwindigkeit (rot) und mit dem Verhalten einer idealen Kugel (grün) gerechnet worden ist.
-
Systemdiagramm (flowchart)
-
Widerstandsbeiwert 0, 0.2, 0.4
-
Abschuss-Winkel 40°, 45° und 50°
-
Widerstand in Funktion der Geschwindigkeit
-
cW = 0.2 und empirische Kurven
Abstoss mit Rotation
Trifft der Fuss beim Abstoss nicht genau radial auf den Ball, führt er ihm Impuls und Drehimpuls zu. Der Impuls erzwingt die Geschwindigkeit v und der Drehimpuls die Winkelgeschwindigkeit ω des Balls. Infolge der Rotation wirkt auf den Ball neben der Gewichtskraft und dem Luftwiderstand noch eine Magnuskraft. Diese Kraft steht normal zur Geschwindigkeit und normal zur Winkelgeschwindigkeit
- [math]\vec F_M=2\rho c_M V(\vec \omega\times \vec v)[/math]
Die Zahl cM heisst Mangusbeiwert und hängt von der Beschaffenheit des Balls sowie von der Anströmgeschwindigkeit ab.
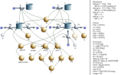
Das erste Bild zeigt das Systemdiagramm (flowchart) zur Berechnung des Abstosses. Im Gegensatz zur Magnusrolle ist hier die Abnahme der Winkelgeschwindigkeit infolge der Luftreibung nicht modelliert. Im zweiten Bild ist die Bahn des Balls mit einer Winkelgeschwindigkeit von 60 s-1 (etwa 10 Umdrehungen pro Sekunde)und verschiedenen Abschusswinkeln dargestellt. Das dritte Bild zeigt die Bahnen bei einem Abschusswinkel von 25° und verschiedenen Winkelgeschwindigkeiten.
-
Systemdiagramm (flowchart)
-
verschiedene Winkel
-
Drallstudie
Bananenflanke
Bei der Bananenflanke fliegt der Fussball auf einer gekrümmten Bahn durch die Luft. Technisch wird die Bananenflanke durch die Rotation des Balls erzeugt. Die Rotation sorgt für eine asymmetrische Umströmung des Balls und damit für eine seitlich wirkende Kraftkomponenten von der Luft auf den Ball (Magnus-Effekt).