Lösungen zu Aviatik 2007/Ass

Aufgabe 1

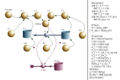
Das erste Bild zeigt das Systemdiagramm und die Gleichungen zur gesamten Aufgabe. Im zweiten Bild ist der Volumenstrom und der Druck in beiden Gefässen bezogen auf einen gemeinsamen Nullpunkt dargestellt. Dieses Problem ist auch geschlossen lösbar. Um die Simulationszeit zu berechnen, rechnet man mit Vorteil die Zeitkonstante aus

[math]\tau=RC[/math] = 4.89 10⁴ s mit [math]C=\frac{C_1C_2}{C_1+C_2}=\frac{A_1A_2}{A_1+A_2}\frac{1}{\varrho g}[/math] = 1.22 10^-6 m³/Pa

• 

  Systemdiagramm

• 

  Volumenstrom und Druck

Aufgabe 2

Eine Kondensator verhält sich im ersten Moment wie ein Kurzschluss und nach langer Zeit wie ein offener Schalter. Die ideale Spule wirkt genau umgekehrt. Deshalb fliesst der Strom im ersten Moment durch R₁ und durch C. Nach langer Zeit geht der Strom durch L und durch R₂.

1. Unmittelbar nach dem Schliessen des Schalters gilt: U₁ = U₀; U₂ = 0;I_L = I₂ = 0; [math]I_C=I_1=\frac{U_0}{R_1}[/math] = 0.25 mA;
2. Längere Zeit danach gilt: U₂ = U₀; U₁ = 0;I_C = I₁ = 0; [math]I_L=I_2=\frac{U_0}{R_2}[/math] = 0.5 mA;
3. Der Energiestrom, der die Spannungsquelle verlässt, geht vollständig in das Widerstandselement 1 hinein und wird dort dissipiert. Die Energiestromstärke ist deshalb gleich der Prozessleistung im Widerstandselement 1: [math]I_W=P=U_1I_1=\frac{U_0^2}{R_1}[/math] = 1.25 mW.

Aufgabe 8

Aufgabe