Aviatik 2009/1

Studiengang Aviatik der ZHAW

Erlaubte Hilfsmittel: Taschenrechner, selbstverfasste Formelsammlung

Daten:

• Gravitationsfeldstärke = 9.81 N/kg
• Dichte von Wasser = 1000 kg/m³

Aufgabe 1

Volumenstrom- und Volumen-Zeit-Diagramm

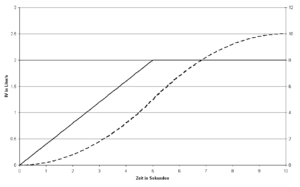
Ein Gefäss besitzt einen Zu- und einen Abfluss. Das Diagramm zeigt den Zufluss (ausgezogene Linie, linke Skala) sowie das gespeicherte Volumen (gestrichelte Linie, rechte Skala) in Funktion der Zeit.

1. Wie viel fliesst in den angegebenen zehn Sekunden in das Gefäss hinein?
2. Wie gross ist die Änderungsrate des gespeicherten Volumens zum Zeitpunkt 5 Sekunden?
3. Wie sieht das Abfluss-Zeit-Diagramm aus? Skizzieren Sie die Form der Kurve und geben Sie passende Eckwerte an.
4. Wie müsste das Abfluss-Zeit-Diagramm aussehen, damit der Inhalt in 10 Sekunden linear von Null auf 10 Liter steigt. Skizzieren Sie die Form der Kurve und geben Sie passende Eckwerte an?

Aufgabe 2

Der Filter einer Gasmaske verhält sich nahezu linear, d.h. die Druckdifferenz nimmt proportional zum Luftstrom zu. Zudem kann die Luft als inkompressibel angesehen werden. Nun zieht ein Proband einen Volumenstrom durch den Filter, dessen Stärke in drei Sekunden linear von Null auf 0.5 Liter/s ansteigt und in weiteren zwei Sekunden wieder linear auf Null abfällt. Die Druckdifferenz steigt dabei bis auf den Maximalwert von 4 kPa an.

1. Wie gross ist die maximal über dem Filter umgesetzte (dissipierte) Leistung?
2. Wie viel Energie wird im Filter während dieser fünf Sekunden umgesetzt (dissipiert)?
3. Wie viel Energie würde umgesetzt, wenn das gleiche Volumen in fünf Sekunden mit konstantem Strom durch den Filter geleitet würde?
4. Berechnen Sie für beide Prozesse (für den Prozess in 1. und 2. mit linear ansteigendem und wieder fallendem Volumenstrom sowie für den Prozess in 3. mit konstantem Volumenstrom) die mittlere Leistung.

Aufgabe 3

Eine Pumpe fördert unabhängig von der Druckdifferenz einen konstanten Volumenstrom von 180 l/min (3 l/s). Lässt man diesen Strom durch einen ersten Filter (A) fliessen, misst man eine Druckdifferenz von 4.2 bar. Beim zweiten Filter (B) beträgt die Druckdifferenz nur 1.8 bar. Die Strömung ist laminar in allen Fällen von 1. bis 4.

1. Wie gross sind die hydraulischen Widerstände von Filter A und B?
2. Welchen Widerstand setzen die beiden Filter gemeinsam dem Volumenstrom entgegen, wenn dieser nacheinander durch beide Filter fliesst (Serieschaltung)? Wie gross ist der Widerstand, wenn der Strom sich aufteilt und gleichzeitig durch beide Filter fliesst (Parallelschaltung)?
3. Wie gross ist die dissipierte Prozessleistung beim kleineren Widerstand in der Serieschaltung?
4. Wie gross ist die dissipierte Prozessleistung beim kleineren Widerstand in der Parallelschaltung?

Aufgabe 4

Das Diagramm zeigt das Druck-Volumen-Diagramm eines Speichers. Nun werde der leere Speicher mit einem konstanten Volumenstrom beladen.

1. Wie stark muss der Volumenstrom sein, damit der anfangs leere Speicher in 75 Sekunden mit 25 Liter gefüllt ist.
2. Wie stark ist der dem Volumenstrom zugeordnete Energiestrom 30 Sekunden nach Beginn des Füllvorganges?
3. Wie viel Energie wird dem Speicher total, d.h. in 75 Sekunden zugeführt?
4. Obwohl sich der Speicher nichtlinear verhält, kann man ihm bei einem bestimmten Füllzustand eine Kapazität zuweisen. Wie gross ist die Kapazität bei 20 Liter gespeicherter Flüssigkeit?

Aufgabe 5

Ein zylinderförmiger Topf ist anfänglich ein Meter hoch mit Quecksilber (Dichte 13’500 kg/m³) gefüllt. Nach dem schnellen Öffnen des Abflusses strömt das Quecksilber durch ein horizontales Rohr (Länge 2 m) in eine Auffangwanne weg.

1. Wie gross ist die Querschnittsfläche des zylinderförmigen Topfs?
2. Berechnen Sie den Faktor k der turbulenten Strömung mit Hilfe des Diagramms?
3. Berechnen Sie mit Hilfe des Diagramms die Änderungsrate des Volumenstroms zum Zeitpunkt 0 Sekunden.
4. Bestimmen Sie die hydraulische Induktivität des Rohres.

Lösung zu Aviatik 2009/1