Carnot-Prozess

Geschichte

Nicolas Léonard Sadi Carnot (*1. Juni 1796 in Paris; †24. August 1832 in Paris) hat in seiner berühmten Arbeit "Réflexions sur la puissance motrice du feu" einen theoretischen Prozess eingeführt, um die von einer Dampfmaschine maximal freisetzbare Energie abzuschätzen. Carnot argumentiert mit einem Wärmestoff (calorique), der wie das Wasser im Wasserfall von einem hohen zu einem tiefen Nivau (Temperatur) fällt und dabei bewegende Kraft (puissance motrice) freisetzt:

"Die bewegende Kraft des fallenden Wassers hängt von seiner Höhe und der Menge der Flüssigkeit ab; die bewegende Kraft der Wärme hängt gleichfalls von der Menge des angewendeten Wärmestoffes ab, und dem, was man seine Fallhöhe nennen könnte, und was wir in der That so nennen wollen, nämlich den Temperaturunterschied der Körper, zwischen denen der Austausch des Wärmestoffes stattfindet."

Heute wissen wir, dass Carnot mit Wärmestoff die Entropie und mit bewegender Kraft die Energie gemeint hat. Der eigentliche Carnot-Prozess (Carnot-Zyklus) verläuft zwischen zwei Wärmespeichern unterschiedlicher Temperatur und wird mit einem idealen Gas geführt. Doch lassen wir den Meister seinen Prozess selber erklären:

Skizze nach Sadi Carnot

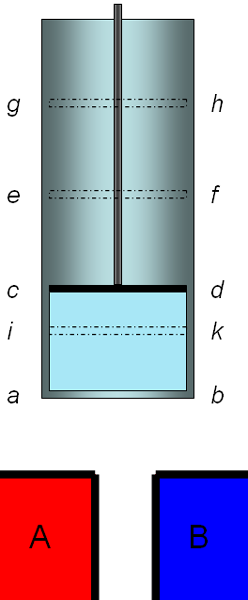
"Nachdem diese vorläufigen Punkte festgestellt worden sind, denken wir uns eine elastische Flüssigkeit, z.B. atmosphärische Luft in einem cylindrischen Gefäss abcd, mit einer beweglichen Scheidewand oder einem Kolben cd enthalten; wir denken uns ferner zwei Körper A und B, von denen jeder bei einer constanten Temperatur erhalten wird, wobei die von A höher sei, als die von B; wir stellen uns nun die nachstehend beschriebenen Reihe von Operationen vor.

1. Berührung des Körpers A mit der im Raum abcd enthaltenen Luft, oder mit der Wandung dieses Raumes, von welcher wir annehmen, dass sie die Wärme leicht durchlässt. Die Luft befindet sich vermöge dieser Berührung bei der Temperatur des Körpers A; cd sei die augenblickliche Stellung des Kolbens.
2. Der Kolben erhebt sich stetig und nimmt die Stellung ef ein. Zwischen dem Körper A und der Luft bleibt fortwährend Berührung bestehen, wodurch die Luft während der Ausdehnung bei constanter Temperatur erhalten wird. Der Körper A liefert den nöthigen Wärmestoff, um die Temperatur constant zu halten.
3. Der Körper A wird entfernt und die Luft befindet sich nicht mehr in Berührung mit einem Körper, welcher ihr Wärmestoff liefern kann; der Kolben setzt indessen seine Bewegung fort und geht aus der Stellung ef in die Stellung gh. Die Luft wird verdünnt, ohne Wärmestoff aufzunehmen, und ihre Temperatur sinkt. Wir nehmen an, dass sie bis zu der des Körpers B sinkt; in diesem Augenblick bleibt der Kolben stehen und befindet sich in gh.
4. Die Luft wird nun in Berührung mit dem Körper B gesetzt; sie wird durch Senkung des Kolbens weiter comprimirt, indem man ihn aus der Stellung gh in die Stellung cd bringt. Dabei bleibt die Luft aber bei constanter Temperatur, weil sie den Körper B berührt, dem sie ihren Wärmestoff abgibt.
5. Nachdem der Körper B entfernt ist, setzt man die Compression der Luft fort, welche in ihrem isolierten Zustande eine Temperaturerhöhung erfährt; die Compression wird fortgesetzt, bs die Luft die Temperatur des Körpers A angenommen hat. Der Kolben bewegt sich während dieser Zeit aus der Stellung cd in die Stellung ik.
6. Die Luft wird mit dem Körper A in Berührung gebracht; der Kolben kehrt aus der Lage ik in die Lage ef zurück; die Temperatur bleibt unverändert.
7. Die unter 3. beschriebene Periode wiederholt sich, sodann die Perioden 4, 5, 6, 3, 4, 5, 6, 3, 4, 5 u.s.w.

Theorie

Setzt man den Wärmestoff von Carnot mit der Entropie und die treibende Kraft mit der Energie gleich, hat Carnot schon alles gesagt, was es zu sagen gibt. Die sechs Punkte von Carnot lassen sich auf vier Teilprozesse reduzieren:

1. isotherme Expansion: das Gas bläht sich auf und übernimmt eine ganz bestimmte Menge Entropie vom Körper A. Weil das Gas die gleiche Temperatur wie der Körper A aufweist, wird keine zusätzliche Entropie erzeugt. Die von der Entropie mitgeführte Energie ist gleich Entropie mal Temperatur (Menge mal Beladungsmass). Diese Energie wird direkt in Form von mechanischer Arbeit über die Kolbenstange an die Umgebung abgegeben. Die innere Energie des Gases bleibt konstant.
2. isentrope Expansion: das Gas dehnt sich ohne Entropiezufuhr weiter aus. Weil die Entropie eines Gases bei konstanter Temperatur mit dem Volumen zunehmen müsste, kühlt sich das Gas ab: das Gas formt akute (temperaturwirksame) Entropie in latente (nicht temperaturwirksame) Entropie um. Zudem gibt das Gas einen Teil seiner inneren Energie in Form von Arbeit an die Umgebung ab.
3. isotherme Kompression: das Gas wird zusammengedrückt und gibt die vom Körper A übernommene Entropie an den Körper B weiter. Weil das Gas die gleiche Temperatur wie der Körper B aufweist, wird keine zusätzliche Entropie erzeugt. Die von der Entropie weggeführte Energie ist wieder gleich Entropie mal Temperatur. Weil die Temperatur von Körper B kleiner als von Körper A ist, führt die Entropie weniger Energie an B ab, als sie im Prozess 1 vom Körper A ins Gas hinein geschleppt hat. Weil die innere Energie des Gases konstant bleibt, muss die von der Entropie weggetragene Energie in Form von mechanischer Arbeit über die Kolbenstange zugeführt werden.
4. isentrope Kompression: das Gas wird ohne Entropiezufuhr weiter zusammengedrückt. Die Entropie wird thermisch hochgequetscht, das Gas formt latente (nicht temperaturwirksame) Entropie in akute (temperaturwirksame) Entropie um. Die dazu notwendige Energie wird dem Gas über die Kolbenstange zugeführt. Folglich nimmt die innere Energie des Gases zu.

Weil das Gas gleich viel Entropie an den Körper B abgibt, wie es vom Körper A übernommen hat, hat es am Schluss bei gleichem Temperatur wieder das gleiche Volumen wie zu Beginn des Kreisprozesses.

Modell

Simulationsergebnisse

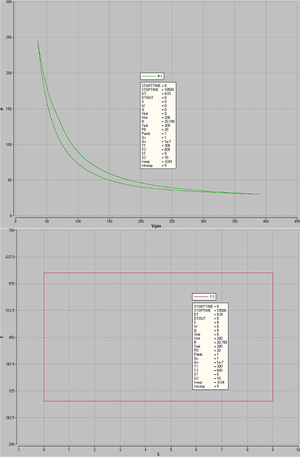
Der Carnot-Zyklus kann mit Hilfe des Carnotors nachmodelliert werden. Dazu schaltet man zwei isotherme und zwei isentropen Prozesse in der richtigen Reihenfolge in Serie. In den beiden isothermen Prozessen muss entgegengesetzt gleich viel Entropie mit den entsprechenden Wärmebäder ausgetauscht werden. Die isentropen Prozesse sind durch die beiden Temperaturen im wesentlichen festgelegt.

Die beiden isentropen Prozesse sind mit Hilfe eines aufgeprägten Volumenstromes einfach zu modellieren. Bei den isothermen Prozessen wird der Entropiestrom über den Leitwert und die angelegte Temperaturdifferenz gesteuert. Ist der Leitwert zu klein, verläuft der Temperaturausgleich zu langsam und der Prozess zu wenig isotherm. Wählt man den Leitwert zu gross, können numerische Probleme auftauchen.

Die nebenstehende Skizze zeigt das p-V- und das T-S-Diagramm eines Carnot-Kreisprozesses mit dem idealen Gas, der von den Studierenden des Studienganges Informationstechnologie der ZHW mit Hilfe des Carnotors simuliert worden ist.

Video

<videoflash>4xZsZaDHwg0|640|360</videoflash>

Links

• Animation des Carnot-Prozess
• Carnot-Zyklus auf Youtube